站起來的兒童數學教育

莊惠芬

摘要：兒童作為完整的人，在學校應該享受完整的教育。“站起來的兒童數學教育”這一主張以馬克思關于人的全面發展學說、杜威的做中學等理論為依據，努力種一棵“兒童數學”之樹，其根為兒童數學的真善美，其干為兒童，其三個主要枝條為站起來的兒童數學學習、站起來的兒童數學教學、站起來的兒童數學課程。

關鍵詞：站起來的兒童數學教育;教育主張;童本課堂教學模式

中圖分類號：G42 文獻標志碼：A 文章編號：1673-9094（2015）06A-0018-05

迄今為止，兒童的成長密碼還遠沒有被我們成人完全發現。在兒童數學學習的路上，我們需要從對“群體兒童”的控制走向對“個體兒童”的關注，從對“應然兒童”的假設走向對“實然兒童”的思考，從“發展兒童”走向“兒童發展”。在我看來，兒童首先是“玩童”。玩是兒童的天性，玩是兒童的興趣所在，這意味著兒童的數學學習是伴隨著做、學、玩合一的過程。其次，兒童是“丸童”。雖然他們個小，但能量很大，這意味著我們要去發現兒童的無限潛能。再次，兒童是“完童”。兒童作為完整的人，在學校應該享受完整的教育，這意味著我們要為兒童提供全面發展的教育。于是我提出了“站起來的兒童數學教育”這一主張。

在我看來，站起來的兒童數學教育其根猶如一只鼎，支撐這只鼎的三足是數學之真、數學之善、數學之美。數學之真在于讓兒童求真，在數學學習中學會理性地思維、客觀地看問題;數學之善在于臻善，在數學學習中養成實事求是、一絲不茍的數學精神;數學之美在于尚美，在數學學習中體驗簡潔明了、和諧美好的數學文化。站起來的兒童數學教育就是要讓兒童獲得這“三足”，給孩子找到支點、找到支撐，讓兒童自如地行走、自由地奔跑、自主地建構。

一、理論依據

我提出“站起來的兒童數學教育”這一主張，主要有以下四個理論依據。

（一）馬克思主義關于人的全面發展學說

馬克思認為人的發展是全面的發展，提出了“個人的全面發展”、“全面發展的個人”、“個人獨創的和自由的發展”等概念。馬克思、恩格斯指出：“每個人的自由發展是一切人的自由發展的條件。”[1]要達到個人充分的全面自由發展，只能是通過實踐，而且只有在個人本身獲得能夠自由駕馭外部世界的力量的時候才能實現。站起來的兒童數學教育，注重動腦、動手、動口，注重兒童心靈的舒展，強調兒童自由而又主動的發展。

（二）杜威的“兒童中心論”與“做中學”

杜威認為，兒童是教育的出發點，學校生活組織應該以兒童為中心，使得一切主要是為兒童的而不是為教師的。他提倡“從做中學”，認為教學要從兒童的現實生活出發，并且附著于兒童的現實生活。在課程選擇上，他提議：“學校科目的互相聯系的真正中心，不是科學，不是文學……而是兒童本身的社會活動。”[2]站起來的兒童數學教育，真正以兒童為中心，尊重兒童、理解兒童、發現兒童，讓兒童在做中學、學中思、思中創，在此過程中不斷成長。

（三）皮亞杰的認知發展理論

皮亞杰認為智力源于動作，強調操作在掌握數學概念、原理中的作用。他認為隨著兒童年齡的增長，其認知發展涉及到圖式、同化、順應和平衡四個方面，數學學習過程是學生的數學認知結構能力的建構過程，兒童的數學世界、兒童的數學生活、兒童的心靈成長都是按照發展階段的嚴格順序發生數次結構性轉變的。

（四）弗賴登塔爾對現實問題的數學化與“再創造”學習

弗賴登塔爾認為，情景問題是教學的平臺，數學化是數學教育的目的，學生通過自己的努力得到的結論和創造是教育內容的一部分，“互動”是主要的學習方式，學科交織是數學教育內容的呈現方式。兒童學習數學就是一個將現實問題抽象為數學問題，讓兒童經歷再創造的過程。站起來的兒童數學教育注重做、學、玩合一，思、創、行一體，在數學學習中不斷經歷再創造的過程，不斷建構起自己的數學世界。

二、基本原理

“站起來的兒童數學教育”之“站起來”，是對兒童生命成長規律的把握，是對兒童數學學習特點的理解，是對兒童數學教育原理的建構。“站起來的兒童數學教育”不僅從哲學上找到依據，而且還借鑒心理學、數學教育學等研究成果，構成“站起來的兒童數學教育”的基本原理。

（一）數學建模原理

數學即模型，數學建模就是讓兒童經歷問題情境—發現問題—建立模型—檢驗—解釋、應用與拓展的過程（如圖所示），把現實世界中的實際問題加以提煉，抽象為數學模型。在這個過程中，讓兒童獲得概念模型、方法模型、結構模型等等。“站起來的兒童數學教育”抓住模型思想，就是抓住了數學的建構，就能夠高屋建瓴，鳥瞰數學，深入實際，開辟一條對數學、對兒童學數學本質把握的兒童數學教育的新路徑。

（二）自我建構原理

“站起來的兒童數學教育”關注兒童的內在價值，強調兒童主體存在，從而建構兒童完滿人格。站起來的兒童數學教育，為不同個性、不同水平的兒童提供相應的思維場，讓兒童在數學觀察、積極嘗試、發現問題、大膽猜測、主動驗證、得出結論的過程中自主建構，讓兒童通過不同的方式發現問題、探索數學、體驗成功。

（三）全腦思維原理

人腦包括左右兩側半球。一般來說，左腦的主要功能是言語、書寫、分析、邏輯推理、數學運算、抽象思維、形成概念等，具有連續性、有序性、分析性的特點。右腦的主要功能有空間方位辨別、幾何圖形識別、形象思維、開展創造性和綜合性活動等，具有連續性、彌漫性、整體性的特點。兒童數學學習的過程需要直觀形象，也需要邏輯抽象，需要二者很好地結合。

（四）情理交融原理

數學是情趣與理趣的交融。如果數學缺失了情感，她就只是冷冰冰的知識體系;如果教學缺少了情感，就沒有想象、發現、創造和美感。我追求“融情于理，融情于智，潤澤生命”的兒童數學，是基于兒童的認知特點和學科特性，把師生的情緒、情感、情意、情趣融進數學的學習中。真摯的情感會深深融入到兒童的內心世界，更好地促進兒童的成長。

三、實踐建構

我們在努力種一棵叫做“兒童數學”的樹，這棵“站起來的兒童數學之樹”，其根為兒童數學的真善美，其干為兒童，其三根主要枝條為站起來的兒童數學學習、站起來的兒童數學教學、站起來的兒童數學課程。

（一）主體立場，站起來的兒童數學學習

1.以兒童的學為起點

起始之點。教學從哪里開始？奧蘇伯爾認為，影響學習的最重要原因是學生已經知道了什么，我們應當根據學生已有的知識水平進行教學。在我看來，教師要善于從認知起點、思維起點、情感起點這三個維度把握兒童學習數學的錨樁。從知識體系的維度把握認知起點，在兒童思維發展的維度把握思維起點，在兒童數學學習的情趣中把握情感起點，尋找兒童數學學習的“最近發展區”與“最優發展區”，在兒童愿意學、善于學、主動學中開啟數學學習之門。

預習之理。真正意義上的預習在數學教學中有著獨特的價值。兒童需要預習嗎？兒童能夠預習嗎？兒童喜歡預習嗎？在預習中我們需要給兒童有效的指導，如指導學生預習提綱、做好預習筆記、設計預習菜單。在預習的基礎上如何展開教學，這更是值得重視的。兒童“看得懂”的，教師就作“點接”;兒童“說不透”的，教師就作“點撥”;兒童“道得明”的，教師就作“點化”;兒童“寫得出”的，教師就作“點評”。

游戲之魅。游戲，不僅僅是課始敲門磚，不僅僅是課堂調味品，也不僅僅是低年級的專利。我們要追尋數學游戲的內在品質。數學游戲是生命成長的動力源，是學科發展的加油站，是數學研究的孵化地。在教學中構造數學游戲的中間地帶，讓游戲和數學情趣自由徜徉，讓游戲與數學思想相互碰撞，讓游戲和數學精神深刻共鳴。

同理之心。站起來的兒童數學學習需要同理之心。同理心就是在彼此交往中能比較正確地了解他人的感受、情緒和境地，在情感上給予理解、關懷和幫助，從而形成彼此的認同與心理的融洽。兒童在數學學習的過程中，不是簡單地帶著理性的軀殼進入冰冷的數學文本的，他必定是帶著自己已有的認知基礎、思維方式、情感態度走入學習場的。教師要走進學生心靈，了解他們真正的內心需求，嘗試適合他們的教學手段，尋找他們感興趣的學習內容，探究適合他們的學習方法，促進他們的自我成長。

2.以兒童的思維發展為核心

在多年的數學教學中，從一年級到六年級，我們在兒童形象思維能力與邏輯思維能力的培育方面做了很多嘗試。我們還從不同的層面去關注系統思維、圖構思維、非邏輯思維、批判性思維、辯證思維等的價值與作用。

系統思維。培養兒童的系統思維，是為了讓兒童有開闊的數學視野，面對問題能整體分析、全面思考，能對解決問題的方法與策略進行綜合優化，使兒童的數學學習不再局限在點滴的散狀的知識中，不再停留在亦步亦趨的方法模仿中。

圖構思維。德國數學家克萊因認為，數學的直觀就是對概念、證明的直接把握。通過形對數的描述、數對形的表達，數與形的不斷結合、不斷構造，促進兒童對數學問題的直接洞察，充分發揮圖構在兒童思維生長中的作用。借助諸如直觀形象圖、數學概念圖、邏輯思維圖、數量關系圖、知識網絡圖等，可以促進兒童對數學問題的理解與分析;依托數與形的結合，可以讓兒童真正理解數學概念、發現數學規律、獲得數學方法、擁有數學思想，從而促進兒童數學素養的提升。

批判性思維。培養學生的批判性思維，使學生學會“批判”，是一個漸進的過程，需要通過環境營造、障礙消除、語言激勵、角色互換等培養批判意識。通過反例法、反證法、排除法、比較法等，嘗試客觀批判，貫徹一分為二的思想，恰如其分地表達。

非邏輯思維。非邏輯思維是相對于邏輯思維而言的，它也屬于科學思維的范疇。非邏輯思維主要是根據情境和所提供的各種相關信息進行獨特而綜合性的思維，它不受程式化的程序束縛，不受固化的邏輯規則的約束。兒童在具體場景中產生靈感思維、直覺思維和頓悟思維，綻放出創新的火花。

辯證思維。數學是一門理性的學科。兒童在數學學習的過程中，需要實事求是、客觀理性、一分為二地看待問題，需要從不同的角度關注問題，需要通過動手做去解決問題，一、二、三年級是兒童辯證思維的啟蒙期，四年級是辯證思維發展的轉折期，五六年級是辯證思維的發展期。教師要挖掘數學學習內容中辯證思維的要素，逐步提高兒童的“辯證思維”水平。

（二）整體把握，站起來的兒童數學教學

1.用三個層面研讀教材

一是用結構的方式研讀知識體系。從兒童認知結構的形成、發展規律，站在數學知識體系的整體角度，把握、理解和處理教材，讓兒童感受知識的來龍去脈，從中感受數學的知識結構、方法結構。二是從核心知識的角度研讀內容維度。對每一項數學學習內容，從數學模型這個核心角度把握數學的思想精神、數學的思維方法和看問題的著眼點。三是從兒童的角度理解教材，尊重兒童的學習需求，把握思維的梯度，從為教而教走向為學而教、為人而教，讓兒童徜徉于充滿樂趣的數學之旅。

2.構建童本課堂模式

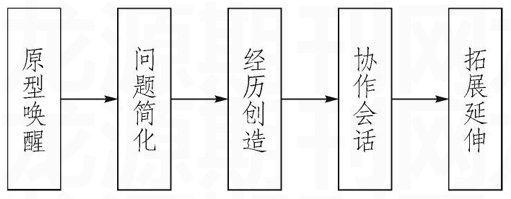
童本課堂特點：問題導向、自主探索、體驗創造、立足素養，真正讓兒童做學玩合一、思創行一體。所形成的基本的教學模式為（如下圖所示）：

“原型喚醒”，讓兒童親身體驗生活，從生活原型中找到數學模型，主動獲取真實信息。

“問題簡化”，以問題為導向，讓兒童從紛繁復雜的具體情境中發現問題，抽象出數學問題。

“經歷創造”，讓兒童的數學學習經歷再創造的過程，經歷問題的發現、規律的探索、模型的建立等過程。

“協作會話”，主要通過兒童、文本、教師三者之間的有效協作，體悟數學之美，為兒童合理建模奠定基礎，在兒童的世界里共生。

“拓展延伸”，通過尋找知識與兒童生活的最佳結合點，豐富兒童心智，完善兒童人格，獲得數學之善。

童本課堂的六個支架：一是融情于理與融情于智、理趣與情趣融合的教學風格;二是思維訓練與思想滲透、形式與本質相統一的學習過程;三是線性教學與版塊教學、條狀與塊狀相協調的課堂結構;四是模型結構與自我建構、協同與自主相結合的目標指向;五是發展兒童與兒童發展、主導與主體相結合的教學策略;六是做學玩與思創行一體、數量關系與空間形式的融合。

3.把握兒童數學學習的三個關鍵期

“心理敏感期”，幼小數學學習的過渡。把握從幼兒園升入小學的兒童的認知階段性——從口頭語言發展到書面語言，從直覺行動思維轉變為具體活動，從游戲活動轉變到掌握間接經驗活動。把握目標的連續性，通過兒童自身的活動對客觀世界中的數量關系和空間形式進行感知、操作、發現、探究，獲得感性經驗。把握時間的彈性化，通過游戲與實物操作學習，彈性地調整一年級兒童的上課時間，通過動靜交錯的教學方式，維持課程內容的相關性與延續性。

“成長馬鞍期”，中年級數學學習的適應。三四年級是兒童的“成長馬鞍期”，這時的數學學習對于有些孩子來說是成長中的“一道坎”。有近十分之一到四分之一的兒童存在學習適應性差的問題，出現對學習的焦慮和恐懼等狀態。在兒童數學學習中，教師要通過豐富的情境遷移，喚起兒童積極的認知;通過積極的心理暗示，讓兒童不斷激發對自我的認同;通過內容適度調試，注重學習內容與認知方式的匹配;注重爬坡而行，減少數學的兩級分化。

“學習斷層期”，中小學數學學習的銜接。雖然數學課程標準是九年一個整體編制，但是無論是教材編寫還是教學的展開都是各自為政，所以兒童的數學學習從六年級到初中會產生明顯的斷層期。教師要注重課程目標、課程內容、課堂教與學方式的漸次變化，注重兒童數學學習習慣、思維方式、學習心理、學習強度的漸長適應，通過知識、經驗、思維、思想上的銜接，為學生的可持續學習奠定基礎。

（三）立體構建，站起來的兒童數學課程

1.課程目標的把握

以核心素養作為課程目標的旨歸，以抽象概括、數學建模、幾何直觀、推理、運算能力等兒童數學核心素養為課程目標的支點，讓兒童用數學的感覺體驗社會，無限逼近數感;用數學的視角理解生活，形成數學符號意識;用數學的技能表達生活，培養數學運算能力;用數學的方法解決問題，提升問題解決能力;用數學的聯系構造世界，發展數學空間觀念;用數學的方式思考問題，培養數學推理能力等等。

2.課程內容的完善

進行教材、學材、習材為維度的三材開發，豐富對兒童數學課程的理解。教材的解讀：通過對不同版本教材的解讀，汲取其共同的邏輯線索與數學文化，把教材讀厚，同時又加進自己不同的設計理念與思維方式，把教材讀透，把理想的課程變成現實的課程;學材的開發：從數學與美學、數學與歷史、數學與體育、數學與藝術等方面將數學的理性之美與數學文化之善對接，通過專題式的探索，讓兒童獲得數學力量;習材的編寫：從綠色套餐、銀色套餐、金色套餐的習材編寫，讓不同的孩子在學習中有不同層次的選擇。

3.課程形態的豐富

通過學校數學課程情境分析、學校課程建構的需求調研，構建“一體三翼、四輪驅動”的課程體系：“一體”指站起來的兒童數學教育;“三翼”指國本課程（教材）的校本化、校本課程（學材）的個性化、生本課程（習材）的人性化;“四輪”指必修與選修、顯性與隱性、共性和個性、國本與生本，形成多元開放的課程體系。

站起來的兒童數學教育，彌散著的是一種育人情懷。站起來的兒童數學教育，目標是育人，即為了人的全面、和諧、可持續的發展。站起來的兒童數學教育，是一種本質的自然回歸，體現的是一種本真的價值追求。站起來的兒童數學教育，是一種不斷豐富的教育形態，是教師思維方式、育人模式的超越。

參考文獻：

[1]周為民.馬克思主義關于人的學說[M].北京：人民出版社，2011：294.

[2]約翰·杜威.學校與社會：明日之學校[M].趙祥麟，任鐘印，吳志宏，譯.北京：人民教育出版社，2005：3.

責任編輯：丁偉紅

Standing-up Mathematics Education for Children

ZHUANG Hui-fen

（Wujin Xinghe Primary School， Changzhou 213161， China）

Abstract： Children， as whole humans， should receive the whole education in school. Standing-up mathematics education for children is based on the doctrine of Marx on humans all-round development and Deweys theory on learning by doing， striving to plant a tree of children mathematics， whose root is childrens truth， goodness and beauty， whose trunk is children themselves， whose three main branches are standing-up children mathematics learning， teaching， and mathematics curriculum.

Keywords： standing-up mathematics education for children; education view; child-based classroom teaching mode