彈性支承梁固有頻率影響因素研究*
馬晨光,劉昌洪,陳曉嵐
(北京電子工程總體研究所,北京 100854)
彈性支承梁固有頻率影響因素研究*
馬晨光,劉昌洪,陳曉嵐
(北京電子工程總體研究所,北京 100854)
通過將折疊舵簡化為梁模型來研究一種典型結(jié)構(gòu)折疊舵頻率的影響因素。對于梁內(nèi)出現(xiàn)的彈性支承情形,采用了以分段表示的運動微分方程、簡支和自由邊界條件以及彈性支承處連續(xù)性條件來描述。根據(jù)梁的振動的基本方程,推導(dǎo)出彈性支承彎曲振動梁的頻率方程的解析表達式,并利用數(shù)值方法計算出在不同條件下彎曲振動梁的頻率,研究彈簧剛度,有效比剛度,以及支承點位置對固有頻率的影響。
彈性支承;振動方程;彈簧剛度;比剛度;支承位置
0 引言
現(xiàn)代防空導(dǎo)彈為了提高作戰(zhàn)單元的火力密度,減小發(fā)射筒(或箱)的外形尺寸,一般采用折疊舵面,折疊舵面與舵軸通常為鉸鏈連接,并通過一定的展開機構(gòu)來驅(qū)動。導(dǎo)彈的折疊空氣舵由于折疊間隙的影響使空氣舵的彎曲頻率大幅度下降,進而容易引發(fā)顫振問題,導(dǎo)致飛行試驗失敗,目前該問題已成為折疊舵結(jié)構(gòu)設(shè)計的瓶頸。本文通過將折疊舵簡化為梁模型,研究不同因素對梁模型振動頻率的影響。
國內(nèi)外學(xué)者已經(jīng)推導(dǎo)出在基本邊界條件(兩端簡支、兩端固定、懸臂梁)下等截面直梁的彎曲振動頻率方程[1-2],并且對其進行了詳細的分析,得出梁在彎曲振動時的固有頻率會因為邊界條件的不同而不同。
楊曉東等[3]研究了帶有扭轉(zhuǎn)彈簧支承梁的固有特性,宋殿義等[4]研究了兩端線性彈簧支承梁的自振頻率,并分析彈性支承剛度對頻率的影響,馬連生等[5]研究了不同梁理論之間簡支梁特征值的解析關(guān)系。
本文以具有彈性支承的彈性梁的問題為例,具體分析了彈性支承的彈性系數(shù)、支承位置和材料有效比剛度對梁的振動頻率和穩(wěn)定性的影響。
1 折疊舵模型的簡化
現(xiàn)代防空導(dǎo)彈一般采用折疊舵面,舵面與舵軸通常為鉸鏈連接,連接部分的剛度為舵面固有頻率的重要影響因素。一種典型的折疊舵結(jié)構(gòu)如圖1所示。
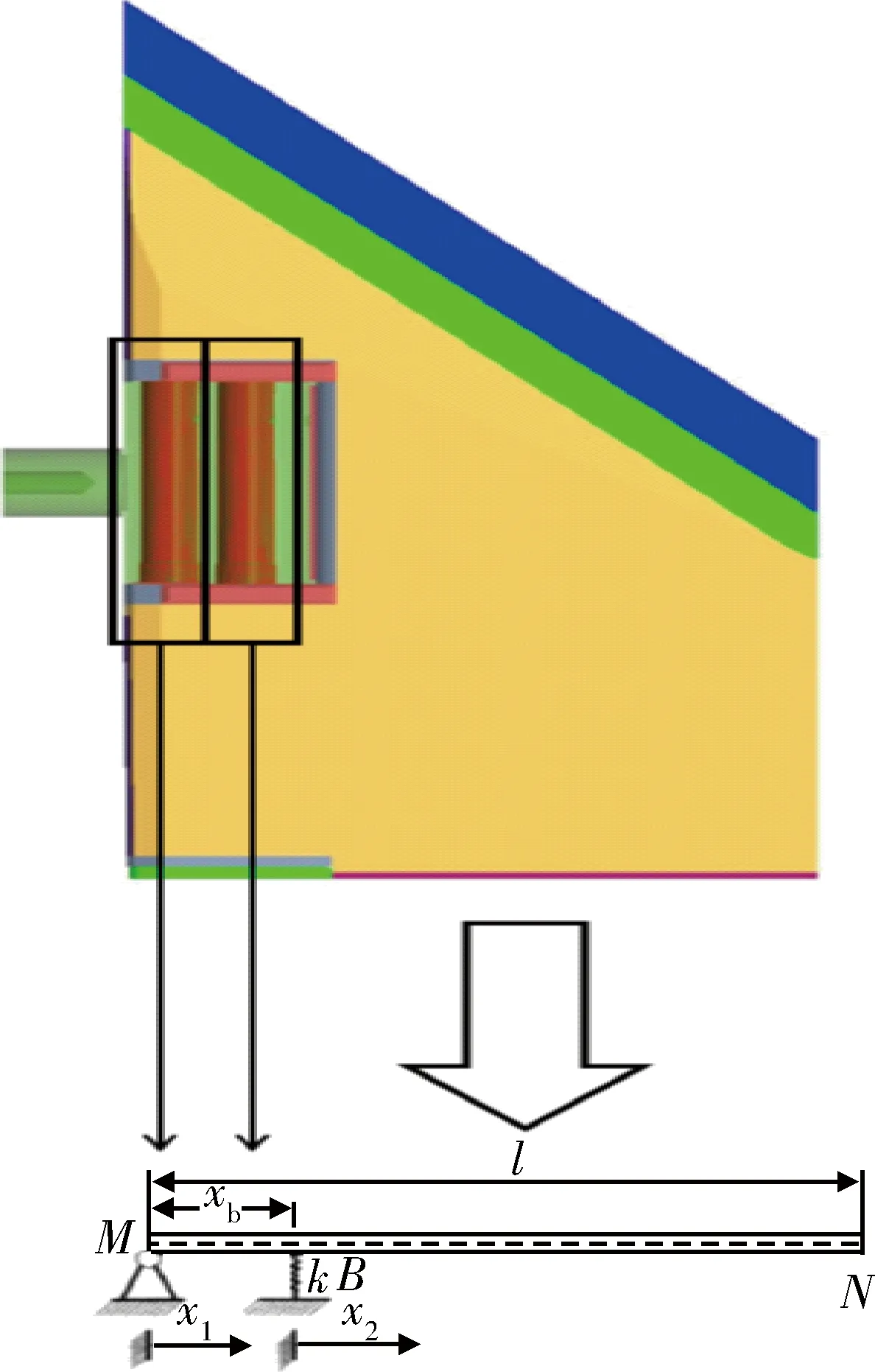
圖1 舵面簡化為梁模型Fig.1 Simplify the folding rudder into a beam
將舵面簡化為梁過程如下:轉(zhuǎn)軸處連接剛度是非線性的,為了便于研究,將2根轉(zhuǎn)軸分別視為簡支和彈性支承,支撐點位置xb對應(yīng)折疊舵兩轉(zhuǎn)軸距離;彈簧彈性系數(shù)k對應(yīng)折疊舵兩轉(zhuǎn)軸的連接剛度;主要研究上述因素對彎曲頻率的影響。
2 梁的頻率方程推導(dǎo)
如圖2所示,具有彈性支承的等截面直梁,密度為ρ,截面彎曲剛度為EI,長度為l,左端M處為簡支,右端N處為自由端,B處為彈性支承,彈簧彈性系數(shù)為k。
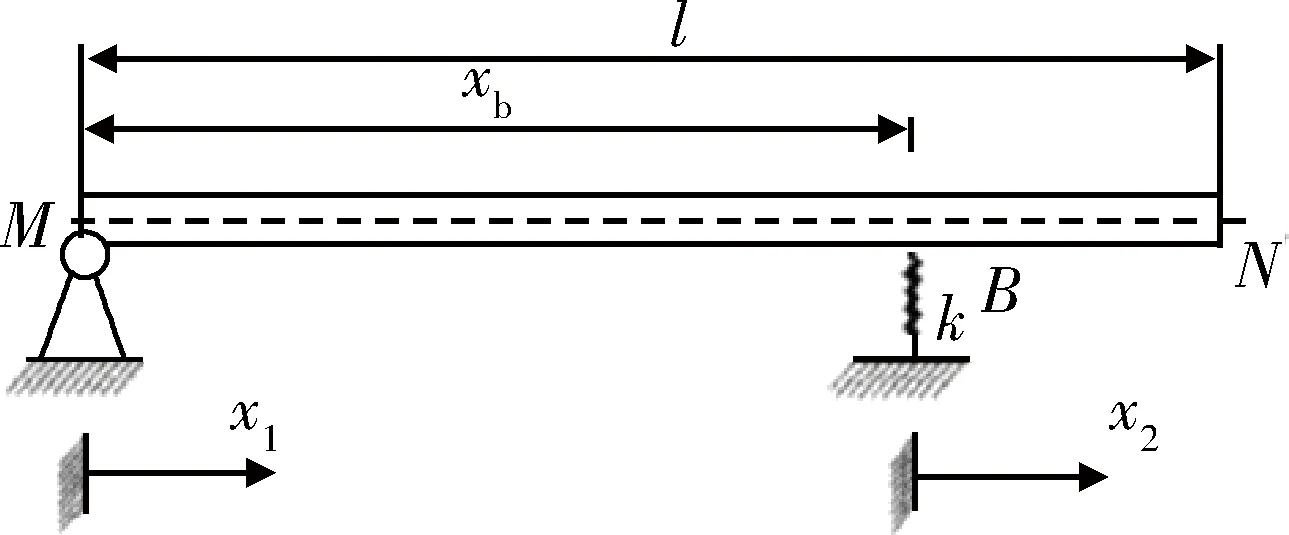
圖2 帶彈性支承的簡支梁Fig.2 Simply supported elastic beams with internal elastic supports
目前,一些學(xué)者對含有彈性支承的梁的振動和穩(wěn)定性問題的研究中,一般采用把彈性支承處的約束力用廣義Dirac-delta函數(shù)表示為連續(xù)分布力[6-7],這樣,運動微分方程中將出現(xiàn)多個δ函數(shù),然后用積分方程法求解。例如XU M[8-9]等采用積分方程法研究了具有彈性支承彈性梁的自由振動和具有彈性支承的矩形板的自由振動問題;趙鳳群等[10]分析了在切向均布隨從力作用下含有彈性支承的非保守彈性矩形板的穩(wěn)定性問題。
雖然積分方程法能有效地求解微分方程中含有多個δ函數(shù)的問題,但若方程中同時包含函數(shù)的偶數(shù)和奇數(shù)階導(dǎo)數(shù),或邊界條件不是簡支時,用積分方程法求解就有困難。本文建立了分段表示的運動微分方程[11],將支承的作用看成連續(xù)性條件,這樣方程中將不出現(xiàn)δ函數(shù)。
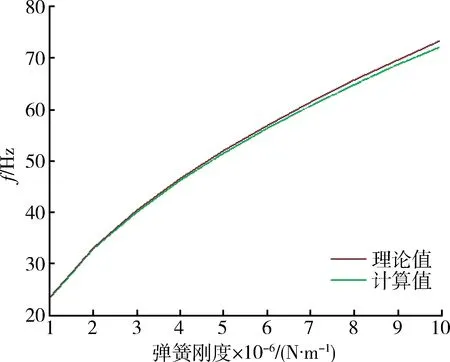
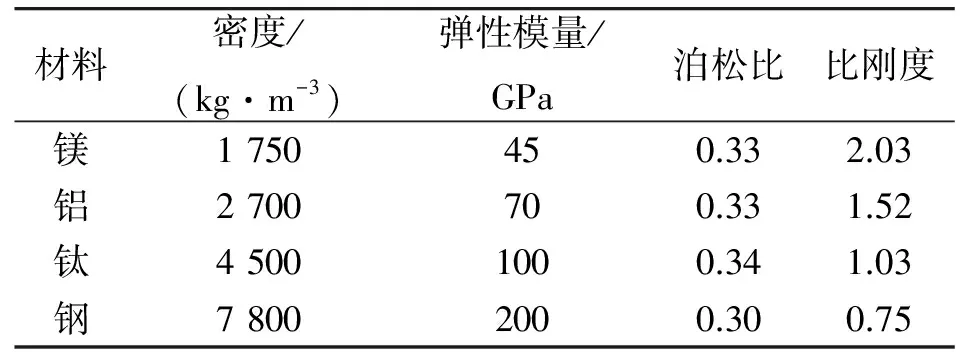
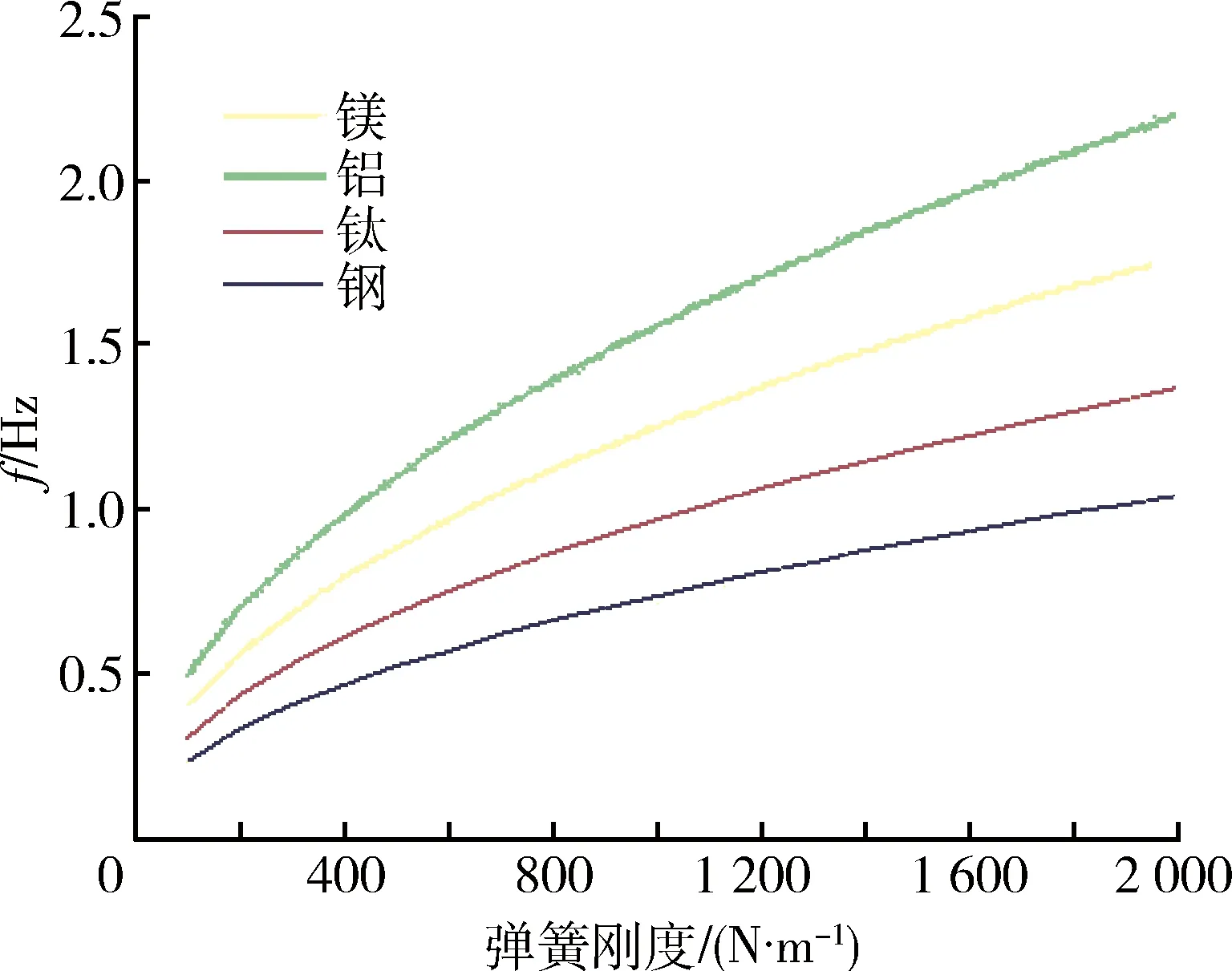
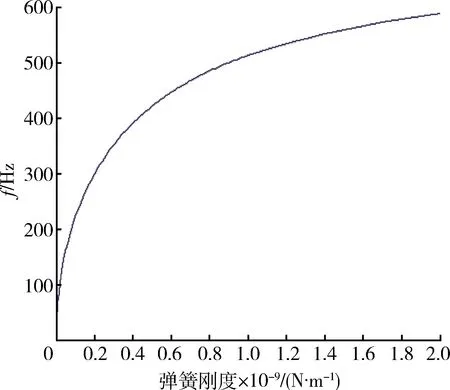
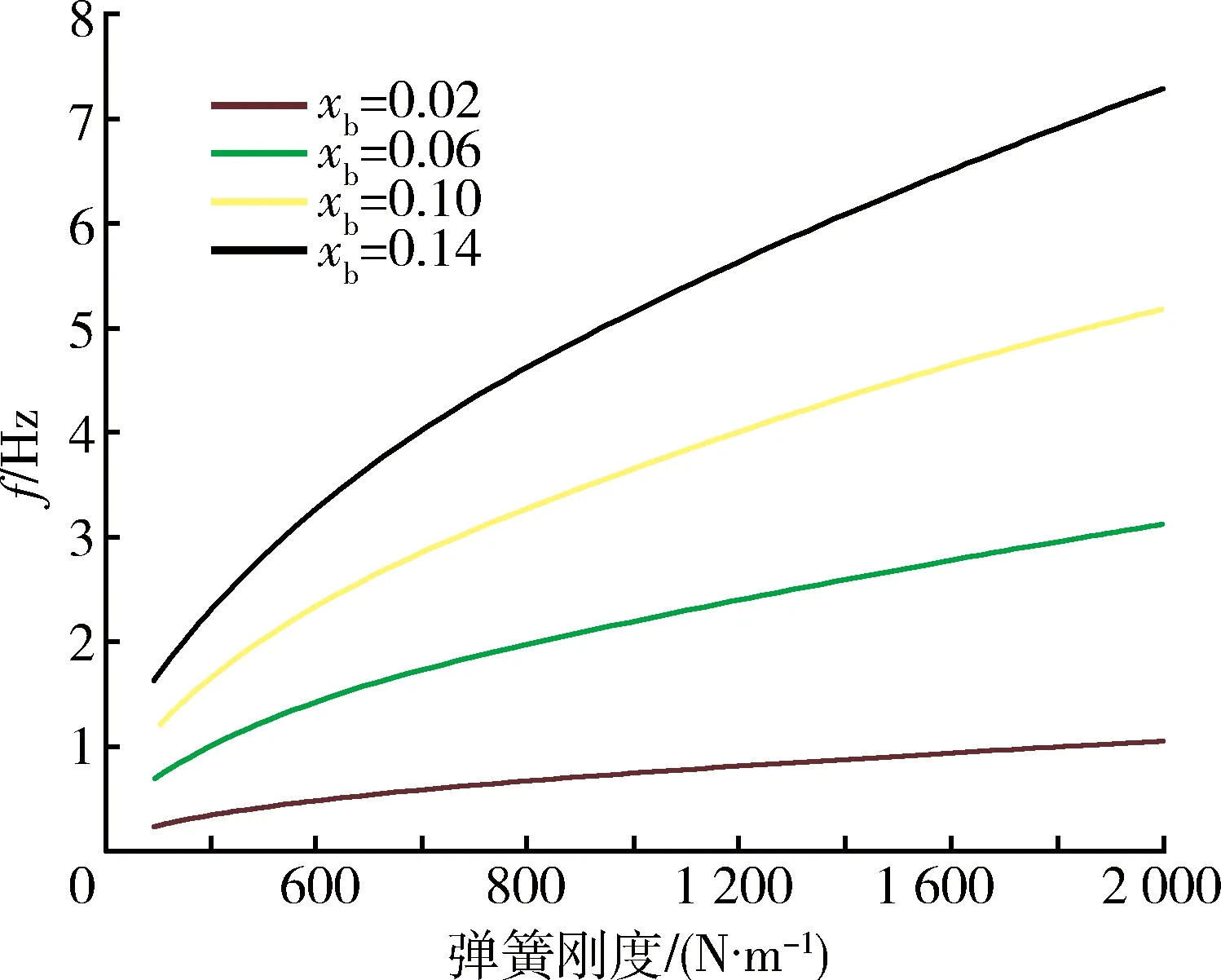
將梁分為2部分進行考慮,xi(i=1,2)表示梁橫截面位置坐標,其中0 梁的彎曲振動微分方程為 (1) 設(shè)a2=EI/ρA,則式(1)變?yōu)?/p> (2) 對式(2)的求解可以采用分離變量法。假定式(2)的解有如下形式 w(x,t)=φ(x)q(t). (3) 將式(3)代入式(2),化簡后得 (4) 此方程兩邊必須等于同一常數(shù),設(shè)此常數(shù)為,可得 (5) 設(shè)式(5)的基本解為φ(x)=esx,則特征方程為 s4-β4=0. (6) 其特征根為±iβ和±β,則其上述特征方程通解為 φ(x)=Asinβx+Bcosβx+Csinhβx+Dcoshβ, (7) 式中:積分常數(shù)A,B,C,D由邊界條件確定,其典型邊界條件見表1。 表1 梁橫向振動典型的邊界條件Table 1 Typical boundary conditions of bending vibration beams 由上述邊界條件以及彈性支承處連續(xù)性方程可得 M處:ω1(0)=0,M1(0)=0; N處:M2(1-xb)=0,Q2(1-xb)=0; B處:ω1(xb)=ω2(0),θ1(xb)=θ2(0); M1(xb)=M2(0),Q1(xb)-Q2(0)=kω2(0). 將振型函數(shù)代入邊界條件,可得 (8) 上述式(8)方程組有非零解的條件為 (-2(k/B)sin(βxb)sinh(βxb)cos(β(l-xb))· cosh(β(l-xb))-(k/B)sin(βxb)·sinh(βxb)·cosh(β(l-xb))cosh(β·(l-xb))-(k/B)sin(βxb)· sinh(βxb)cos(β(l-xb))cos(β(l-xb))-(k/B)· sin(βxb)sinh(βxb)sin(β(l-xb))sin(β(l-xb))+ (k/B)sin(βxb)sinh(βxb)sinh(β(l-xb))· sinh(β(l-xb))+(k/B)sin(βxb)sin(β(l-xb))· cosh(β(l-xb))cosh(βxb)-(k/B)sin(βxb)· cos(β(l-xb))sinh(β(l-xb))cosh(βxb)-(k/B)· sinh(βxb)sin(β(l-xb))cos(βxb)cosh(β(l-xb))+ (k/B)sinh(βxb)cos(β(l-xb))cos(βxb)· sinh(β(l-xb))+2sin(βxb)sinh(βxb)cosh(β· (l-xb))sin(β(l-xb))+2sin(βxb)sinh(βxb)· sinh(β(l-xb))cos(β(l-xb))+2sin(βxb)cosh(β· (l-xb))cosh(βxb)cos(β(l-xb))+2sin(βxb)· sinh(β(l-xb))cosh(βxb)sin(β(l-xb))+ 2sinh(βxb)sin(β(l-xb))cos(βxb)sinh(β· (l-xb))-2sinh(βxb)cos(β(l-xb))cos(βxb)· cosh(β(l-xb))-2cos(β(l-xb))cos(βxb)· sinh(β(l-xb))cosh(βxb)+2sin(β(l-xb))· cos(βxb)cosh(β(l-xb))cosh(βxb)=0, (9) 式中:B=EIβ3。 根據(jù)式(9)并利用數(shù)值方法[12]求出某些特定狀態(tài)下的β,進而可以進一步求出梁的振動固有頻率ω,并且可以分析不同參數(shù)對振動頻率的影響。 首先驗證上述理論的準確性,采用有限元分析軟件進行建模計算,建立的模型如圖3所示。 圖3 梁的振動頻率有限元計算模型Fig.3 Finite element model of bending vibration beams 其中梁的截面尺寸為0.03 m×0.03 m,長度為0.2 m,材料屬性如下:密度為7 800 kg/m3,彈性模量200 GPa,泊松比為0.3。約束條件為一端簡支,中間彈性支承,支承點位置距端點0.02 m。彈簧取值在106~107N/m范圍內(nèi),理論值和計算值結(jié)果對比如圖4所示。 由圖4中曲線可以看出,理論值和軟件仿真計算值基本一致,上述理論能夠準確得出一端簡支,中間彈性支承的梁的振動頻率。 圖4 有限元計算與理論推導(dǎo)結(jié)果對比Fig.4 Theoretical value and calculated value 3.1 材料有效比剛度對振動頻率的影響 研究材料有效比剛度對頻率的影響,仍然采取上文所建立模型,幾何參數(shù)不變,在彈簧剛度變化范圍為100~2 000 N/m時,改變模型材料屬性,研究梁的頻率的變化情況。材料參數(shù)特性如表2所示。 表2 幾種典型材料參數(shù)Table 2 Typical material parameters 梁的振動頻率和比剛度的關(guān)系如圖5所示。 圖5 不同材料梁的振動頻率Fig.5 Frequency of beams for different materials 從圖5中可以看出,梁的有效比剛度越大,振動頻率越高。同時可以看到,當彈簧剛度較小時,不同材料的梁振動頻率相差不大,說明彈簧剛度對振動的影響起主要作用,有效比剛度影響較小;當彈簧剛度值較大時,有效比剛度對振動頻率影響較大,不同材料的梁振動頻率差距明顯。 3.2 彈簧彈性系數(shù)對振動頻率的影響 固定支承位置,彈簧彈性系數(shù)從10~2×109N/m范圍內(nèi)變化時,梁的振動頻率的變化規(guī)律如圖6所示。 圖6 梁振動頻率隨彈簧剛度變化圖Fig.6 Frequency of beams for different spring stiffness 在彈簧支撐位置和材料參數(shù)保持不變的情況下,梁的固有頻率隨著彈簧剛度的增大而增加,但是彈簧剛度增大到一定值之后,固有頻率的增長趨勢趨于緩和。這說明當彈簧剛度在一定的低范圍內(nèi)(0~2×109N/m)變化時,對頻率影響較大,當大于一定范圍內(nèi)時,對頻率影響明顯減弱。 3.3 彈性支承位置對振動頻率的影響 固定彈簧的彈性系數(shù)等條件,改變彈簧的支承位置,研究不同支承位置下梁的振動頻率的變化。 梁的振動頻率和支承位置的關(guān)系如圖7所示。從圖中可以看出在特定的彈簧剛度范圍內(nèi)(k=100~2 000 N/m)梁的固有頻率隨著支承位置Xb值的增大而增大。支承位置離簡支點較近時,頻率隨彈簧剛度變化不大,支承位置離簡支點越遠,彈簧剛度對頻率的影響越明顯。 圖7 梁振動頻率隨支承位置變化圖Fig.7 Frequency of beams for different support locations 本文推導(dǎo)了彈性支承等截面直梁彎曲振動的頻率方程,從頻率方程中得到在某些特定狀態(tài)下的一階固有頻率,并分析了影響頻率的參數(shù)及變化規(guī)律。支承條件確定的情況下,梁的固有頻率會隨著梁的有效比剛度的增長而增大,另外,固有頻率隨著支承位置xb值的增大呈現(xiàn)增大的趨勢。梁的固有頻率隨著彈簧剛度的增大而增加,但是彈簧剛度增大到一定值之后,固有頻率的增長趨勢趨于緩和。這說明當彈簧剛度在一定的低范圍內(nèi)(0~2×109N/m)變化時,對頻率影響較大,當大于一定范圍內(nèi)時,對頻率影響明顯減弱。 [1] 季文美,方同,陳松漠.機械振動[M].北京:科學(xué)出版社,1985. JI Wen-mei,F(xiàn)ANG Tong,CHEN Song-mo. Mechanical Vibration[M]. Beijing:Science Press,1985. [2] THOMSON W T. Theory of Vibration with Applications[M].New Jersey:Prentice-Hall,Inc,Englewwood Cliffs,1972. [3] 楊曉東,金基鐸,鄒光勝.不同支承條件下彎曲振動梁的頻率方程及特征值[J].沈陽航空工業(yè)學(xué)院學(xué)報,2000,17(4):1-6. YANG Xiao-dong,JIN Ji-duo,ZOU Guang-sheng. Freguency Equations and Eigenvalues of Different Supported Beams[J].Journal of Shenyang Institute of Aeronautical Engineering,2000,17(4):1-6. [4] 宋殿義,蔣志剛,陳北雁.彈性支承梁自振頻率分析[J].江蘇建筑,2005,19(1):30-31. SONG Dian-yi,JIANG Zhi-gang,CHEN Bei-yan. Analysis on Self-Vibration Frequency of Strut Beam[J]. Jiangsu Construction,2005,19(1):30-31. [5] 馬連生,歐志英,黃達文.不同梁理論之間簡支梁特征值的解析關(guān)系[J].工程力學(xué),2006,23(10):91-95. MA Lian-sheng,OU Zhi-ying,HUANG Da-wen. Analytical Relationships of Simply-Supported Beam’s Eigenvalues Using Different BeamTheories[J]. Engineering Machanics,2006,23(10):91-95. [6] CHENG Y K,ZHOU Ding. Vibrations of Rectangular Plates with Elastic Intermediate Line-Supports and Cons Traits[J]. Thin-Walled Structures,2000,37(3):305-331. [7] HUANG M H,THAMBIRATNAM D P . Free Vibration Analysis of Rectangular Plates on Elastic Intermediate Supports[J]. Journal of Sound and Vibration,2001,240(3):567-580. [8] XU Ming-tian,CHENG De-lin. A New Approach to Solving a Type of Vibration Problem[J]. Journal of Sound and Vibration,1994,177(4):565-571. [9] 許明田,程德林.用積分方程法解板的振動問題[J].應(yīng)用數(shù)學(xué)和力學(xué),1996,17(7):655-660. XU Ming-tian,CHENG De-lin. Solving Vibration Problem of Thin Plates Using Integral Equation Method[J]. Applied Mathematics and Mechanics,1996,17(7):655-660. [10] 趙鳳群,王忠民.點彈性支承的非保守矩形薄板的穩(wěn)定性[J].西安理工大學(xué)學(xué)報,1998,14(4):398-403. ZHAO Feng-qun,WANG Zhong-min. The Stability of Non-Conservative Rectangular Plate with Spring Attachments[J]. Journal of Xi’an University of Technology,1998,14(4):398-403. [11] 趙鳳群,王忠民,劉宏昭.轉(zhuǎn)動慣量和彈性支承對非保守桿穩(wěn)定性的影響[J].工程力學(xué),2005,22(4):38-42. ZHAO Feng-qun,WANG Zhong-min,LIU Hong-zhao. Effects of Moment of Inertia and Internal Elastic Supports on the Stability of Non-Conservative Rods[J]. Engineering Machanics,2005,22(4):38-42. [12] 龔純,王正林.MATLAB語言常用算法程序集[M].北京:電子工業(yè)出版社,2008. GONG Chun,WANG Zheng-lin. The Aggregate of MATLAB Algorithm Programming[M]. Beijing: Publishing House of Electronics Industry,2008. [13] 吳云書.材料的比強度和比剛度[J].宇航學(xué)報,1985,7(3):81-85. WU Yun-shu. The Specific Strength and Specific Stiffness of Materials[J]. Journal of Astronautics,1985,7(3):81-85. Influencing Factors of Elastic Supported Beams Frequency MA Chen-guang,LIU Chang-hong,CHEN Xiao-lan (Beijing Institute of Electronic System Engineering, Beijng 100854, China) The frequencies of a typical structure folding rudder are investigated by simplifying the folding rudder into a beam. For beams with internal elastic supports, the vibration equations at each section and continuous conditions at internal elastic supports as well as boundary conditions are given. Based on the bending vibration differential equation and its general solution of the beams, the analytical expressions of frequency equation of bending vibration beams with the elastic support are derived. And the frequencies are calculated by using numerical method. The influences on the frequency by the coefficient of the spring, the specific stiffness and the location of the elastic support are analyzed. elastic support; vibration equation; spring stiffness; specific stiffness; support location 2014-03-10; 2014-07-18 有 馬晨光(1988-),男,河北衡水人。助工,碩士,研究方向為飛行器結(jié)構(gòu)力學(xué)。 通信地址:100854 北京市142信箱30分箱 E-mail:billzhuyan@gmail.com 10.3969/j.issn.1009-086x.2015.03.008 TJ761.1+3;TJ760.3 A 1009-086X(2015)-03-0043-06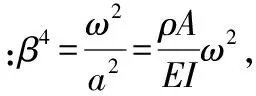

3 計算結(jié)果與分析

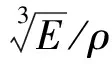
4 結(jié)束語

