防空導彈隨動定向戰斗部自校正控制研究*

滕璽，米雙山，張王衛

(軍械工程學院，河北 石家莊 050003)

防空導彈隨動定向戰斗部自校正控制研究*

滕璽，米雙山，張王衛

(軍械工程學院，河北 石家莊 050003)

建立了防空導彈隨動定向戰斗部模型，提出了運用最小方差控制、廣義最小方差控制分別同帶遺忘因子的遞推最小二乘法配合的自校正控制以及廣義預測控制，對比了這幾種方法的特點、效果與不足，并展望了未來防空導彈隨動定向戰斗部控制策略的發展方向。仿真結果表明，自校正控制在防空導彈隨動定向戰斗部系統中能起到良好的效果，特別在面對非最小相位系統時，廣義預測控制體現了它特有的優勢。

隨動定向戰斗部；自校正控制；最小方差控制；廣義預測控制

0 引言

防空導彈武器系統是國家防空力量的重要組成部分，在國土防空和信息化戰爭中負有重要使命[1]。但是其所需要對付的空中目標的機動性和防御能力越來越強，戰斗機、直升機、無人機以及空襲導彈(air ballistic missile,ABM)這類目標的特點是能夠低空飛行，有一定的機動性和防護性；戰術彈道導彈(tactical ballistic missile,TMB)，這類目標的特點是速度快，機動性差[2]。

防空導彈隨動定向戰斗部[3]就是利用伺服系統，控制戰斗部對準目標實施定向爆破，提高破片和裝藥利用率的戰斗部。這樣可以降低對導彈本身的過載要求，提高毀傷能力。

由于飛行速度和高度的變化以及大過載的產生，使得防空導彈在整個飛行的過程中，彈體各項參數劇烈變化，隨動定向戰斗部控制效果受到嚴重影響[4]。對于現行的隨動定向戰斗部，一般采用閉環回路來減弱參數變化時對系統的影響，但這種方法并不能完全消除這種影響[5]。為進一步提高控制性能，有必要采用自適應控制。自校正控制[6-7]是自適應控制的一種，它適用于結構已知，但參數未知而恒定或參數緩慢變化的系統。采用自校正控制需要辨識被控系統的參數，并自動校正控制作用，達到預期的控制效果。用自校正控制技術設計防空導彈隨動定向戰斗部，能夠使被控系統適應參數變化，保持較好的性能。

1 防空導彈隨動定向戰斗部模型的建立

防空導彈隨動定向戰斗部控制回路的模型如圖1所示。

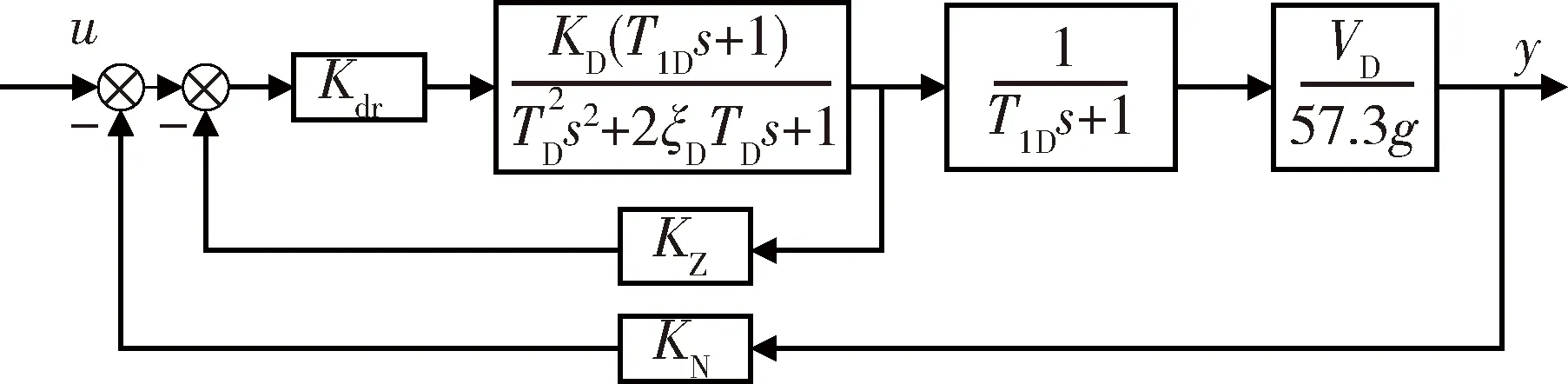
圖1 防空導彈隨動定向戰斗部控制回路Fig.1 Control circuit of servo aimable warhead of anti-aircraft missile

圖中，u為控制輸入，經過舵機、彈體(含阻尼回路)，生成角加速度信號，并經信號變換輸出y為過載，Kdr為控制信號增幅，KZ為位置反饋，KN為加速度反饋。其阻尼回路的傳遞函數為

(1)

式中：

加速度回路傳遞函數為

(2)

式中：

考慮控制系統受到噪聲干擾，被控對象的差分方程為

A(q-1)y(t)=q-dB(q-1)u(t)+C(q-1)ζ(t),

(3)

式中：

A(q-1)=1+a1q-1+…+anqna,

B(q-1)=b0+b1q-1+…+bmq-m,

C(q-1)=c0+c1q-1+…+clq-l.

2 防空導彈隨動定向戰斗部自校正控制方案的確定

自校正控制是目前應用最廣的一類自適應控制方法。它的基本思想是將參數估計遞推算法與各種不同類型的控制算法結合起來，形成一個能自動校正控制器參數的實時控制系統[8]。自校正控制既能完成調節任務，也能進行伺服跟蹤，完成控制任務，它主要應用于結構已知但參數未知而恒定的隨機系統，也適用于結構已知但參數緩慢變化的隨機系統[9]。

根據某導彈彈道參數[10]，可知，防空導彈隨動定向戰斗部的結構已知且參數為慢時變的，所以可以用自校正的方法予以控制。

防空導彈隨動定向戰斗部結構為

a0y(k)+a1y(k-1)+a2y(k-2)=

q-d[b0u(k)+b1u(k-1)]+c0ξ(k)+c1ξ(k-1).

(4)

2.1 最小方差控制

最小方差自校正控制器[11]要求系統的輸出y(t)在噪聲干擾和參數變化的情況下，能很好地跟蹤參考輸入yr(t)。B(z-1)為Hurwitz多項式，即對象是最小相位或逆穩定，則有：

設控制目標是使實際輸出y(k+d)跟蹤期望輸出yr(k+d)，使性能指標

J=E{[y(k+d)-yr(k+d)]2}

(5)

為最小，則最小方差控制律為

F(z-1)u(k)=C(z-1)yr(k+d)-G(z-1)y(k).

(6)

2.2 廣義最小方差控制

在求解控制律的性能指標中引入對控制量的加權項，從而限制控制作用過于劇烈變化；另外，只要適當選擇性能指標中的各加權多項式，廣義最小方差控制可以適用于非最小相位系統。

設被控對象如式(4)，選擇性能指標函數：

J=E{[P(z-1)y(k+d)-R(z-1)·yr(k+d)]2+[Q(z-1)u(k)2]},

(7)

式中:y(k+d)，yr(k+d)分別為第(k+d)時刻的系統實際輸出及期望輸出；u(k)為第k時刻的控制量；P(z-1)，R(z-1)和Q(z-1)分別為實際輸出、期望輸出和控制量的加權多項式，它們分別具有改善閉環系統性能、柔化期望輸出和約束控制量的作用：

P(z-1)=1+p1z-1+p2z-2+···+pnpz-np,

R(z-1)=r0+r1z-1+r2z-2+···+rnrz-nr,

Q(z-1)=q0+q1z-1+q2z-2+···+qnqz-nq.

控制系統的設計目的是選擇控制律，使得式(7)中的性能指標J最小。

對于對象(3)，使性能指標(7)最小的廣義最小方差控制律為

(8)

或

u(k)=[C(z-1)R(z-1)yr(k+d)-

F(z-1)P(z-1)].

(9)

2.3 廣義預測控制

預測控制不是某一種統一理論的產物，而是源于工業實踐，在積極吸收其他學科的思想、方法和成果的基礎上，并在工業實踐過程中發展和完善起來的一類計算機控制算法[12]。各類預測控制算法的共性可概括為3點：預測模型、滾動優化和反饋校正。這三要素也是預測控制區別于其他控制方法的基本特征，同時也是預測控制在實際工程應用中取得成功的技術關鍵。

2.4 隨動定向戰斗部自校正控制方案中的參數辨識

為了實現自校正控制，必須選用一種合適的在線辨識方法來估計對象的參數。可用的在線辨識方法很多，每種方法都各有其特點，當與自校正控制相結合時，就存在適用性問題，就是指辨識精度、收斂速度、運算量、內存占有量及結合自校正控制后的效果等能否滿足工程技術要求。

考慮辨識方法結合對象模型和最小方差自校正進行計算，遞推最小二乘法對時變參數具有較強的跟蹤能力，并具有一定的抗干擾性。這里采用帶遺忘因子的遞推最小二乘法。

取性能指標為

(10)

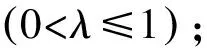
針對式(10)的目標函數，與遞推最小二乘法的推導過程相同，可得遺忘因子遞推最小二乘參數估計的公式：

3 隨動定向戰斗部自校正控制方案的仿真

為了便于仿真研究，假設研究對象(防空導彈隨動定向戰斗部)的數學模型為

y(k)-1.7y(k-1)+0.7(y-2)=

u(k-4)+0.5u(k-5)+ξ(k)+0.2ξ(k-1)，

(12)

式中:ξ(k)為方差為0.1的白噪聲。

3.1 最小方差自校正控制仿真

采用最小方差自校正控制間接算法：

a=[1 -1.7 0.7]; b=[1 0.5]; c=[1 0.2]; d=4; %對象參數

……

u(k)=(-f(2:nf+1)*uk(1:nf)+ce*[yr(k+d:-1:k+d-min(d,nc));yrk(1:nc-d)]-g*[y(k);yk(1:na-1)])/f(1); %求控制量

……

運行結果如圖2所示。

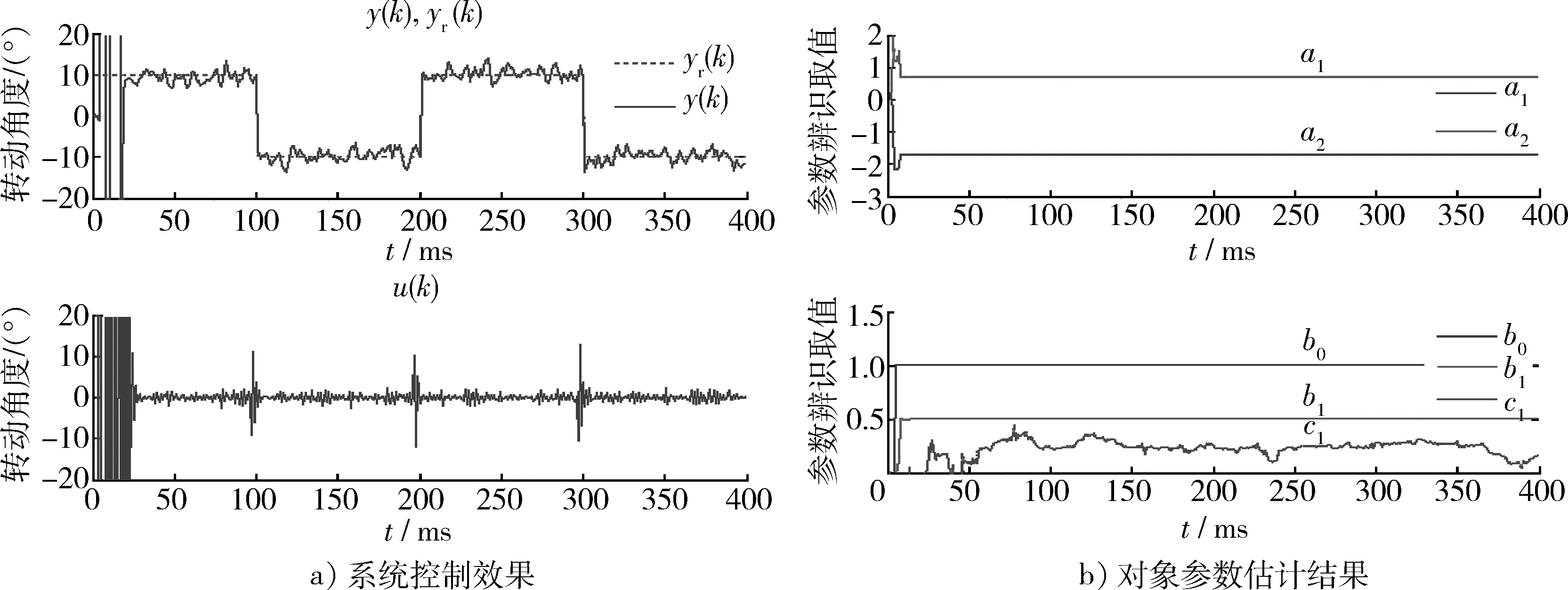
圖2 最小方差控制最小相位系統效果圖Fig.2 MVC rendering minimum phase system

當防空導彈隨動定向戰斗部為最小相位系統時，最小方差自校正控制較為穩定，得到良好的控制效果，被控對象參數估計結果準確。

3.2 廣義最小方差自校正控制仿真

在飛行過程中，防空導彈隨動定向戰斗部不一定為最小相位系統，當被控對象為

y(k)-1.7y(k-1)+0.7(y-2)=u(k-4)+

2u(k-5)+ξ(k)+0.2ξ(k-1),

(13)

即為被控對象不是最小相位系統，控制系統的開環傳遞函數的所有極點和零點沒有都位于s左半平面。

若采用一般的最小方差自校正控制，則會得到如3圖結果，完全達不到控制的效果，體現出了最小方差自校正不能適用于非最小相位系統的缺點。

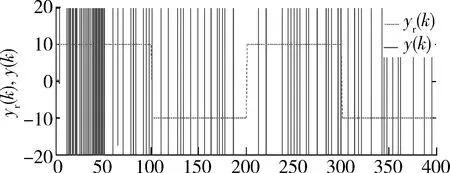
圖3 最小方差控制非最小相位系統效果圖Fig.3 MVC rendering non-minimum phase system

最小方差控制只能用于最小相位系統，即逆穩定系統，且對靠近單位圓的穩定零點非常靈敏，當干擾方差較大時，由于需要一步完成校正，所以控制量的方差也很大，這將加速執行機構的磨損。

對上述非最小相位系統，取加權項P(z-1)=1,R(z-1)=1和Q(z-1)=2，采用廣義最小方差自校正控制如下：

a=[1 -1.7 0.7]; b=[1 2]; c=[1 0.2]; d=4; %對象參數

……

Pw=1; R=1; Q=2; %加權多項式P，R，Q

np=length(Pw)-1; nr=length(R)-1; nq=length(Q)-1;

……

得到結果如圖4所示。

采用廣義最小方差自校正控制，可以通過調整加權項，適用于非最小相位系統，但是控制效果一般，并且加權項的選擇十分不易。

3.3 廣義預測控制仿真

得到結果如圖5所示。

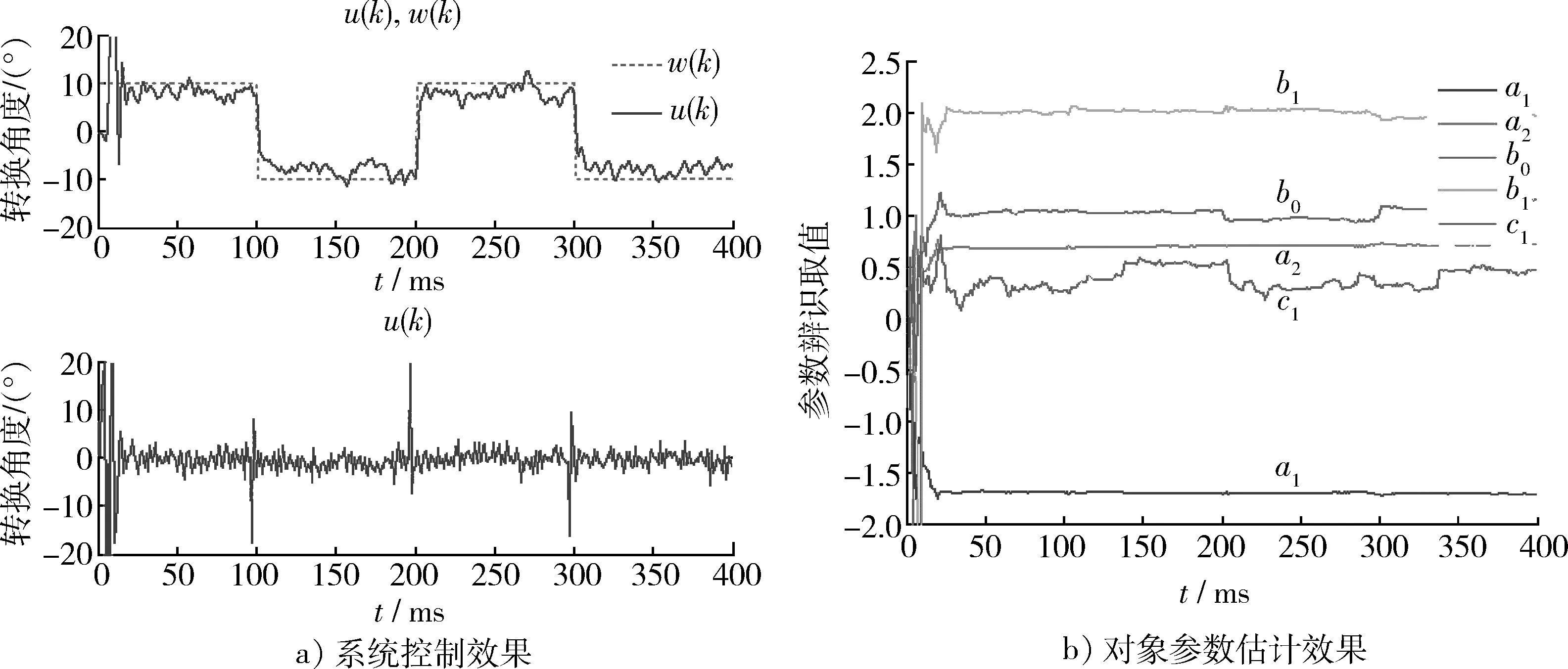
圖4 廣義最小方差控制非最小相位系統效果圖Fig.4 GMVC control rendering minimum phase system

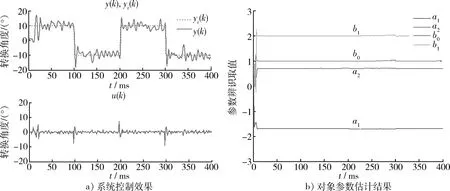
圖5 廣義預測控制效果圖Fig.5 Generalized predictive control effect

與最小方差控制相比，廣義最小方差控制在性能上有很大改善，能夠實現對非最小相位系統的控制，并對控制作用有一定的約束，但在實際工程應用中，如何選擇適當的加權多項式，有比較大的困難。廣義預測控制是一種魯棒性強、能夠有效地克服系統滯后、可應用于開環不穩定非最小相位系統的先進控制算法，解決了廣義最小方差自校正控制關于加權項的選擇不易的問題。但是由于它需要Diophantine方程計算、矩陣求逆和最小二乘的遞推求解，因此計算量比較大。

4 結束語

最小方差控制是自校正控制的基礎，比較穩定地控制防空導彈隨動定向戰斗部，但是當系統為非最小相位系統時，失去了控制能力；廣義最小方差控制解決的最小方差控制的關于不能控制非最小相位系統等問題，但是又帶來了加權項不易選擇的問題；廣義預測控制進一步改進了廣義最小方差控制，解決了加權項選擇問題，但是計算量偏大。

防空導彈隨動定向戰斗部的控制要在穩定的基礎上提高精度，才能保證戰斗部的毀傷效果，加上在防空導彈飛行過程中的各種影響要素很多，抗干擾性也是不能忽視的一點。對于導航來說，在飛行前端，精度的要求不是很高，但是到了飛行后段，精度的要求就越來越明顯了。因此，結合智能方法的自校正控制方法在防空導彈隨動定向戰斗部控制方面有很好的應用前景。

[1] 彭立影，賈希勝，韓永新. 用于評估地空導彈系統效能的模糊綜合模型[J]. 現代防御技術，2012，40(2)：13-16. PENG Li-ying, JIA Xi-sheng, HAN Yong-xin. Ambiguity Comprehensive Valuation Model of System Effect on the Surface to Air Missile [J]. Modern Defence Technology, 2012, 40(2): 13-16.

[2] 鐘凌偉. 伴隨法在防空導彈脫靶量研究中的應用[J]. 現代防御技術，2012，40(6):46-50. ZHONG Ling-wei. Application of Adjoint Method in the Study of Miss Distance of Air Defense Missile [J]. Modern Defence Technology, 2012, 40(6): 46-50.

[3] TALLY JAMES C, Dahlgren Va. Aimable Warhead: USP, 5182418[P]. 1993.

[4] RICHARD M L. Physics of Direct Hit and Near Miss Warhead Technology [M]. Alexander Bell Driver, Reston, Virginia: American Institute of Aeronautics and Astronautics, Inc, 2001: 4-8.

[5] 郝福建，于云峰，仝浩，等. 戰術導彈自動駕駛儀變結構控制設計與仿真[J]. 計算機仿真，2009，26(7)：90-94. HAO Fu-jian, YU Yun-feng, TONG Hao, et al. Design and Simulation of Tactical Missile’s Autopilot Based on Variable Structure Control [J]. Computer Simulation, 2009, 26(7): 90-94.

[6] 徐湘元. 自適應控制理論與應用[M]. 北京：電子工業出版社，2007. XU Xiang-yuan. Adaptive Control and application [M]. Beijing: Electronic Industry Press, 2007.

[7] 師黎，陳鐵軍，李曉媛，等. 智能控制理論及應用[M]. 北京：清華大學出版社，2009. SHI Li, CHEN Tie-jun, LI Xiao-yuan, et al. Intelligent Control Theory and Applications [M]. Beijing: Tsinghua University Press, 2009.

[8] 龐中華，崔紅. 系統辨識與自適應控制MATLAB仿真[M]. 北京：北京航空航天大學出版社，2009. PANG Zhong-hua, CUI Hong. System Identification and Adaptive Control MATLAB Simulation [M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2009.

[9] ASTROM K J, BORISSON U, LJUNG L, et al. Theory and Applications of Self-Tuning Regulators[J]. Automatica，1997，13(5)：456-476.

[10] 陳堯，張靖，王帥. 小型戰術導彈捷聯慣導算法及仿真平臺研究[J]. 彈箭與制導學報，2010，30(1)：33-36. CHEN Yao, ZHANG Jing, WANG Shuai. Research on Strapdown Algorithm and Simulation Workbench Based on Small Tactical Missile [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(1): 33-36.

[11] BERSINI H，VARELA F. Hints for Adaptive Problem Solving Gleaned From Immune Network[C]∥ Parall Problem Solving from Immune Nature，Berlin Heidelberg：Springer-Verlag，1991：343-354.

[12] 時維國，邵誠，孫正陽. 基于AR模型時間延預測的改進GPC網絡控制算法[J]. 控制與決策，2012，27(3)：477-480. SHI Wei-guo, SHAO Cheng, SUN Zheng-yang. Improved GPC Network-Control Algorithm Based on AR Model Time-Delay Prediction [J]. Control and Decision, 2012, 27(3): 477-480.

Self-Tuning Control of Servo Aimable Warhead of Antiaircraft Missile

TENG Xi, MI Shuang-shan, ZHANG Wang-wei

(Ordinance Engineering College, Hebei Shijiazhuang 050003, China)

The model of the servo aimable warhead of antiaircraft missile is established. Then, the methods that the minimum variance control (MVC) and generalized minimum variance control (GMVC) with forgetting factor and generalized predictive control (GPC) are proposed. The characteristics, effect and disadvantage of these methods are compared, and the development direction of servo aimable warhead of antiaircraft missile is prospected. The simulation results show that self-tuning control can play good effect and GPC embodies especially the unique advantages in non-minimum-phase system.

servo aimable warhead; self-tuning control; minimum variance control(MVC); generalized predictive control(GPC)

2013-12-25；

2014-07-05

滕璽(1989-)，男，四川內江人。碩士生，主要從事系統建模與仿真方面的研究。

通信地址：233000 安徽省蚌埠市裝甲兵學院教練團汽車一連 E-mail：jxxytxttx@126.com

10.3969/j.issn.1009-086x.2015.03.009

TJ760.3;TP273

A

1009-086X(2015)-03-0049-06