帶有高階滑模微分器的制導控制一體化設計*

周覲，雷虎民，李炯，邵雷

(空軍工程大學 防空反導學院，陜西 西安 710051)

帶有高階滑模微分器的制導控制一體化設計*

周覲，雷虎民，李炯，邵雷

(空軍工程大學 防空反導學院，陜西 西安 710051)

針對制導控制一體化模型中由于目標機動加速度難以測量的問題，提出了應用高階滑模微分器，對導彈導引頭獲得的彈目相對運動信息進行微分，從而解算出目標加速度的方法。在最后開展了導彈六自由度仿真驗證，將高階滑模微分器得到的目標加速度與真實值進行對比，驗證了方法的有效性。

制導控制一體化;高階滑模微分器;滑模控制;反演控制

0 引言

高超聲速飛行器技術的蓬勃發展對我國防空反導體系構成了巨大挑戰，傳統的防空導彈制導與控制性能已經難以抵抗現代戰爭中高超聲速飛行器所帶來的威脅，正因如此，制導控制一體化技術應運而生。與傳統的制導與控制系統分開設計不同，制導控制一體化技術將導彈制導回路與控制回路整合為一個回路，即根據導彈目標的相對運動關系直接得到控制指令，省去了中間的指令過載與控制指令之間的轉換環節，從而能夠有效提高武器制導控制精度，減小脫靶量[1～5]。

Tal Shima等[4]以基于零控零化脫靶量思想建立了導彈俯仰平面制導控制一體化模型，應用滑模控制方法對模型進行了控制，仿真結果表明制導控制一體化設計相比于傳統分回路設計能夠取得更高的制導精度。段廣仁等[5]以零化視線角速率為目標，利用非線性狀態變換將導彈俯仰通道制導控制一體化模型轉換為標準形式，基于滑模思想設計了滑模控制算法。仿真結果表明，在目標機動情況下，該模型相對于傳統分回路設計能夠取得更小的脫靶量。侯明哲等[6]在文獻[5]的基礎上建立了具有嚴格反饋形式的導彈目標三維相對運動狀態模型，應用滑模反演控制方法設計了制導控制一體化算法。六自由度仿真結果表明，在加入目標機動以及導彈自身的不確定性條件下，所設計算法能夠獲得更好的制導精度以及更小的控制能量。Alexander[7]等針對目標信息難以獲得的情況，在制導控制一體化算法中加入了高階滑模微分器對目標狀態進行估計，并通過仿真將改進后制導控制一體化算法與傳統制導控制分開設計算法進行對比，驗證了所設計方法的有效性。董飛垚等[8]應用最優滑模控制理論設計導彈制導控制一體化算法，張保群等[9]設計了導彈俯仰通道制導控制一體化模型，應用滑模自適應反演控制方法對模型進行了控制，仿真結果表明在目標機動和導彈參數攝動情況下，制導控制一體化模型能夠取得更好的制導效果。

對于由于目標機動引起的不確定性以及制導控制所需的目標信息無法有效獲得的問題，現有文獻中大多采用設定不確定性上界的方法，但是對于不同的目標，其不確定性上界會有很大差異，如何有效設定以及估計不確定性的問題不能夠很好解決。本文以此為出發點，應用高階滑模微分器對目標的加速度信息進行估計，從而改進制導控制一體化算法，提高武器性能指標。

1 制導控制一體化模型建立

根據文獻[6]，在三維空間中的導彈和目標相對運動關系可以表示為

(1)

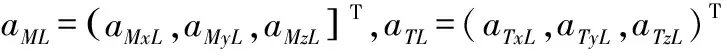
(2)

導彈自動駕駛儀的狀態方程可以表示為[9]

(3)

式中：x1=(γ，β，α)T；x2=(ωx，ωy，ωz)T；u=(δx，δy，δz)T；

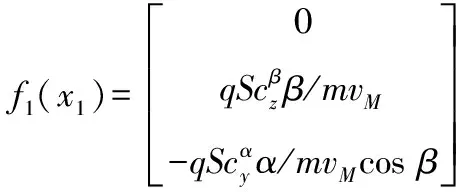
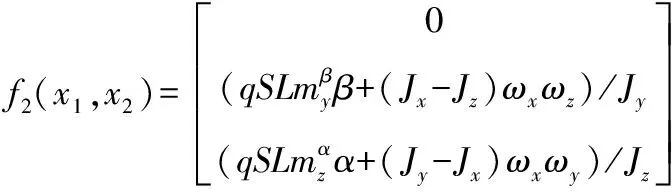
式中：α,β,γ，?分別為導彈攻角，側滑角，滾轉角和俯仰角；q為動壓；S為參考面積；vM為導彈速度。

導彈的加速度分量可以表示為[10]

(4)

(5)

式中：

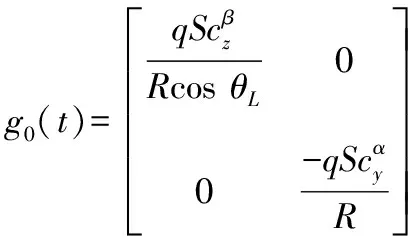
將式(3)和(5)合并，可以得到三維空間的導彈制導控制一體化模型：

(6)

2 高階滑模微分器

從式(6)中可以看出，制導控制一體化算法的求取需要知道目標信息，即目標加速度在視線坐標系下沿Oy軸與Oz軸的分量。傳統的方法是給定目標加速度的上界，應用滑模控制理論求解控制算法，但是對于不同的目標，其加速度上界的確定具有很大不同，而且應用在線估計逼近的方法對于算法的快速性又提出了更高的要求。對此，本文提出應用高階滑模微分器的方法，利用導引頭獲取的彈目相對運動信息，對目標加速度進行準確有效的估計。

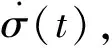
(7)

式中：第2項以及第3項稱為非線性動態滑模面[10]。

SMD的Simulink模塊圖如圖1所示。

待定參數ρ0,a,b需要滿足以下條件：

(8)

定理1[11]：式(7)能夠保證J0在有限時間內收斂到0，并且收斂誤差一階微分為

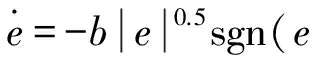
本文認為導彈裝備了主動導引頭，可以測量解算出導彈和目標之間沿視線各個軸向的加速度信息，以及視線仰角θL和視線偏角ψL。導彈和目標之間的相對速度可以表示為

(9)

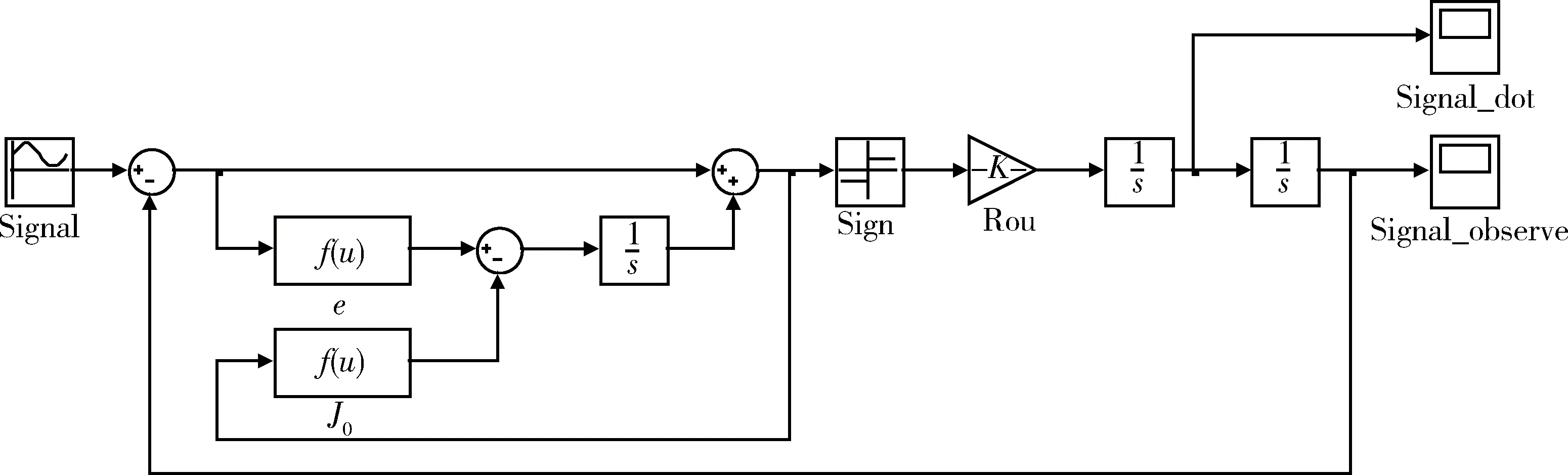
圖1 SMD結構圖Fig.1 Simulink structure of SMD

式中：vT,vM分別為目標和導彈的速度；vrx,vry,vrz分別為視線Ox,Oy,Oz軸的相對速度；DCMTL，DCMML分別表示從目標速度坐標系到視線坐標系以及從導彈速度坐標系到視線坐標系之間的轉換矩陣。將式(9)展開可以得到：

(10)

式中：θT,ψT為目標彈道仰角以及彈道偏角；vTxL，vTyL和vTzL分別為目標速度在視線坐標系下的分量。在末制導階段，導彈和目標進入碰撞三角，認為導彈對準良好，針對迎擊情況即有

cos(ψT-ψL)≈cos(-π)=-1，

則式(10)可以化簡為

(11)

將式(11)進行微分可以得到：

(12)

則目標的加速度信息可以表示為

(13)

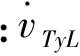
3 制導控制一體化算法設計

定義S0=x0-x0d,其中x0d為狀態變量的目標值，在本文中x0d=0，對S0進行微分可以得到：

(14)

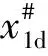
(15)

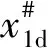
(16)

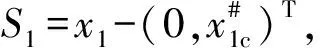
(17)

虛擬控制量可以選為

(18)

式中：k1為待設計參數。同樣使x2d通過一個時間常數為τ2的低通濾波器。

(19)

最后定義S2=x2-x2c，對S2進行微分得到：

(20)

可以得到最后控制量為

(21)

式中：k2為待設計參數。

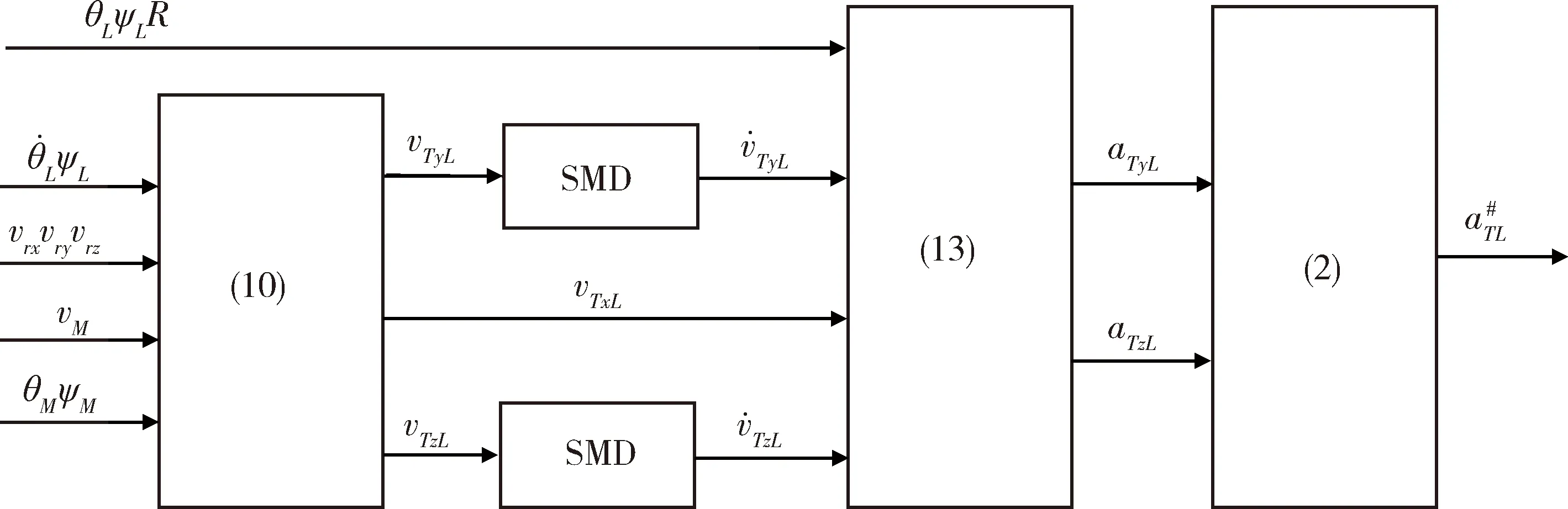
圖2 SMD解算目標加速度Fig.2 Target maneuver estimation block

4 六自由度仿真驗證

為了證明本文所提出的制導控制一體化算法的有效性，開展了導彈六自由度仿真驗證，并且認為導彈滾轉通道穩定不需要控制。

仿真過程中設計的目標的最大過載為15，有關導彈和目標初始狀態參數以及初始彈目視線信息如表1所示。

仿真效果如圖3～7所示。

表1 彈目初始參數及視線信息Table 1 Parameters of the missile, target and line-of-sight (LOS) initial condition

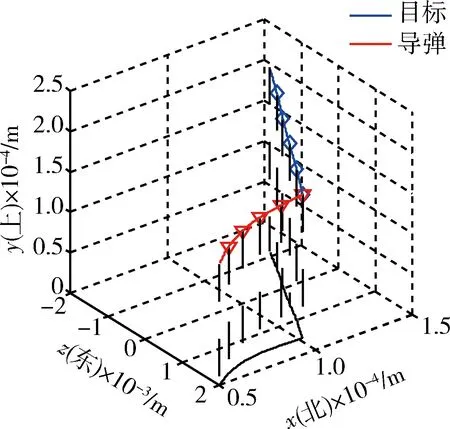
圖3 彈目三維運動軌跡Fig.3 Trajectory of missile and target in three dimensional space

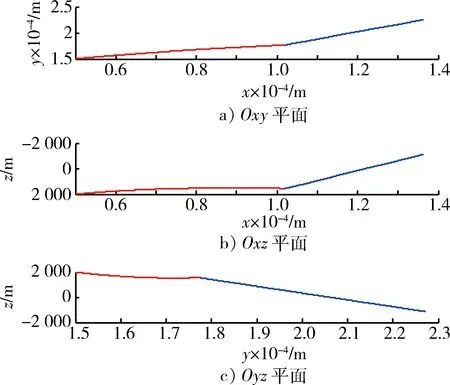
圖4 彈目位置在分平面的投影Fig.4 Trajectory projection to the x, y and z axis

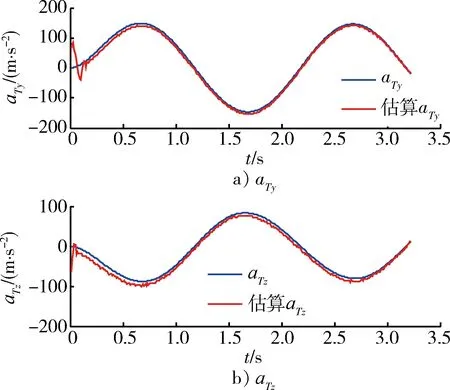
圖5 SMD解算得到目標加速度與真實信息對比圖Fig.5 Comparison of estimated target maneuver with its true information

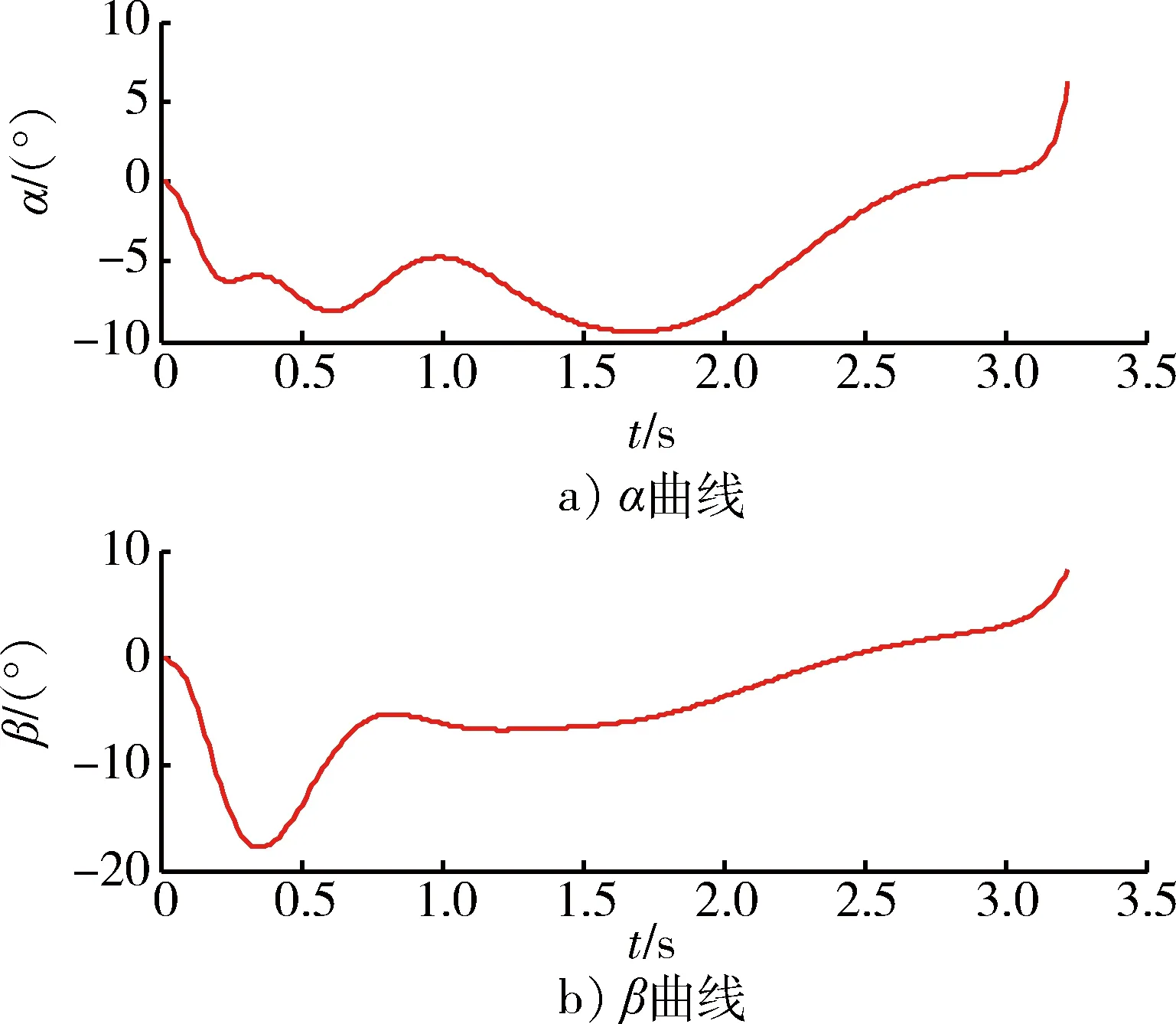
圖6 導彈攻角α和側滑角β變化曲線Fig.6 Curves of α and β

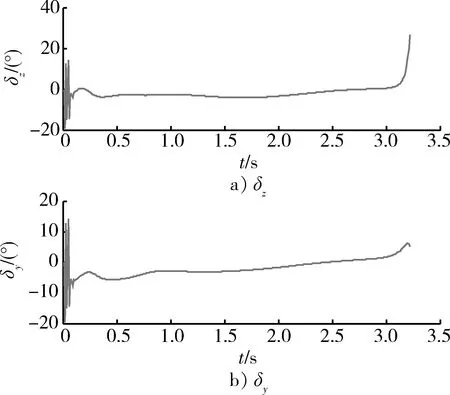
圖7 導彈舵偏角δz和δy變化曲線Fig.7 Curves of fin deflection δz and δy

從圖3和圖4中可以看出，導彈軌跡平穩，最后準確命中目標，其脫靶量為0.463 94 m，達到了碰撞殺傷效果，有力提高了武器制導控制精度。從圖5中可以看到，應用滑模微分器解算得到的目標加速度與目標真實加速度總體上吻合良好，經過大約0.1 s的調節時間后，SMD解算輸出的目標加速度與真實值非常接近，并且在之后的時間內能夠很好的跟蹤目標加速度，驗證了應用SMD對目標加速度進行估計的有效性和準確性。從圖6和圖7中可以看出，導彈姿態變化并不十分劇烈，舵偏角變化比較平穩，除了在開始大約0.1 s范圍內有些抖震現象，這是由于在設定初始條件時導彈導引頭視線角與真實視線角之間設定了5°的初始對準誤差以及此時高階滑模微分器的輸出不穩定，可以看出算法能夠快速消除誤差角，而且在以后的變化過程中比較緩慢，有效驗證了控制算法的快速性和魯棒性。

5 結束語

本文針對制導控制一體化模型算法中目標機動信息難以獲得的問題，引入了高階滑模微分器，通過對導引頭獲得的彈目相對運動信息進行微分，解算出所需的目標加速度信息，從而對算法本身進行了完善提高，提升武器系統的制導控制精度，所研究方法具有一定的理論價值和工程參考價值。

[1] LIN C F, EVER J H. A LTV Dynamics Model for Missile Guidance and Control in the Endgame[C]∥AIAA

Guidance, Navigation, and Control Conference, Washington,1992:1024-1029.

[2] MENON P K, OHLMEYER E J. Integrated Design of Agile Missile Guidance and Autopilot Systems[J]. Control Engineering Practice,2001, 9(10):1095-1106.

[3] XIN M, BALAKRISHNAN S N, OHLMEYER E J. Integreted Guidance and Control of Missiles withθ-D Method[J]. IEEE Transactions on Control Systems Technology，2006, 14(6)：981-982.

[4] SHIMAL T, IDAN M, GOLAN O M. Sliding-Mode Control for Integrated Missile Autopilot Guidance[J]. Journal of Guidance Control and Dynamics，2006, 29(2)：250-260.

[5] 段廣仁,侯明哲,譚峰.基于滑模方法的自適應一體化導引與控制律設計[J].兵工學報,2010,31(2),191-198. DUAN Guang-ren, HOU Ming-zhe, TAN Feng. Adaptive, Integrated Guidance and Control Law Design Using Sliding mode Approach [J]. Acta Armamentar, 2010, 31(2)：191-198.

[6] HOU M Z, LIANG X L, DUAN G R, Adaptive Block Dynamic Surface Control for Integrated Missile Guidance and Autopilot[J]. Chinese Journal of Aeronautics，2013, 26(3):741-750.

[7] Alex Zhurbal, Moshe Idan. Effect of Estimation on the Performance of an Integrated Missile Guidance and Control System[J]. IEEE Transaction on Aerospace and Electronic Systems, 2011, 47(4):2690-2708.

[8] 董飛垚，雷虎民，李海寧，等. 一類帶有加速度約束的非線性系統最優滑模控制[J].控制理論與應用,2012,29(10)：1223-1226. DONG Fei-yao, LEI Hu-min, LI Hai-ning, et al. Optinal Sliding-Mode Control for Nonlinear Systems Subject to Acceleration Constraint[J].Control Theory and Application,2012,29(10):1223-1226.

[9] 張保群,宋申民. 基于自適應滑模控制的導彈制導與控制一體化反演設計[J]. 彈箭與制導學報,2009,29(5):31-35. ZHANG Bao-qun, SONG Shen-min. Integrated Playback Design of Missile Guidance and Control Based on Adaptive Sliding-Mode Control[J]. Journal of Projectiles , Rockets , Missiles and Guidance, 2009,29(5):31-35.

[10] Alex Zhurbal, Moshe Idan. Effect of Estimation on the Performance of an Integrated Missile Guidance and Control System[J]. IEEE Transaction on Aerospace and Electronic Systems, 2011, 47(4):2690-2708.

[11] KRUPP D R, SHKOLNIKOV I A,SHTESSEL Y B. 2-Sliding Mode Control for Nonlinear Plants with Parametric and Dynamic Uncertainties[C]∥AIAA Guidance, Navigation, and Control Conference and Exhibit,Denver, 2000:14-17.

[12] 焦曉紅,關新民.非線性系統分析與設計[M],北京:電子工業出版社,2008. JIAO Xiao-hong, GUAN Xin-min.Analysys and Design of Nonlinear Systems[M].Beijing: Publishing House of Electronic Industry,2008.

Integrated Guidance and Control Design with Sliding Mode Differentiator

ZHOU Jin，LEI Hu-min，LI Jiong，SHAO Lei

(AFEU，Air and Missile Defense School, Shaanxi Xi’an 710051, China)

As the target information in the integrated guidance and control model are difficult to measure, a novel high order sliding mode differentiator (SMD) is introduced to get access to the target acceleration by differentiating the target and missile relative motion information obtained from the missile active homing seeker. The six degree of freedom simulation is carried out and a comparison between the estimated target maneuver information and its true data is made, which successfully verifies the effectiveness the proposed algorithm.

integrated guidance and control; high order sliding mode differentiator; sliding mode control; back-stepping control

2014-05-06；

2014-07-04

航空科學基金項目(20130196004)

周覲(1989-)，男，河北衡水人。碩士生，研究方向為導航制導與控制。

通信地址：710051 陜西省西安市空軍工程大學防空反導學院研2隊 E-mail：zhoujindr@yahoo.com

10.3969/j.issn.1009-086x.2015.03.0014

TJ765

A

1009-086X(2015)-03-0077-06