過程重于結果,思維精益求精
——一道導數綜合題的課堂思維導引
☉江蘇省如東縣掘港高級中學 錢雨森
過程重于結果,思維精益求精
——一道導數綜合題的課堂思維導引
☉江蘇省如東縣掘港高級中學 錢雨森
導數與函數綜合問題,在歷年各省市的高考命題中常以把關題或壓軸題的形式出現,對同學們分析問題與解決問題的能力提出了較高的要求.同樣一道題目,面對不同的解題對象,有的解法繁,有的解法簡,有的草紙遍地,有的一望而答,有的順利求解,有的半途而廢.可見問題的分析過程至關重要.本文以一道導數綜合題為例,談談數學思維過程的優化.
一、問題引出
導數法是研究函數性質問題的有力工具,導數的引入使函數的單調性、最值、極值、零點等問題的解答實現了程序化的處理.前面我們已經學習了利用導數法求含參函數的單調區間,那么反過來,如果已知含參函數在某區間上單調,讓我們求參數的范圍,應如何處理?
題目已知函數f(x)=(2ax-x2)eax,其中a為常數,且a≥0.
(1)略;
本題綜合性強,思維含量高,對同學們的數學基本功提出了更高的要求,要完整順利地解答本題,不僅需要我們具有鍥而不舍的精神和頑強的毅力,還需要具有較強的運算推理能力和探索創造精神.請同學們思考后,給出解答方法.
二、問題探究
思考幾分鐘后,教師請有思路的同學回答.
生1:我們也可以先求單調區間,再將所給的范圍置于相應單調區間內,通過解不等式求解參數的范圍.
師:思維直接,銜接前后,具體如何操作?
生1:求導得f′(x)=[-ax2+(2a2-2)x+2a]eax,令f′(x)= 0,即-ax2+(2a2-2)x+2a=0,利用求根公式得……
師:將問題轉化為無理不等式求解,思路可行,但實際操作過程中難度較高.能否轉變一下思維?
生2:利用導函數在某區間上的正負符號,可得函數在該區間上的增減性,反之,若已知函數在某區間上的增減性,也可得到導函數在該區間的正負,將問題轉化為該區間內不等式恒成立問題求解.
師:思維更上一層樓,但導函數的零點不易求,不等式如何解?
生3:不一定直接求零點,前面我們學習過二次函數零點分布問題,結合二次函數的對稱軸,討論所給區間與零點的關系.
師:非常好,將陌生問題轉化我們所熟悉的問題求解.繼續.
生3:當a=0時,f′(x)=-2x,顯然f′(x)≤0對任意x∈恒成立.
當a>0時,易知判別式Δ=(2a2-2)2+8a2>0恒成立,故二次函數g(x)=ax2-(2a2-2)x-2a有兩個零點.
師:至此問題得到解決,我們再審視一下,在問題的求解中仍需要求解無理不等式,對此能否進一步優化?
生4:可通過討論對稱軸的正負,來避免解答無理不等式.
當a>0時,令h(x)=ax2-(2a2-2)x-2a,則函數h(x)的圖像的對稱軸為直線
師:還有沒有其他解法?
貓眼女人看著他。她用指頭沾點地上的血,舉到鼻子上聞了聞。她明白了什么。她說那你等著吧,我叫人送錢來!貓眼女人打個電話,一輛黑色的奔馳商務車開過來,嘎地一聲在他跟前停下。車上下來幾個穿黑衣黑褲手里拎鋼管的大漢,揪著大福的脖領子問那疼。大福手指指腰,鋼管就砸到腰上;大福手指指腿,鋼管就砸到腿上。直砸得他渾身青腫,跪在地上求饒才罷手。
生5:對于不等式恒成立問題,如果能實現參數分離,可考慮用分離參數法求解!可是不等式ax2-(2a2-2)x-2a≥0中的a卻不能分離出來.
師:當參數不能單獨分離時,應如何考慮?
生6:可考慮參數整體分離.
當a>0時,f′(x)≤0等價于ax2-(2a2-2)x-2a≥0.
師:本題的解答需要同學們具備頑強的品質,并保持思路清晰,目標明確,及時變通,方法得當,才能順利得解.成功地解答一道題目,我們不應滿足于此,而應對相關的問題進行多角度變式探究,這樣既可以鍛煉我們的解題思維,又能培養解題能力.
變式1:已知函數f(x)=x3+ax2+x+1,a∈R.
(1)略;
生7:題意等價于導函數f′(x)=3x2+2ax+1≤0對任意恒成立,即二次方程f(′x)=0的兩根中,一根小于或等于,一根大于或等于
變式2:設函數f(x)=x3+ax2+x+1,a∈R.
(1)略;
生8:f′(x)=3x2+2ax+1,將問題轉化為f′(x)在區間)內有零點.
則問題轉化為如下四種形式.
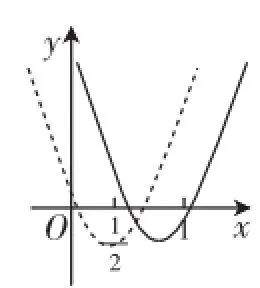
圖1
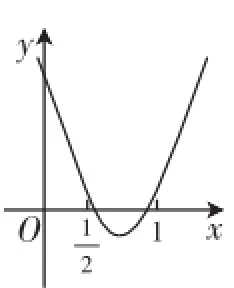
圖2

圖3
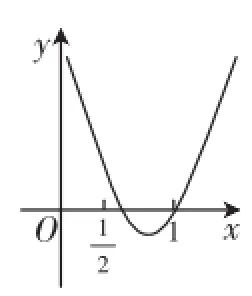
圖4
列出不等式組求解:
生9:利用命題的否定,求參數的范圍,再運用補集思想求出答案.
綜上,每種方法的適用性可能有所局限,在不同特征的題型中應選取不同的方法,各種方法又不是相互獨立的,往往需互相結合使用,切不可被所謂方法局限思維,這也是學習數學的大忌.因此,平時的教學和復習中,要進一步加強思想方法的教學,培養學生的數學意識,提高學生分析問題、解決問題的能力,加強推理探索的教學,培養學生勇往直前的頑強品質,提高學生思維的靈活性和創造性.A

