讓“化歸”成為高中數學解題中的“利器”
☉江蘇省蘇州市第四中學校 薛宏偉
讓“化歸”成為高中數學解題中的“利器”
☉江蘇省蘇州市第四中學校 薛宏偉
解題教學是高中數學課程教學的重要組成部分,學生解題能力的提升一直是數學教師關注的熱點話題;筆者從事高中數學教育教學多年來,一直關注學生解題能力提升的探究,在自身的實踐中深深體會到:化歸數學思想方法的合理運用能夠將高中數學問題“化繁為簡、化難為易、化生為熟……”,進而培養學生在數學解題中的轉化分析能力;在本文中,筆者以理論探究與案例分析相結合的方式進行思考,側重于闡述數學教師從多角度引導學生運用發展和運動的觀點探尋有效的化歸途徑,從而推動學生數學解題效率與質量的快速提升.
一、數形結合,相得益彰,化抽象為形象
數形結合是重要的數學思想方法之一,數形結合與轉化是為了發揮形的生動性和直觀性,發揮數的思路的規范性與嚴密性,兩者相輔相成,揚長避短;實踐證明,數與形的相互轉化與滲透能夠將復雜問題簡單化,抽象的問題具體化、形象化,為解題帶來方便、快捷.
時,使得不等式logx>sin2x(a>0, a≠1)恒成立,試求實數a的取值范圍.
分析:本題若按常規的代數方法進行處理顯得比較抽象、難懂,對于學生而言,求解十分困難,感覺束手無策,但是運用數形結合的思想進行處理,顯得方便、可行;具體解析如下:
構建函數y1=logax和y2=sin2x,根據題意作出圖像,如圖1所示,當a>1時,顯然不成立(舍去),當0<a<1時,只要滿足:當時,能夠使得logax>sin2x恒成立,則可得不等式方程組

圖1
思考:從本題的分析中可以看出:看似復雜的問題在圖形的輔助下變得簡單明了;可見,數形結合的處理手段在數學解題中能夠化抽象為形象,促進了學生思維能力的提升,增強了化歸的靈活性和實效性.
二、緊扣課本,回歸定義,化隱為顯
新課改以來,高中數學考查形式與手段發生了較大的變化,我們經常遇到一些比較特殊的題目,表面看來感覺缺少什么條件似的,給不少學生在解題中帶來了麻煩;但是如果將題設中涉及的數學知識與課本教材聯系起來,歸溯到數學的基本概念與定義,有時候反而能夠挖掘出題設中的隱含信息進行等價轉化,將解題的最佳條件化隱為顯,從而達到“迎刃而解”的目的.
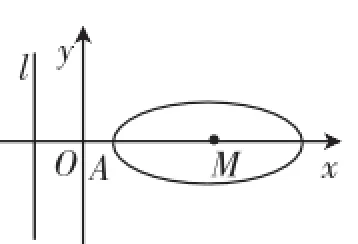
圖2
分析:根據課本教學中拋物線的定義可以知道橢圓上4個點所滿足的條件符合拋物線的性質,結合題意便能揭示出重要的條件“這4個點在拋物線y2=2px上”,這時本題就可以轉化歸結成:p取何值時,拋物線y2=2px與橢存在4個不同的交點.聯立方程可此方程存在兩個不等的正根即可滿足題設條件,則
思考:課本教材中的數學概念往往是處理數學問題基石,從本案例中可以看出處理數學復雜問題時,回歸課本定義能夠靈活挖掘命題中的隱含信息,拓展數學解題的思路,有助于學生分析推理能力的提升,讓學生深刻體會到化歸思想在實際問題中的高效性.
三、空間轉換,圖形演變,化空間為平面
立體幾何一直是高中學生感覺難以理解的問題,主要是需要學生具備一定的空間想象思維能力,在處理空間圖形問題的時候通常是轉化為平面圖形進行處理,異面直線夾角問題、多面體和旋轉體側面上的相關問題,運用這一方式進行處理效果較佳.

圖3

圖4
分析:對于學生而言,空間曲線長度的計算比較困難,沒有任何直接套用的公式和定理的運用,這里如果將圓錐的側面展開成扇形(如圖4所示),這樣空間問題就等價轉化為平面問題;根據幾何關系可得圓錐側邊長PM0=6R,扇形圓心角顯然繩子被分割成一段一段的,當M0M1′、M1M2′、M2M3′……垂直于PN時,繩子的總長最短;由于△PM0N為等邊三角形,則M1′、M2′、M3′……分別是PN、PM1′、PM2′……的中點;這樣繩子的總長度即為以的無窮等比數列各項之和,這時將幾何問題轉化為代數問題進行處理,則繩子總長
思考:在涉及立體幾何的空間問題中,化歸思想的運用比較常見,通過圖形的合理變換,化空間為平面,有效建立立體幾何與平面幾何之間、幾何與代數之間的內在聯系關系,學生探究問題的思路被進一步拓展,培養了學生化歸的敏捷性.
四、動靜結合,相輔相成,化特殊為一般
運動是永恒的,靜止是相對的,辯證唯物主義告訴我們:“事物是在運動變化中不斷發展的”,在探究數學問題過程中,靈活運用運動變化的觀點去看待數學對象時,能夠容易發現這些對象在運動過程中保持不變性的方面;事物發展的普遍規律往往寄寓于特例之中,我們在處理數學問題的時候,可以通過研究對象特殊位置的處理找出正確的結論,再由特殊拓展至一般情況,在科學論證的基礎上得出最終結論.

圖5
分析:題中動點P的任意性使得|OP|、|AQ|、|AB|都是處于變化之中,題目中要證明的定值結論,這里可以采取特殊狀態確定這一定值,即將P點移動至A′點,則|OP|= a,|AQ|=2a,|AB|=a,則知道定值結果心中就踏實多了,再將P點移動至其他一般位置進行證明,在證明過程中就存在著目標性,這樣解題能夠做到胸有成竹、游刃有余.
思考:本題中采取特殊化探路、一般化解決的處理手段,體現了人類認識客觀世界的基本規律,這也是探究數學規律的重要形式之一,動態的一般性問題利用靜態下的特殊狀態進行試探,為成功解題奠定基礎;學生的創新思維在動靜轉換中得以激發和提升,有助于培養學生在處理數學問題中化歸思想的運用意識.
總而言之,高中數學的解題過程是一個系統的工作,化歸思想作為數學解題的思想方法其實施途徑是多樣化的,“化高為低、化虛為實、化整為零……”都是我們解題中常用的方法,作為一線的高中數學教師,在平時的教學中注重引導學生對化歸途徑的有效探尋,讓學生在探尋中發揮自身的創新思維,激發對數學學習的興趣,進一步提升分析問題和解決問題的創造性能力.F

