讓思維與能力的翅膀在復(fù)習(xí)課中飛揚(yáng)

☉江蘇省天一中學(xué) 何志奇

☉江蘇省無(wú)錫市錫山區(qū)教研室姚敬東

·江蘇省無(wú)錫市何志奇名師工作室·

讓思維與能力的翅膀在復(fù)習(xí)課中飛揚(yáng)

☉江蘇省天一中學(xué) 何志奇

☉江蘇省無(wú)錫市錫山區(qū)教研室姚敬東

2015年元月15號(hào)，筆者應(yīng)邀為云南省普洱市的老師與同學(xué)開(kāi)設(shè)了一節(jié)必修五的“數(shù)列”一章的復(fù)習(xí)課，平生第一次為云南的孩子上課，感慨頗多，記錄點(diǎn)滴，與同行一起交流和分享.

一、注重通性通法，給學(xué)生留有思維的空間

復(fù)習(xí)題講解要注意“變化”.對(duì)于復(fù)習(xí)課例題的選擇，應(yīng)突出教材重點(diǎn)選擇具有典型性的題目，能反映教學(xué)大綱中最主要的、最基本的要求.在對(duì)例題進(jìn)行分析解答后，應(yīng)注意發(fā)揮例題的示范功能，力求在例題的基礎(chǔ)上進(jìn)一步變化，把平時(shí)所學(xué)的零散知識(shí)“集中裝箱”，形成良好的認(rèn)知結(jié)構(gòu).對(duì)復(fù)習(xí)課教學(xué)，我們應(yīng)當(dāng)考慮如何讓學(xué)生動(dòng)起來(lái)，為他們創(chuàng)造比較多的交流機(jī)會(huì).真正讓學(xué)生動(dòng)起來(lái)，需要教師精心設(shè)計(jì)教學(xué)環(huán)節(jié)，建構(gòu)科學(xué)的結(jié)構(gòu)，為不同的學(xué)生留出層次各異的思維空間，達(dá)到最大限度地發(fā)展學(xué)生能力的目的，這是我們應(yīng)當(dāng)重點(diǎn)考慮的問(wèn)題.

復(fù)習(xí)時(shí)不必拘于環(huán)節(jié)設(shè)計(jì)，要關(guān)注針對(duì)性、隨機(jī)應(yīng)變性，以解決問(wèn)題為主，對(duì)學(xué)生暴露出來(lái)的問(wèn)題對(duì)癥下藥.因?yàn)閷W(xué)生的問(wèn)題是形形色色的，不以教師意志為轉(zhuǎn)移的，因此預(yù)先設(shè)計(jì)好的環(huán)節(jié)恐怕與學(xué)生當(dāng)時(shí)暴露出來(lái)的問(wèn)題不一致.

片斷1：設(shè)等差數(shù)列｛an｝的前n項(xiàng)和為Sn，Sm-1=-2，Sm= 0，Sm+1=3，則m=_________.

本題難嗎？不難，等差數(shù)列中，有三個(gè)條件足夠了，題目條件正好給出，還有什么難解決的呢？筆者讓學(xué)生練習(xí)這道題，收獲是很大的.

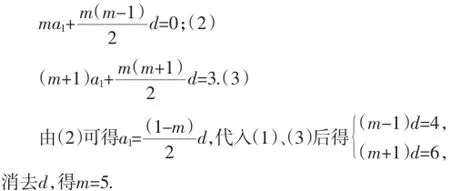
點(diǎn)評(píng)：屬于用基本量法解決問(wèn)題，學(xué)生應(yīng)該都可以掌握的.

生2：由Sm-1=-2，Sm=0，可得am=2，由Sm+1=3，Sm=0，可得am+1=3，從而d=1，以下同生1的解法.

點(diǎn)評(píng)：巧用性質(zhì)，靈活處理，該方法屬于最佳解法.

生3：利用等差數(shù)列的前n項(xiàng)和公式Sn=an2+bn，注意到Sm=0，由二次函數(shù)圖像的對(duì)稱性，可知函數(shù)f（x）=ax2+ bx一定過(guò)點(diǎn)（1，-2），（-1，3）.

點(diǎn)評(píng)：這類同學(xué)具有數(shù)形結(jié)合的思想，而且始終把數(shù)列看成是特殊的函數(shù)，因此解決起來(lái)就會(huì)得心應(yīng)手，游刃有余.

對(duì)于不給學(xué)生時(shí)間，教師注入式的復(fù)習(xí)，更是不可取的，教師“一言堂”的復(fù)習(xí)，雖然表面上教學(xué)目的達(dá)到了，但實(shí)際上沒(méi)有落實(shí).因?yàn)闊o(wú)論基礎(chǔ)知識(shí)、基本技能、思想方法、能力培養(yǎng)都必須經(jīng)過(guò)學(xué)生親身實(shí)踐和體驗(yàn)，才能領(lǐng)會(huì)和理解，光靠教師的講授、歸納提升，并不能落到實(shí)處.

二、注重例題的透徹解析，深化學(xué)生的思維層次

解題思路要注意“優(yōu)化”.在復(fù)習(xí)中，必須注意題目解法的多樣性，善于比較、提煉出最佳解法，從而達(dá)到優(yōu)化解題思路的目的.這種復(fù)習(xí)，在活躍學(xué)生思維的同時(shí)，也讓學(xué)生在解答的過(guò)程中充分體驗(yàn)到成功的愉悅，從而培養(yǎng)了復(fù)習(xí)數(shù)學(xué)的興趣.習(xí)題歸類要注意“類化”.在復(fù)習(xí)中，教師要善于引導(dǎo)學(xué)生將習(xí)題分類歸檔，并集中力量解決同類題中的本質(zhì)問(wèn)題，總結(jié)出解決這類問(wèn)題的方法和規(guī)律，真正讓學(xué)生跳出“題海”.通過(guò)一系列的歸類訓(xùn)練，學(xué)生便能把解題的方法從一個(gè)問(wèn)題遷移到另一個(gè)問(wèn)題，從而達(dá)到舉一反三、觸類旁通的效果.運(yùn)用知識(shí)要注意“深化”.學(xué)習(xí)的目的在于應(yīng)用，數(shù)學(xué)教學(xué)必須要聯(lián)系生活實(shí)際，培養(yǎng)學(xué)生能夠運(yùn)用數(shù)學(xué)知識(shí)解決簡(jiǎn)單的實(shí)際問(wèn)題，在復(fù)習(xí)中，應(yīng)有目的地精選一些與所學(xué)數(shù)學(xué)知識(shí)聯(lián)系密切的實(shí)際問(wèn)題，使學(xué)生在解答過(guò)程中受到學(xué)以致用的良好熏陶，從而達(dá)到運(yùn)用知識(shí)的“深化”.

片斷2：已知數(shù)列｛an｝的前n項(xiàng)和Sn滿足Sn+Sm=Sn+m，且a1=1，那么a10=_________.

生5：因?yàn)镾2=a1+a2=2S1，所以a2=1；因?yàn)镾3=S1+S2=3，所以a3=1；因?yàn)镾4=S1+S3=4，所以a4=1，……同理，a10=1.

總結(jié)：由特殊到一般.

生6：取m=1，則有Sn+S1=Sn+1，所以Sn+1-Sn=S1=a1=1，可知數(shù)列｛Sn｝是以S1為首項(xiàng)，公差為1的等差數(shù)列.所以Sn= S1+（n-1）d=1+（n-1）=n，故a10=S10-S9=10-9=1.

總結(jié)：由特殊到一般，再到特殊.

生7：取m=1，n=9，得S9+S1=S10，所以a10=S10-S9=S1=a1=1.

總結(jié)：特例開(kāi)路，多思少算，注重思維.

三、注重方法能力的培養(yǎng)，讓學(xué)生的個(gè)性化思維得到彰顯

對(duì)新穎的信息、情境和設(shè)問(wèn)，選擇有效的方法和手段分析信息，綜合與靈活地應(yīng)用所學(xué)的數(shù)學(xué)知識(shí)、思想和方法，進(jìn)行獨(dú)立的思考、探索和研究，提出解決問(wèn)題的思路，創(chuàng)造性地解決問(wèn)題.創(chuàng)新意識(shí)是理性思維的高層次表現(xiàn).對(duì)數(shù)學(xué)問(wèn)題的觀察、猜測(cè)、抽象、概括、證明，是發(fā)現(xiàn)問(wèn)題和解決問(wèn)題的重要途徑，對(duì)數(shù)學(xué)知識(shí)的遷移、組合、融會(huì)的程度越高，顯示出的創(chuàng)新意識(shí)也就越強(qiáng).復(fù)習(xí)課要更加側(cè)重于能力和思維，使通過(guò)死記硬背、題海戰(zhàn)術(shù)等方式獲取高分將越來(lái)越困難.這也是推行素質(zhì)教育，減輕學(xué)生負(fù)擔(dān)的一種體現(xiàn)，其背后的教育目的是更加注重培養(yǎng)學(xué)生個(gè)性化的思維能力、自己解決問(wèn)題的能力.通過(guò)新題型的變化，逐步淘汰被人長(zhǎng)久詬病的“填鴨式”教學(xué).當(dāng)然，傳統(tǒng)的教學(xué)還不能一棒子打死，在沒(méi)有找到一種能夠廣泛引導(dǎo)、訓(xùn)練學(xué)生這種思維能力、自己解決問(wèn)題的能力之前，當(dāng)前數(shù)學(xué)教學(xué)方面，題海戰(zhàn)術(shù)還是有一定的生存空間.筆者認(rèn)為，既然暫時(shí)不能拋棄這種教學(xué)，但在日常教學(xué)中留給一定的時(shí)間，引導(dǎo)學(xué)生多思考、多交流，少些埋頭蠻干，是能逐步適應(yīng)高考課改的.

片斷3：數(shù)列｛an｝是等差數(shù)列，若a1+1，a3+3，a5+5構(gòu)成公比為q的等比數(shù)列，則q=_________.

師：大家對(duì)這道題先思考，然后與周圍的同學(xué)交流一下自己的想法.

生8：因?yàn)閿?shù)列｛an｝是等差數(shù)列，所以利用an=a1+（n-1）d，使得a3、a5都用a1與d來(lái)表示，根據(jù)a1+1，a3+3，a5+5成公比的關(guān)系式（a3+3）2=（a1-1）（a5-5），求出a1與d，代入a3+ 3，a5-5得出q的值.

師：非常好.利用基本元：首項(xiàng)與公差，解決公比q.有沒(méi)有對(duì)這個(gè)解法有新的認(rèn)識(shí)？

生9：我的想法是把a(bǔ)1用a3-2d、a5用a3+2d來(lái)表達(dá)，利用a3-2d-1，a3+3，a3-2d+5成公比，先求出a3，……

師：有沒(méi)有更好的解法，來(lái)優(yōu)化上面這些同學(xué)的解法？老師提示一下，大家想一想，如果一個(gè)數(shù)列既是等差數(shù)列又是等比數(shù)列，那么這個(gè)數(shù)列肯定是一個(gè)特殊的數(shù)列，請(qǐng)問(wèn)：特殊在哪里？你能否舉一個(gè)例子？

生10：1，2，3……

師：它是等比數(shù)列嗎？不要緊張，沒(méi)有想好？沒(méi)有關(guān)系，慢慢想，后面的女生，您說(shuō)說(shuō)看呢？

生11：an=1，就是1，1，……

師：非常好，很優(yōu)秀.還有嗎？

生12：2，2，2，……

師：很好，不錯(cuò).

生13：a，a，a，……

師：非常好！您比前面的同學(xué)回答的更一般化了，大家明白了嗎？這道題應(yīng)該很容易解決了，q是多少？（眾答：q=1）正確，q=1，a1+1，a3+3，a5+5很明顯既是等差數(shù)列又是等比數(shù)列.不動(dòng)筆動(dòng)動(dòng)腦就拿下了.因此，拿到一個(gè)題目，從解題的大框架著手，怎么想解題思路很重要.本題給你這樣一個(gè)強(qiáng)烈的印象：復(fù)習(xí)時(shí)，拿到題目不要馬上去做，先要想一想怎么思考，如何優(yōu)化自己的解法.

讓學(xué)生講并不是把課堂完全交給學(xué)生，學(xué)生只是一個(gè)環(huán)節(jié)一種方式，學(xué)生的講解往往帶有片面和不簡(jiǎn)潔的特點(diǎn)，老師先要對(duì)學(xué)生的講解進(jìn)行鋪墊，讓聽(tīng)的學(xué)生做好準(zhǔn)備，中間還要針對(duì)聽(tīng)的學(xué)生可能產(chǎn)生的問(wèn)題適時(shí)對(duì)講解的學(xué)生進(jìn)行提問(wèn)和提示，或允許聽(tīng)眾進(jìn)行提問(wèn)，最后還要組織總結(jié)和點(diǎn)評(píng).這樣聽(tīng)的學(xué)生是從自己的角度去聽(tīng)，聽(tīng)得細(xì)，聽(tīng)得明白，講的同學(xué)也會(huì)有所收獲.

這點(diǎn)實(shí)際上要注意的是，只有在前面著力引導(dǎo)學(xué)生對(duì)自己的學(xué)習(xí)情況有一個(gè)比較清楚的把握的基礎(chǔ)上，引起他們對(duì)自己的知識(shí)缺失點(diǎn)或困惑點(diǎn)的足夠重視，學(xué)生講也好，老師講也好，這樣他們才會(huì)有共同學(xué)習(xí)的興趣，才會(huì)有效果.學(xué)生講的是他自己對(duì)學(xué)習(xí)這一點(diǎn)知識(shí)的經(jīng)驗(yàn)體會(huì)和方法，講的是一個(gè)小點(diǎn)，一個(gè)可以啟發(fā)大家，供大家學(xué)習(xí)的地方；或者是講自己的困惑，這樣以引起有共同問(wèn)題的同學(xué)的注意.

部分老師在提問(wèn)時(shí)多數(shù)時(shí)候是讓優(yōu)秀生講，時(shí)間長(zhǎng)了，其他學(xué)生會(huì)認(rèn)為這件事與自己無(wú)關(guān)，也就沒(méi)有參與的熱情了，對(duì)于借班上課的老師來(lái)說(shuō)一般是不存在這樣的問(wèn)題的.

四、注重?cái)?shù)學(xué)素養(yǎng)的提高，培養(yǎng)學(xué)生的邏輯推理與計(jì)算能力

我們?cè)跀?shù)學(xué)復(fù)習(xí)時(shí)，除抓好知識(shí)、題型、方法等方面的教學(xué)外，還應(yīng)通過(guò)各種方式、機(jī)會(huì)提高和規(guī)范學(xué)生的運(yùn)算能力和邏輯推理等能力.細(xì)心審題、耐心答題，規(guī)范準(zhǔn)確，減少失誤.計(jì)算能力、邏輯推理能力是考試大綱中明確規(guī)定的兩種培養(yǎng)的能力.可以說(shuō)是學(xué)好數(shù)學(xué)的兩種最基本能力，在數(shù)學(xué)試卷中的考查無(wú)處不在.并且在每年的閱卷中因?yàn)檫@兩種能力不好而造成的失分占有相當(dāng)大的比例.

片斷4：甲、乙兩廠2013年元月份的產(chǎn)值相等，甲廠產(chǎn)值逐月增加，且每月增加的產(chǎn)值相同，乙廠產(chǎn)值也逐月增加，且每月增加產(chǎn)值與上月產(chǎn)值的百分比相同，若2014年元月份甲、乙兩廠的產(chǎn)值又相等，則2013年7月份甲、乙兩廠產(chǎn)值的大小關(guān)系是_________.

生14：由題意可知甲、乙兩廠的月產(chǎn)值分別構(gòu)成等差數(shù)列｛an｝和等比數(shù)列｛bn｝，且a1=b1及a13=a1+12d=b13=b1q12，a7＞b7.

生15：由上述方法知an=a1+（n-1）d是關(guān)于n的一次函數(shù)，bn=a1qn-1是關(guān)于n的指數(shù)型函數(shù)，由圖1可知，當(dāng)1＜n＜13，均有an＞bn，顯然，結(jié)論很明白了.

復(fù)習(xí)課內(nèi)容的重點(diǎn)永遠(yuǎn)是基礎(chǔ).要通過(guò)對(duì)基礎(chǔ)題的系統(tǒng)訓(xùn)練和規(guī)范訓(xùn)練，準(zhǔn)確理解每一個(gè)概念，能從不同角度把握所學(xué)的每一個(gè)知識(shí)點(diǎn)、所有可能考查到的題型，熟練掌握各種典型問(wèn)題的通性、通法.復(fù)習(xí)一定要做到細(xì)且實(shí)，切不可因輕重不分而出現(xiàn)“前緊后松，前松后緊”的現(xiàn)象，也不可因趕進(jìn)度而出現(xiàn)“點(diǎn)到為止，草草了事”的情況，只有真正實(shí)現(xiàn)讓思維在碰撞中激發(fā)，實(shí)施自主學(xué)習(xí)，才能真正達(dá)到復(fù)習(xí)的目的.F

圖1