小學數學教師要學點邏輯知識
——例談邏輯思維的三種形式

馮回祥

小學數學教師要學點邏輯知識
——例談邏輯思維的三種形式

馮回祥

小學數學教師為什么要學點邏輯知識？因為數學教學就是數學思維教學，其關鍵就是讓學生掌握概念、判斷和推理的方法，提高學生的思維能力。作為教師，對數學知識、數學問題不僅要知其然，還要知其所以然，這也是對教師的專業要求。同時，學習邏輯是信息時代的需要，面對各種各樣的信息，需要人們正確地進行判斷和推理，作出決策。最后，良好的邏輯思維是形成批判性思維的核心基礎。如果一個人的邏輯思維較差，要他具備批判性思維那是不現實的。因此，要培養學生的批判性思維，教師自己必須具備批判性思維的素養，那么掌握一定的邏輯知識就成為了必然。

普通邏輯學涉及到的內容和方法較為廣泛，需要系統的學習。根據小學數學教學的實際需要，筆者認為，在以下幾個方面要重點學習。比如了解什么是邏輯學，什么是思維。其中比較重要的是了解思維最基本的三種形式：概念、批判和推理。

第一，了解什么是概念。概念是反映事物本質屬性的思維形式。

屬性，分本質屬性和非本質屬性。本質屬性是指能與其他事物相區別的屬性；非本質屬性不是事物獨有的屬性。例如，“有一個公共端點的兩條射線組成的圖形”是“角”這個事物獨有的屬性，即“角”的本質屬性。由這個屬性可以把“角”和其他圖形區別開。但“位置的不同”卻不是“角”所獨有的，是“角”的非本質屬性。

概念的內涵與外延。內涵是指一個概念所概括的思維對象本質屬性的總和。外延是指一個概念所概括的思維對象的數量或范圍，它是一些具體的事物。例如：“商品”這一概念的內涵是，為了交換而生產的勞動產品。而這個概念的外延是市場上的汽車、房子、食品等等。又如：“質數”的概念的內涵是，“只有1和它本身兩個因數”，它的外延是2，3，5，7等一切具體的質數。概念的內涵與外延是概念質和量的兩個方面。了解概念的內涵與外延，對于人們正確地理解概念、準確地運用概念，具有重要意義。若我們掌握了某一概念的內涵與外延，則這個概念就是明確的；反之，就是對這一概念沒有掌握或沒有完全掌握。因此，掌握一個概念的內涵與外延的程度是衡量我們對概念明確到什么程度的標準。由于概念的種類較多，概念間也存在著許多關系，需要我們慢慢去了解。

怎樣給概念下定義，下定義時必須遵守哪些規則？

一是定義的內涵。定義是通過簡明的陳述以揭示概念內涵或外延的邏輯方法，也就是通過指出概念所反映事物的本質屬性來明確概念的邏輯方法。

例如：（1）一個數中每一個數字所占的位置叫做數位。

（2）“≥”叫做大于或等于號。

定義由被定義項、定義項和定義的聯項三部分組成。

被定義項，是需要加以說明的概念。如上例中“數位”和“≥”。

定義項，是用來明確被定義項的概念。如上例中“一個數中每一個數字所占的位置”和“大于和等于的符號”。

定義聯項，是用來聯合被定義項和定義項的語詞。如上例中的“叫做”。

二是定義的方法。定義的方法有多種，與小學數學相關的有：

屬加種差法。在給一些具有屬種關系的種概念下定義時，首先指出被定義的概念最鄰近的屬概念是什么，再確定在這個屬里它與其他種概念的差別（簡稱“種差”），從而對概念下定義，通常把這種定義方法叫屬加種差法。其結構是：鄰近的屬概念+種差=被定義概念。例如：兩組對邊分別平行（種差）的四邊形（屬）叫做平行四邊形（被定義概念）。

屬加種差法所下的定義一般不是唯一的，在同一數學體系中一般只能采用一個定義，其他可以由所給的定義推出，作為性質定理處理。

外延定義法。在給一個已知各個種概念下定義時，通常列出這些種概念給這個屬概念下定義，這種定義方法稱為外延定義。

例如：（1）有理數和無理數統稱為實數。

（2）整數和分數統稱為有理數。

約定式定義法。根據數學上某種特殊需要，通過約定的方式來下定義。例如：為了實際計算的需要，規定a×1=a，a×0=0，0／a=0（a≠0），a／1=a。約定式定義所作的規定，都不是憑主觀臆造的，而是以符合客觀規律為基礎的。

三是定義的規則。給概念下定義有嚴格規則，否則就會犯邏輯錯誤。

規則一，定義應當是相稱的。這就是說定義項的外延與被定義項的外延應當全同，違反這一規則就犯了“定義過寬”或“定義過窄”的邏輯錯誤。例如：（1）無限小數是循環小數（定義過寬——定義項的外延大于被定義項的外延）；（2）四邊和四角皆相等的四邊形叫做矩形（定義過窄——定義項的外延小于被定義項的外延）。

規則二，定義不應當是循環的。這是說在給概念下定義時，不能用被定義項來說明自己。違反這一規則就犯了“循環定義”的邏輯錯誤。例如：乘法是幾個數相乘的方法。

規則三，定義應當簡單明確。這就是說定義項應當明白、確切，不應含糊不清，也不能用比喻。違反這一規則就犯了“定義不清”或“以比喻代定義”的邏輯錯誤。例如：（1）正方形是有規則的四邊形。（2）像足球那樣的幾何體叫球。

規則四，定義一般不采取否定式。這條規則的要求是除了給否定概念下定義以外，定義項一般不用否定概念，也不用否定判斷下定義。違反這條規則就犯了“定義否定”的邏輯錯誤。例如：梯形是非兩組對邊平行的四邊形。

第二，什么是判斷。人們建立了許多概念以后，就可以應用這些概念去判定客觀事物的情況。對客觀事物有所判定的思維形式叫做判斷。判定事物具有某種屬性，是肯定；判斷事物不具有某種屬性，是否定。例如：正方形是特殊的長方形為肯定；梯形不是平形四邊形是否定。判斷可分為簡單判斷和復合判斷兩種。

1.簡單判斷，是指不包含其他判斷的判斷。這種判斷又分為兩種：（1）性質判斷，是判定事物具有或不具有某種性質的判斷。例如：“3是奇數”，“有些自然數不是偶數”，“所有分數都能化成小數”，這都是性質判定。（2）關系判斷，是指判定事物間關系的判斷。例如：有的角大于直角；大于1。

2.復合判斷，是包含其他判斷的判斷。這種判斷包含幾種情況：（1）聯言判斷，是判定幾種事物情況共存的判斷。例如：1既不是質數，又不是合數。（2）選言判斷，是判定可能有的幾種事物情況的判斷。例如，這個數被4除余數是0，或是1，或是2，或是3；一個自然數要么是偶數，要么是奇數，（3）假言判斷，是判定一種事物情況為另一種事物情況的條件的判斷。如，如果a×b=1，那么a和b成反比例；只有x≠0時，才能使1/x有意義。（4）多重復合判斷，是由復合判斷組成的判斷。如，7248的末尾數8能被2整除，而不能被5整除，所以7248是2的倍數而不是5的倍數。

第三，什么是推理。即由一個或幾個已知的判斷（命題），推出一個新的判斷（命題）的思維形式。例如：

（1）∵長方形的面積=長×寬，長方形的長是5厘米，寬是3厘米。

∴長方形的面積是5×3=15（平方厘米）。

推出一般結果：

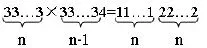
推理包含前提和結論兩個部分。前提是已知的判斷，是推理的出發點和根據。結論是由前提而推出新的判斷，是推理的結果。由于結論是由前提推斷出來的新判斷，因此，在推理中有“推出關系”，沒有推出關系的一些判斷的堆積，不是推理。例如：（1）偶數2是質數，所以有的偶數是質數；（2）5是自然數，7是自然數；（3）所有自然數是整數，2+5＞6，3是質數。其中例（1）有推理關系，可以組成推理（當然是個錯誤的推理），例（2）不具有推理關系，例（3）幾個判斷之間沒有邏輯關系，所以他們不能組成推理。

判斷具有真假性，因此由已知判斷推出的新判斷（即推理）也有真假性。一般來說，“如果前提為真，推理正確，結論也必然為真；如果前提為真，推理錯誤，結論就可真可假；如果前提為假，推理正確，結論也可真可假”。從一個前提出發，經過某種推理，得出一個假的判斷，那么可以判斷前提為假，或者推理錯誤。例如：

（1）∵有些奇數是9的倍數，有些質數是奇數

∴有些質數是9的倍數

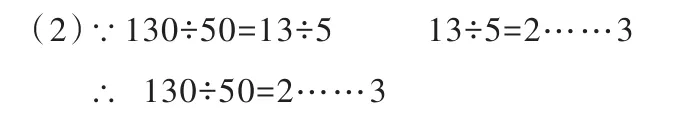
例（1）（2）盡管前提都是真實的，但由于推理不合乎邏輯規則和邏輯規律，因此得到的結論是錯誤的。

推理這種思維形式有重要的作用，它是我們獲取新知識（間接地）以及說明和論證問題的重要手段。

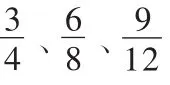
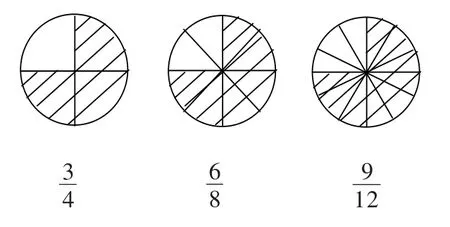
再運用這個判斷進行推理，可得：分數的分子和分母都乘或者除以相同的數（零除外），分數的大小不變。

其次，推理是解答、論證問題的重要手段。

綜上不難看出：概念是組成判斷的要素，判斷則是概念的繼續和展開，是對概念的說明。判斷是組成推理的成份，沒有判斷，就不會有推理，就不會對事物有所判定，也就談不上認識客觀世界。

學習邏輯知識，掌握邏輯方法，提升自身的綜合素養，是時代對我們的要求。高素質的教師，是培養和發展學生的思維能力和創新意識的重要基礎，也是提高教育質量的基本保障。

（作者單位：華中科技大學附屬小學）

責任編輯 嚴 芳

“我的信息化教學”征文評獎活動啟事

湖北歷來十分重視利用信息技術促進教育公平，提高教育質量，培養創新人才，帶動產業發展。經過十余年的發展，已經具備了一定基礎，并于2014年1月獲批在全國率先開展教育信息化省級試點。目前，湖北省教育信息基礎設施得到較大改善，優質數字教育資源不斷豐富，信息化教學不斷深入。

信息化教學，是以現代教學理念為指導，以信息技術為支持，應用現代教學方法的教學。它不僅是課堂教學方式的改變，更注重對學習環境的整體設計，強調在課程觀指導下整合各種資源來支持“學”，培養學生信息素養，優化教育過程。

2015年，本刊編輯部將以“我的信息化教學”為題舉辦征文評獎活動，為您提供展示的平臺。

一、征文要求

1.參評文章需緊扣“我的信息化教學”這一主題，結合教育教學實踐，體現您自身的思考，做到敘述生動、分析深入、邏輯清晰。

2.征文題目自擬，文體不限，可以是論文、敘事、隨筆等，字數控制在3500字以內。

3.征文請以附件形式發送到電子信箱hbjyzwhd@163.com，并留下詳細的通信地址、聯系方式。

4.活動截止時間是2015年12月31日。

二、評選與表彰

1.征文截止后，本刊將組織專家集中評審，擬評出特等、一等、二等獎各若干名，并頒發獲獎證書。為表彰積極組織參加征文活動的各級教育管理、教研部門及學校，特設組織獎若干名。

2.特別優秀的參評文章，本刊將開辟專欄予以發表，其他優秀文章也可免費結集出版。

3.征文評審費每篇80元，評審費請通過郵局寄至：武漢市洪山區珞喻路78號長江傳媒大廈19樓《湖北教育》編輯部。

《湖北教育》編輯部

2014年12月31日