兆瓦級風力機塔架的有限元非線性屈曲分析
唐瑞宏, 湯赫男, 許增金, 王世杰
(1.沈陽工業大學 機械工程學院,沈陽 110870;2.沈陽鼓風機集團風電有限公司,沈陽 110869)
0 引言
我國風能資源豐富,近幾年風電事業得到長足發展,但我國風力機設備制造,設備利用率和風力機基礎設計等一系列技術問題還有待于進一步解決。其中,最亟待解決的是塔架損壞的問題,據不完全統計,在諸多風力機的損壞形式中,塔架的折斷占到了18%,位居各項破壞形式之首,這說明目前塔架的設計還存在缺陷。塔架是風力機重要的承載部件,它除了支撐風力機的重量之外,還要承受風壓力和風力機運行中的動載荷。塔架可以近似看成一種細長體薄壁結構,在軸向壓力的作用下易發生屈曲失穩,設計時必須特別關注其穩定性。研究塔架穩定性問題,需要借助于有限元屈曲分析方法。屈曲分析是用于確定結構處于失穩臨界狀態時的屈曲載荷和屈曲模態的一種技術手段。ANSYS中提供了兩種進行屈曲分析的方法:線性(特征值)屈曲分析和非線性屈曲分析。線性屈曲分析即傳統的理想線彈性屈曲分析方法,然而非理想和非線性行為阻止了實際結構達到該理論極限載荷預計的階段,故線性屈曲分析會產生非保守的結果。而非線性屈曲分析可以得到更精確的屈曲載荷,是打開大變形效應開關的一種靜力分析,考慮結構的初始缺陷和材料非線性等特性。非線性屈曲分析提取線性屈曲分析結果作為非線性屈曲的幾何缺陷,然后逐漸對結構加載,該過程一直進行到結構的極限載荷或最大載荷為止。研究塔架穩定性的目的在于確定塔架在軸向壓力作用下的臨界載荷及其相應的屈曲模態,以加強安全措施,提高結構的抗失穩能力[3]。本文借助于 ANSYS12.0有限元軟件,對2MW78m風力機塔架進行非線性屈曲分析,分析塔架門對塔架穩定性的影響。
1 塔架有限元模型的建立與加載
1.1 單元類型的選擇
SHELL93為8節點彈性殼單元,可以很好地模擬曲殼,該單元的每個節點有6個自由度,即沿節點坐標系x、y和z方向的平動位移和繞各軸的轉動位移[1],采用殼單元SHELL93模擬塔架結構,分為是否存在塔架門的兩種類型,分別對塔架進行有限元屈曲分析計算。
1.2 塔架參數
塔架為圓筒形式,是目前風力機普遍采用的典型結構形式。該塔架的高度為78 m,最大壁厚為30 mm,最小壁厚為12 mm,塔底外徑為2.15 m,塔頂外徑為1.477 5 m。材料為Q345鋼,屈服強度為345 MPa,泊松比為0.2,彈性模量為2.1×1011Pa,材料密度為7 850 kg/m3。
1.3 加載方案
有限元分析的關鍵問題在于將實際工程系統的物理模型轉化為相應的數學模型。風力機塔架內部設有一些附屬設備:如平臺、爬梯、通風口等。有限元分析時,可以對塔架幾何模型作適當簡化,原則是在保證整體計算精度的前提下,簡化一些與塔架穩定性分析無關或承載非關鍵的部位,以提高計算速度。
坐標原點在塔架底部中心處,Z軸正向為垂直底面向上。塔架底端全約束,頂端施加方向沿Z軸反方向的單位載荷,塔架整體受重力作用,重力加速度為-9.8 m/s2。其中有塔架門模型的單元數為4 572個,節點數為13 650個。有塔架門的殼單元塔架的有限元模型,如圖1所示。

圖1 有塔架門的殼單元塔架的有限元模型
2 有限元屈曲分析
2.1 經典ANSYS非線性屈曲分析過程
1)打開預應力開關選項,進行線性屈曲分析;
2)設置幾何缺陷,逐漸對結構加載;
3)采用線性搜索方法,進行非線性屈曲分析;
4)結果后處理,建立載荷和位移關系曲線,確定結構的非線性臨界載荷。

圖2 無塔架門線性屈曲第一階等效應力圖

圖3 有塔架門線性屈曲第一階等效應力圖
2.2 屈曲有限元結果分析及校核
2.2.1 線性屈曲結果分析
打開預應力開關選項,進行線性屈曲分析。由線性屈曲分析結論可知,無塔架門線性屈曲第一階特征值是0.499 02×108,而有塔架門線性屈曲第一階特征值是0.494 39×108。從計算結果中可以看出:無塔架門線性屈曲特征值大于有塔架門線性屈曲特征值,這說明無塔架門的塔架穩定性優于有塔架門的塔架,即塔架門的存在會降低塔架抵抗屈曲失穩的能力。無塔架門線性屈曲第一階等效應力圖,如圖2所示。有塔架門線性屈曲第一階等效應力圖,如圖3所示。
2.2.2 強度校核
通過ANSYS后處理功能,可直觀形象地將塔架的強度分析結果表示出來,如圖2、圖3所示。
強度檢驗條件:σmax<[σ],其中σmax為計算出的最大應力,[σ]為材料許用安全應力。塔架材料的屈服極限σs=345 MPa,則其許用應力為:[σ]=σs/n,n 為材料的安全系數。根據 GL規范,n=1.1,則[σ]=313.6 MPa。其中ANSYS計算出的無塔架門塔架的最大應力值小于許用應力,強度滿足設計要求;有塔架門塔架的最大應力值大于許用應力,強度不滿足設計要求,需考慮門框加強設計。
2.2.3 非線性屈曲結果分析
1)無塔架門塔架非線性屈曲結果分析。由線性屈曲分析結論可知,無塔架門線性屈曲的載荷因子達到0.499 02×108時發生屈曲,對于非線性屈曲,載荷因子達到0.48×108時發生屈曲,選取應力最大節點776號位移載荷圖,如圖4所示。非線性屈曲因子小于線性屈曲因子,非線性屈曲結果更為保守。
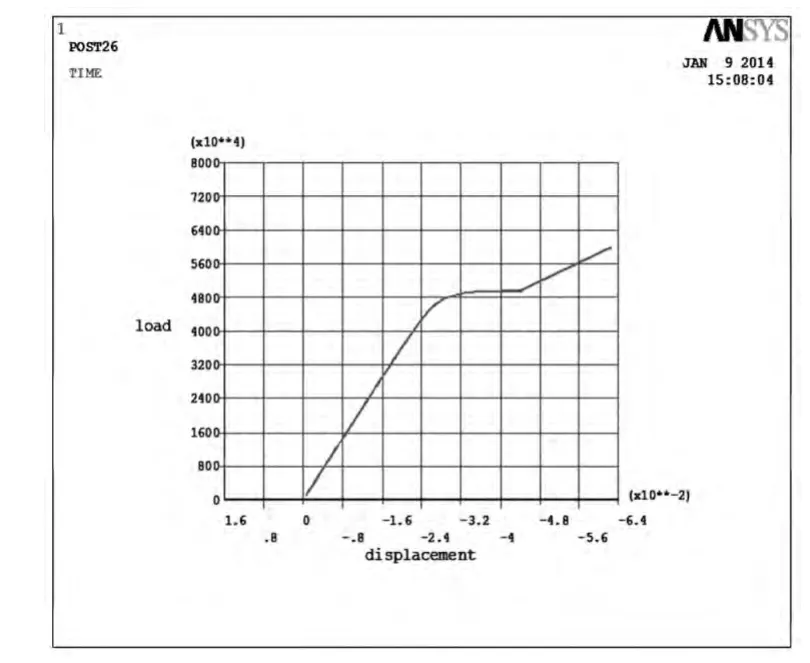
圖4 節點776號位移載荷圖

圖5 節點32號位移載荷圖
2)有塔架門塔架非線性屈曲結果分析。由非線性屈曲分析結論可知,有塔架門塔架線性屈曲的載荷因子達到0.494 39×108時發生屈曲,對于非線性屈曲,載荷因子達到0.46×108時發生屈曲,選取應力最大節點32號位移載荷圖,由圖5所示。非線性屈曲因子小于線性屈曲因子,同樣產生保守結果。
2.2.4 分析結果比較
不論是線性屈曲分析,還是非線性屈曲分析,得到的結果都是無塔架門塔架的第一階屈曲載荷值大于有塔架門塔架的第一階屈曲載荷值,塔架門會降低塔架的屈曲臨界載荷值,即降低同種工況下塔架抵抗屈曲失穩的能力,需特別關注塔架門附近的應力并考慮門框加強設計。
塔架穩定性取決于其一階屈曲臨界載荷,塔頂端的葉輪和機艙的總重力為1.18 MN,極限工況下的軸向壓力為1.056 2 MN,合力為2.236 2 MN。取經典ANSYS有塔架門的非線性屈曲結果為例,屈曲因子為非線性屈曲特征值與合力的比,約為20,根據IEC標準,對曲線外形件的綜合彎曲,如管狀塔架和葉片,屈曲因子大于1.2就不會發生屈曲失穩。該塔架的穩定性滿足設計要求,不會發生屈曲失穩。
3 結論
本文采用有限元ANSYS軟件的非線性屈曲分析方法,對2MW78m風力機薄壁塔架進行了有限元屈曲分析,研究風力機在軸向壓力作用下的塔架門對塔架屈曲的影響。塔架門的存在會降低塔架屈曲特征值,降低同種工況下塔架抵抗屈曲失穩的能力。有塔架門塔架的最大應力點出現在塔架門附近,應力最大位置是發生屈曲失穩的危險點,需進行強度校核,但強度不滿足設計要求,的考慮門框加強設計。
[1] 朱仁勝,劉永梅,蔣東翔,等.基于MW級風力發電機塔架的有限元分析[J].機械設計與制造,2011,5(5):104-106.
[2] 高耀東,宿福存,李震,等.ANSYS Workbench機械工程應用精華30例[M].北京:電子工業出版社,2013.
[3] 趙世林,李德源,黃小華.風力機塔架在偏心載荷作用下的屈曲分析[J].太陽能學報,2010(7):901-906.
[4] 黃國良,嚴峰.基于有限元法的框架式壓縮機基礎動力分析[J].風機技術,2011(3):15-19.
[5] 王慧慧,黃方林,吳合良,等.風力發電機塔架的有限元分析[J].山東交通學院學報,2009(6):63-67.
[6] 王新敏,李義強,許宏偉.ANSYS結構分析單元與應用[M].北京:北京人民交通出版社,2012.
[7] Germanischer Lloyd Windengergie GmbH.Guideline for the certification of wind turbines[S].
[8] International Electrotechnical Commission.International Standard IEC 61400-1-2005 Wind Turbines[S].
[9] 湯煒梁,袁奇.大型風力機塔筒三維有限元分析[J].電力技術,2010(5):59-63.

