基于有限元方法的汽車驅動橋殼分析
吳超 廖敏 業紅玲

驅動橋橋殼作為汽車的重要承載和傳力部件,其強度和動態性能直接影響汽車運行的安全、平順性和舒適性。本文運用有限元法研究了驅動橋殼在最大鉛垂力工況下的靜力分析,得出了驅動橋殼強度和變形符合要求;同時對驅動橋殼進行模態分析得出了驅動橋殼前六階固有頻率并給出了前四階模態振型,分析結果表明橋殼結構合理。上述研究得出的結論為后續驅動橋殼的優化和實驗提供了重要的參考依據。
作為汽車總成的重要組成部件,驅動橋殼支撐著汽車的質量,并將載荷傳給車輪。汽車在行駛過程中由于載荷作用產生振動,驅動橋殼振動特性直接影響驅動橋本身的振動和整車行駛的平穩性。因此對驅動橋殼結構的研究很有必要。文中利用有限元法進行靜力分析和模態分析,為后續的動力學響應分析提供了參考指導。
一、驅動橋殼有限元分析方法
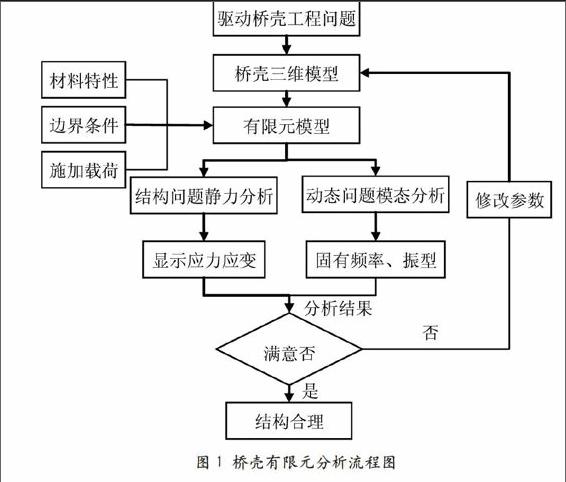
以計算機和矩陣運算為基礎的有限元法是對復雜工程問題或結構問題計算的近似的數值分析方法。驅動橋殼需要有很大的強度和剛度,驅動橋殼傳統的經驗設計方法是利用數學、力學等理論知識進行計算。這種方法計算量大且很復雜,很難模擬各種工況。根據汽車驅動橋殼的結構、各種受力和約束,應用有限元法模擬,可以計算出驅動橋系統的動態響應,結果可信且接近實際,能較真實地模擬出驅動橋動態使用過程。圖 1是汽車驅動橋殼有限元分析流程。
首先要建立驅動橋殼的三維數值模型,結合橋殼的材料及屬性轉化為有限元分析模型,對有限元模型添加約束邊界并施加載荷,然后計算求解,進行驅動橋殼的結構靜力分析和動力學模態分析,通過有限元后處理分析結果可分別獲得驅動橋殼的應力和變形、固有頻率和振型,結合材料特性和使用要求進行驅動橋殼的強度和剛度判斷,從而為改進和優化驅動橋殼設計提供可靠的數據支持。
二、驅動橋殼有限元模型建立
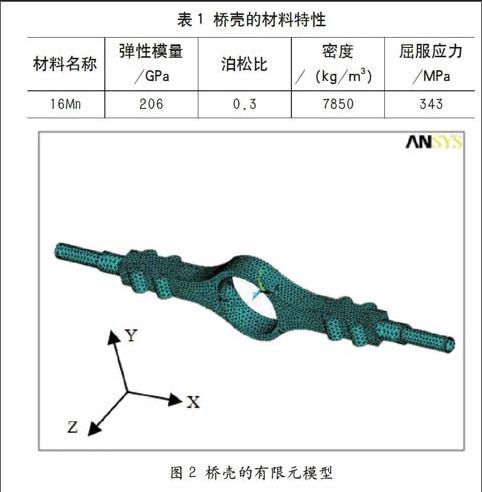
在 NX軟件中建立某型汽車驅動橋殼的三維模型,由于汽車驅動橋橋殼結構形狀較為復雜,包含許多復雜曲面。在保證不影響求解精度的前提下,對幾何模型進行一定的簡化。對主要承載件,均保留其原結構形狀,以反映其力學特性,對非承載件進行一定程度的簡化或忽略,可以忽略不重要的小尺寸和小孔結構。然后將驅動橋殼輸出為Parasolid數據格式,經 ANSYS的 Parasolid接口導入進行分析。本文劃分網格時選用四面體 10節點 Tet solid92實體單元(四面體 10節點單元具有較高的剛度及計算精度),賦予其單元材料為 16Mn,材料屬性詳細參數如表 1所示。通過有限元網格劃分得到 20745個單元,41090個節點。圖 2是劃分網格的有限元分析模型。
三、驅動橋殼的有限元分析
1.驅動橋殼的靜力分析
驅動橋殼是汽車重要的承重件,在路面凹凸不平時,將會受到路面沖擊載荷的作用,這時鉛垂力最大(即沖擊載荷)。不考慮驅動橋殼所受的側向力、切向力和彎矩的作用,取 2.5倍的靜載荷平均施加在兩個板彈簧座上。橋殼的相關數據:驅動橋滿載后軸荷為 3.2t,簧距 800mm,輪距 1240mm。
G×δ mg×δ
F垂 =F靜 ×δ = 2 =2
式中, G是汽車在靜止情況下驅動橋給路面的載荷; δ為動載荷系數,通常情況下取 2.5; g為重力加速度,其值為 9.8m/s 2;m為驅動橋滿載軸荷。經計算得 F垂=39200N。
橋殼的載荷約束條件:橋殼輪距處兩平面固定,板簧上施加鉛錘力,具體條件如表 2所示,載荷約束方式如圖 3所示,求解后得到橋殼的等效位移云圖和應力云圖,如圖 4和圖 5所示。
(1)變形分析。
從圖 4位移云圖可知橋殼在沖擊載荷作用下最大變形發生在橋殼的中央處,其最大位為 0.736mm。根據國家標準,每米輪距橋殼最大變形量不超過 1.5mm,承受 2.5倍滿載軸荷時,橋殼不能出現斷裂和塑性變形。橋殼的每米變形 0.736/1.240<1.5符合國家要求。
(2)應力分析。
從圖 5應力云圖可知在沖擊載荷作用下其最大應力值為 248MPa,發生在橋殼兩端附近,大部分部位應力值在 27MPa~ 82MPa之間。其值小于橋殼材料的許用應力343MPa,橋殼的強度符合要求。
根據以上結論可知,該橋殼在沖擊載荷作用下的強度和變形均符合要求。
2.驅動橋殼的模態分析
一般多自由度運動學微分方程為:
式中, M、C、K為系統的質量、阻尼和剛度矩陣;為系統的加速度、速度和位移; F(t)為外激勵向量。
經傅立葉變換可得無阻尼模態分析求解的基本方程為:
式中,[ K]為剛度矩陣;{Φ i}為第 i階模態振型向量; ωi為第 i階模態固有頻率;[ M]為質量矩陣。
模態分析是研究振動的主要手段。模態分析的主要的目的是為了識別出系統的模態參數,為結構系統的振動特性分析,振動故障診斷及預報以及結構動力特性優化設計提供依據。驅動橋殼模態分析可以識別出其結構的固有頻率以及固有振型,不僅對于防止汽車發生共振等情況具有指導作用,而且模態動態性能也是驅動橋殼結構動力響應分析的基礎。
ANSYS 軟件模態提取方法有Block Lanczos(分塊藍索斯法)、Subspace(子空間法)、Reduced(縮減法)和Unsymmetrical Method(非對稱法)等6 種。本文使用ANSYS 模態分析方法中的Block Lanczos 法模態提取法。Block Lanczos 法采用了稀疏矩陣求解法,故其收斂速度更快,求解效率更高。在ANSYS 軟件中計算得到的前6 階模態下的固有頻率值(表3)。同時圖6 ~圖9 給出了對應于前4 階模態固有頻率的振型。
由于結構的振動可以表達為各階固有振型的線性組合,其中低階自振頻率所引起的共振往往引起結構較大的應變和應力,高階的影響則很小,因此低階振型決定了結構的動態特性,從振型顯示結果中更容易看出各階振動的方向和相對幅值大小。
具有代表性的第二和第四階振型。橋殼第二階振型表現為整體沿 Y軸的一階垂向彎曲,第四階振型表現為整體沿 Y軸的二階垂向彎曲,這種振動方式與汽車行駛輪胎上下顛簸一致,在凹凸不平地面時容易引起共振發生殼體破壞。
橋殼第一階振型表現為整體沿 Z軸的縱向彎曲,殼體的中部腔體振動明顯,加劇差速器齒輪嚙合磨損。
橋殼第三階振型表現為整體沿 X軸的扭轉,將會減弱傳動軸剛度,影響傳遞的扭矩。
從整體的模態分析結果可知橋殼的各階固有頻率較為分散,相鄰階次不會同時引起共振。汽車在不平的路面行駛,汽車振動系統承受路面作用的激勵多屬于 1Hz~ 50Hz垂直振動。驅動橋殼的第一階固有頻率大于激勵頻率,橋殼不會因共振而使結構破壞。
四、結語
通過運用 CAD/CAE軟件對汽車驅動橋殼進行分析,可以降低開發成本,減少實驗次數,具有實際意義。本文對驅動橋殼進行靜力分析,經仿真得到結果為結構合理性驗證提供了有力的條件。由模態分析可知,橋殼的各階模態大于路面的激勵頻率,不會產生共振,同時為以后驅動橋殼的振動試驗和優化做了一定的基礎。endprint

