磚墻抗爆炸沖擊震動效應模型試驗研究

李利莎，張洪海，謝清糧，杜建國

(總參工程兵科研三所，河南洛陽 471023)

磚墻抗爆炸沖擊震動效應模型試驗研究

李利莎，張洪海，謝清糧，杜建國

(總參工程兵科研三所，河南洛陽 471023)

為研究磚墻在爆炸沖擊震動作用下的破壞模式及閾值，據工程內磚墻實際情況建立簡化的底部固定、周邊無約束磚墻模型，在模擬爆炸震動沖擊試驗臺上進行三方向單獨作用的沖擊試驗，研究磚墻模型的動態響應及破壞時加速度峰值、作用時間。結果表明，遭水平向沖擊時模型均表現為水平通縫破壞。破壞主要由受拉而非剪切所致。通過對試驗結果分析，獲得三個沖擊方向獨立作用下的破壞閾值。

磚墻;爆炸沖擊震動;模型試驗;破壞閾值

磚墻廣泛用于建筑物外墻及內部分割空間的非承重墻主要承受壓力作用，抗拉、抗彎、抗剪強度較低，因此拉力、剪力作用易導致結構松散而毀壞。資料表明［1－3］，在觸地核爆或地下封閉核爆時，雖防護工程主體完好，但爆炸產生的地沖擊震動仍十分強烈，能引起防護工程內部磚隔墻倒塌及儀器設備等損壞。隨爆破施工日益頻繁，由爆破所致地震效應通常也會引起磚墻開裂、甚至倒塌。因此，研究爆炸沖擊震動對磚墻安全性影響意義重大。

磚墻、砌體結構的破壞研究主要集中于抗地震、抗爆炸空氣沖擊波領域［4－6］，而對抗爆炸震動［7－10］則主要通過對爆破拆除、民用開采、隧道開挖等工程的大量震動測量結果的研究與分析，認為在瞬態爆炸震動作用下工程結構破壞主要因素為質點速度。因此，普遍采用速度作為爆破地震危害判據;但將地面質點速度作為結構破壞的唯一判據并不準確，因其未考慮結構固有特性如自振頻率及震動信號頻率特性等，而此特性對結構動態響應同樣關鍵。Dowding等［10］研究表明，結構反應與頻率相關性較大，并通過實例說明質點速度峰值接近兩波形(爆炸A為3.8×10－3m/s、爆炸B為3.3×10－3m/s)產生的結構響應相差較大，即在民房及組成部分自振頻率5～20 Hz范圍內，爆炸B產生的結構響應約為爆炸A的10倍。

本文通過研究，以期弄清磚墻在爆炸震動作用下的破壞模式，探索爆炸震動對磚墻的破壞機理，給出磚墻的破壞閾值，為工程結構的爆炸震動防護設計提供參考。

1 試驗概況

1.1 試驗設備

室內沖擊試驗在總參工程兵科研三所大型沖擊模擬試驗臺上進行，試驗裝置［11］見圖1。該裝置模擬原理為:爆炸產生的震動與爆炸方式、當量、侵入深度、介質狀況、結構埋深等多種因素有關，雖震動信號各不相同，但對效應物的作用相同。若將多自由度系統效應物簡化為具有相同阻尼比的多個單自由度系統，爆炸震動對效應物的作用效果與對各單自由度系統作用效果相同時可對爆炸震動加速度信號進行反應譜分析，用半正弦加速度脈沖反應譜包絡，則半正弦脈沖加速度值即為爆炸震動的等效加速度值，半正弦脈沖作用時間即為爆炸震動加速度等效作用時間，使爆炸震動對效應物作用統一衡量尺度，因此爆炸震動模擬與對效應物的作用效果等效。由沖擊試驗機產生的近似半正弦脈沖加速度信號可通過調整沖擊加速度值及作用時間實現對爆炸震動模擬。

圖1 爆炸震動模擬沖擊試驗臺Fig.1 Shock testing machine for simulating blast

試驗臺工作原理為由沖擊氣壓推動沖擊錘撞擊臺體產生一定加速度模擬核爆炸及常規武器爆炸震動環境。沖擊臺面面積1.7 m×1.2 m，最大負荷20 kN，沖擊加速度峰值范圍為5～200 g，脈沖作用時間5～45 ms，沖擊方向為垂直、水平。試驗中通過調整沖擊氣壓及墊層厚度改變沖擊加速度峰值及主脈沖寬度。

1.2 磚墻模型形狀選取

對一間房間或相鄰房間而言，可認為爆炸沖擊對磚墻產生整體震動，墻體與其連接墻體共同運動時，不但承受自身振動荷載，亦將承受其它墻體荷載，因此不能簡單簡化為單面墻;受條件限制，不能進行一排磚墻模型試驗，只能選典型部分進行重點研究。因此，試驗模型設計時將整體磚墻拆分為連續的“工”字形單元，研究該單元在沖擊荷載作用下的動力響應，每個“工”字形單元在爆炸震動作用下整體振動。因沖擊臺承載能力有限，磚墻模型加各連接件重量已接近其承載能力上限，不能通過在磚墻模型上施加質量建立考慮重力加速度等效的人工質量等效比例模型;亦不能在翼墻兩側施加約束(因加約束的連接件需足夠剛度，若滿足一定剛度要求，整個模型重量超出沖擊臺承載能力，只能進行理論簡化)。故選兩種底部固定、周邊無約束的“工”字形截面模型，研究其三方向受沖擊震動作用的動態響應。

1.3 模型試驗比例系數

進行室內沖擊試驗時選1∶2忽略重力加速度等效比例模型。據相似律［12］結構模型相似比例系數見表1。

表1 模型試驗相似系數Tab.1 Similarity coefficients of model experiment

1.4 磚墻模型

選兩種“工字形”磚墻比例模型見圖2。其中兩翼墻長×寬×高≈600 mm×118 mm×1 000 mm、中間橫墻長×寬×高≈1 082 mm×118 mm×1 000 mm(稱長模型)見圖2(a);兩翼墻長×寬×高≈600 mm×118 mm×1 000 mm、中間橫墻長×寬×高≈882 mm×118 mm×1 000 mm(稱短模型)見圖2(b)。該模型為磚墻簡化比例模型，在翼墻處未加任何約束。試驗用小磚由強度等級為MU10的普通燒結粘土磚經機械切割而成，1塊原磚切成8塊試驗磚，三方向對半切割，切割后外形尺寸平均118 mm×55 mm×24 mm，砂漿縫控制在4～5 mm，磚墻模型平均密度1 651 kg/m3。模型底座由14a#槽鋼與5#角鋼焊接成工字型，并在槽鋼內澆注鋼纖維混凝土，見圖2(c)，兩邊槽鋼長度均為1 000 mm，兩邊槽鋼中心線相距分別為1 200 mm、1 000 mm，兩種模型底座平均重量分別為65 kg、61 kg。

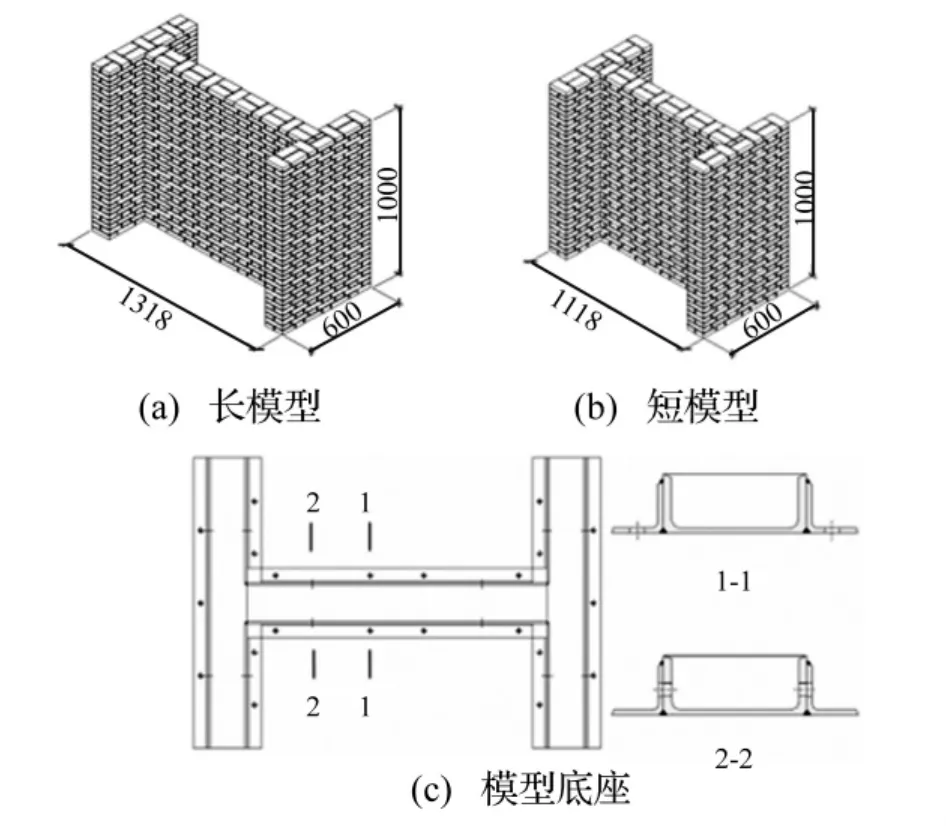
圖2 磚墻模型及模型底座示意圖Fig.2 Masonry wall model and model base

2 試驗結果與分析

2.1 縱向水平沖擊試驗及分析

縱向水平方向進行3組共9個模型沖擊試驗，沖擊方向平行于磚墻模型中間橫墻軸線，安裝、沖擊方向及加速度測點位置見圖3，磚墻采用長模型，各組之間砂漿強度稍有差別。測試沖擊臺體、連接鋼板等處沖擊加速度及磚墻動應變、墻頂加速度等參數。每個模型均由小沖擊震動輸入開始，通過調整沖擊氣壓及墊層厚度改變沖擊加速度峰值及主脈沖寬度，記錄每次沖擊加速度等參數及模型宏觀破壞現象，直至磚墻模型完全破壞。

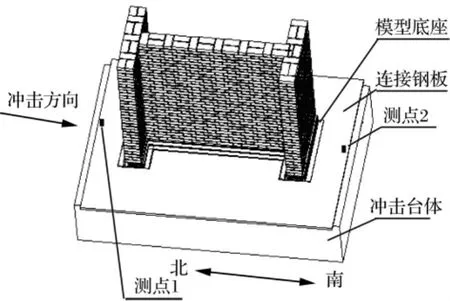
圖3 縱向水平沖擊試驗模型安裝及測點布置圖Fig.3 Model installation and measuring point arrangement in the longitudinal horizon shock experiment

篇幅所限，只選典型的第2組3個模型試驗進行介紹，該組模型砂漿強度4.77 MPa，自振頻率約67 Hz (垂直沖擊方向基頻)、138 Hz(平行沖擊方向基頻)。2－4#模型共進行8次沖擊試驗，第5次沖擊時模型南翼墻東側底部附近出現可見細縫;2－5#模型共進行7次沖擊試驗，第5次沖擊時宏觀未見細縫，但據加速度等信號的嚴重異常判斷模型此時已產生局部破壞;2－6#模型共進行3次沖擊試驗，第2次沖擊時模型南翼墻東側底部附近見細縫，與2－4#模型相似。

該組3個模型宏觀破壞現象一致。完全破壞時裂縫均出現在底部第1、2皮磚之間，向南部滑移距離稍不同，2－4#向南滑移約25～30 mm，2－5#向南滑移約70～80 mm，2－6#向南滑移約27～28 mm。該組模型在正向加速度作用下首先在最南端底部第1、2皮磚之間拉裂，隨沖擊臺繼續運行裂縫越來越大，破壞的部分墻體被拉高，底部裂縫迅速向另側發展，基本已擴展到另側翼墻處;由于負向加速度作用，南端一側被拉裂墻體下落，此時最北端墻體在底部第1、2皮磚間拉裂，裂縫增大，該側墻體被拉起，裂縫向另側發展形成通縫，導致模型整體破壞。此時沖擊臺體已處于負向加速度狀態，即向前運行速度逐漸減小，因此完全拉裂墻體將以破壞時初速度在兩者交界面上繼續向前滑行，完全破壞時向前初速度不同致3個模型向前滑移距離不同。模型完全破壞時典型的宏觀破壞見圖4，鋼板南端加速度及模型宏觀破壞見表2。

圖4 縱向水平沖擊試驗模型破壞情況Fig.4 Failure of models in the olngitudinal horizon shock experiment

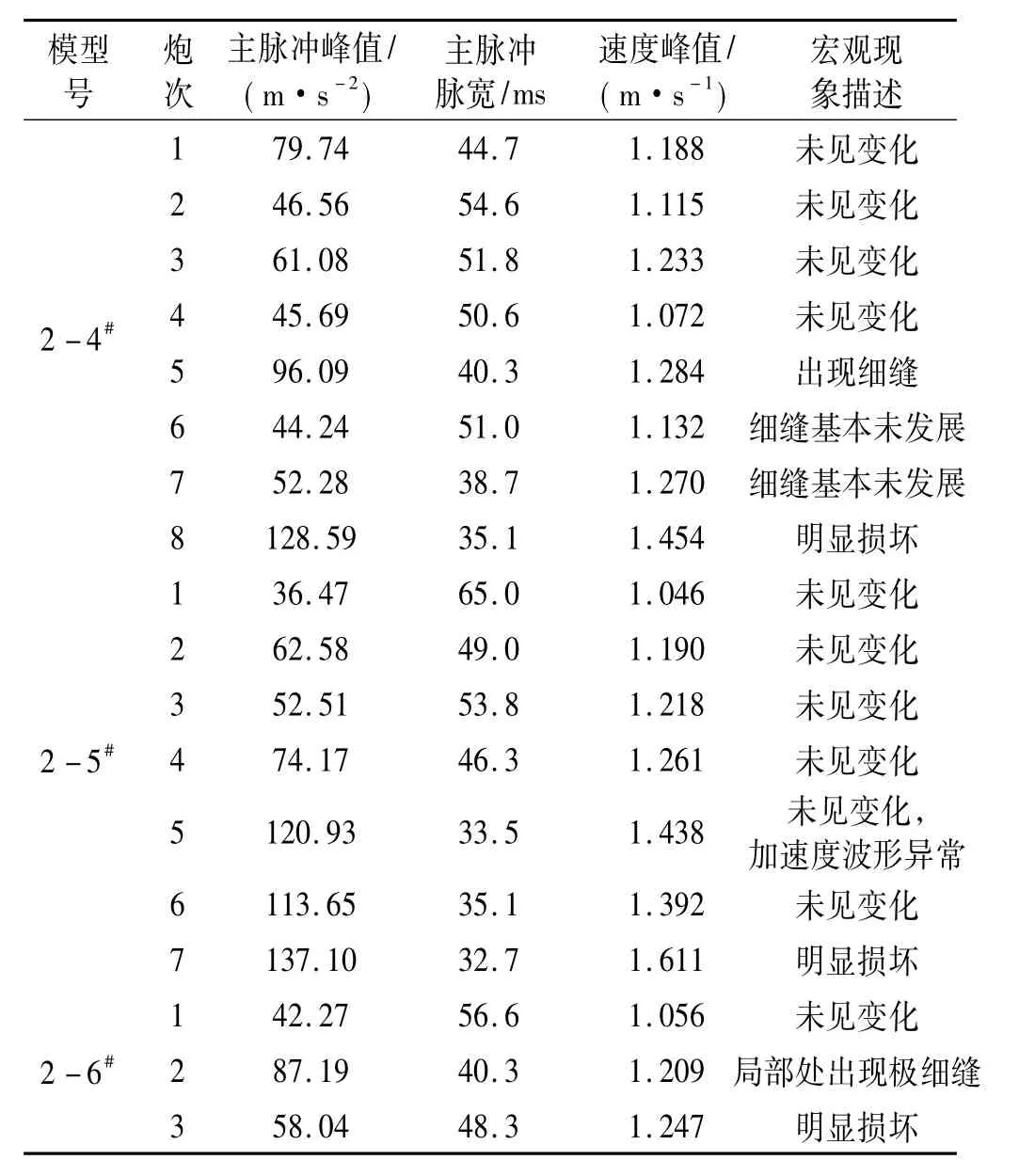
表2 縱向水平沖擊試驗第2組加速度參數及宏觀破壞現象Tab.2 Acceleration parameters and macroeconomic failure of the 2nd group in the longitudinal horizon shock experiment

典型的加速度信號見圖5。由圖5(b)看出，2－5#模型在第4次沖擊時加速度信號仍正常，而第5次沖擊時加速度波形類似圖5(a)，產生嚴重異常，在峰值處存在明顯突變現象，即反方向大幅回落，由波形判讀可知，2－4#模型在第5次沖擊時產生局部破壞。

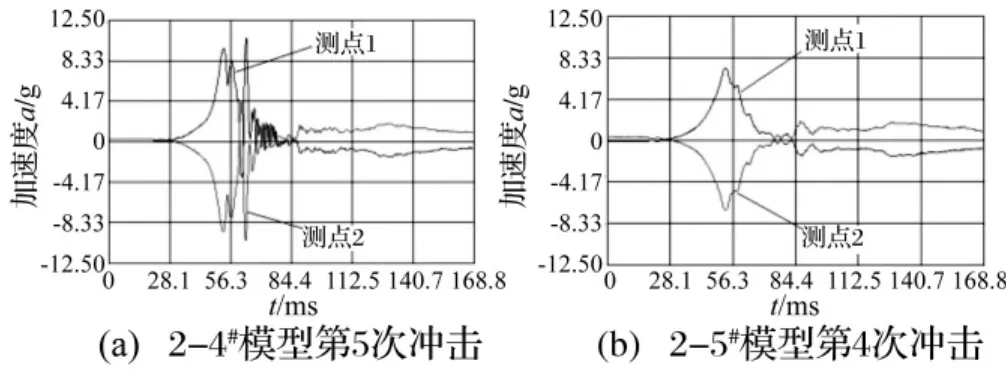
圖5 縱向水平沖擊試驗加速度信號Fig.5 Acceleration signals in the longitudinal horizon shock experiment

2.2 橫向水平沖擊試驗及分析

磚墻采用短模型進行1組3個模型的水平沖擊試驗。模型編號1－1#～1－3#;沖擊方向由北向南垂直中間橫墻軸線水平，安裝、沖擊方向及加速度測點見圖6。模型砂漿強度4.20 MPa，自振頻率分別為74.30 Hz (平行沖擊方向基頻)及128.40 Hz(垂直沖擊方向基頻)。

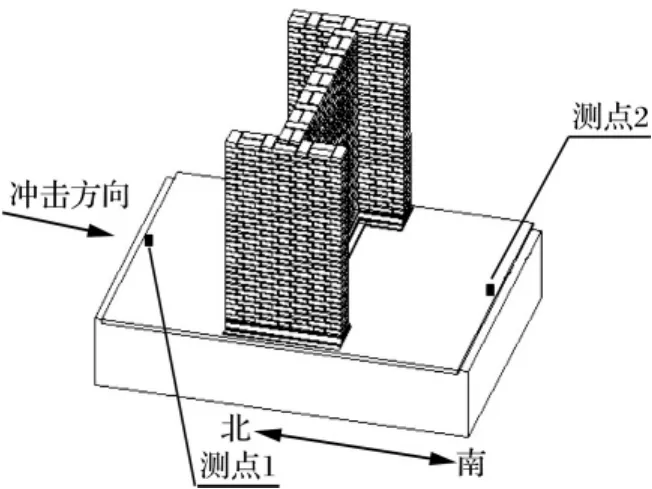
圖6 橫向水平沖擊試驗模型安裝及測點布Fig.6 Model installation and measuring point arrangement in the transversal horizon shock experiment

3個模型均只進行1次沖擊試驗，其中1－1#模型在吊裝過程中西翼墻南端局部已出現可見細縫，位于模型第2、3皮磚之間。由于3個模型破壞過程類似，此處僅介紹1－1#。西翼墻最南端第2、3皮磚之間首現受拉斷裂，裂縫繼續向北發展，翼墻破壞已超過橫墻，橫墻西側出現裂縫，南側墻體拉起;南側墻體下落兩翼墻在最北端第2、3皮磚之間拉裂并向南發展，西側翼墻已產生貫通性裂縫，脫離底部向南滑移，東側翼墻未產生貫通性裂縫，中間橫墻整體破壞，整個模型以東翼墻南端為中心向南偏東方向轉動;北側墻體落下，南側墻體重新被拉起。1－1#及1－2#模型整體破壞狀態見圖7，橫向水平沖擊試驗加速度及模型宏觀破壞現象見表3。

圖7 橫向水平沖擊試驗模型破壞情況Fig.7 Failure of models in the transversal horizon shock experiment

橫向水平沖擊試加速度測試信號見圖8。由圖8看出，1－1#模型在加速度峰值附近測試信號出現異常，而1－2#模型則分別在21 m/s2、29 m/s2附近加速度出現異常。在橫向水平沖擊震動作用下翼墻底部拉裂破壞對沖擊臺反作用較小，因此模型拉裂部分被拉起時引起的波形異常不及縱向水平沖擊模型時劇烈。由此，經對加速度波形的判讀可認為1－1#模型在接近加速度峰值時產生破壞，而1－2#則在21.0～29.0 m/s2附近產生破壞。

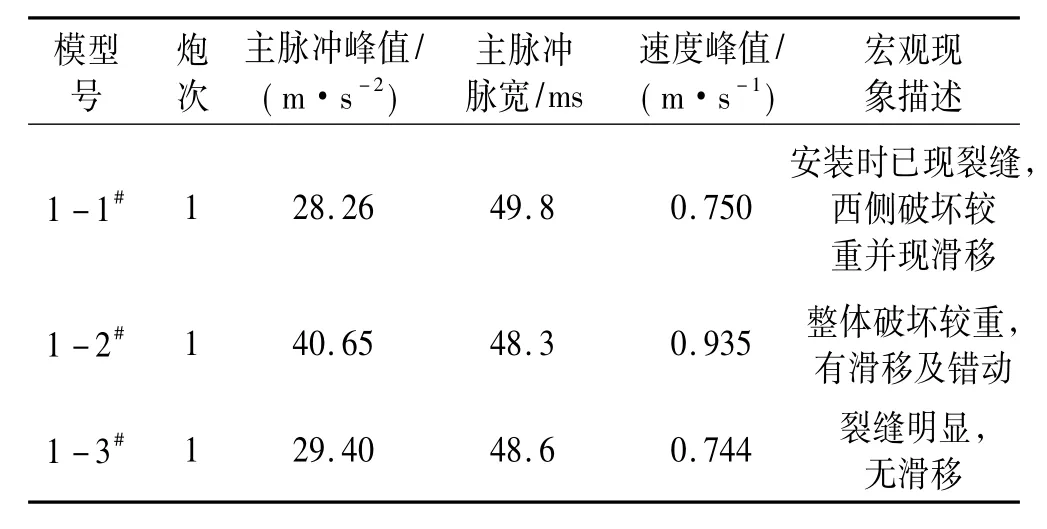
表3 橫向水平沖擊試驗加速度參數及宏觀破壞現象Tab.3 Acceleration parameters and macroeconomic failure in the transversal horizon shock experiment

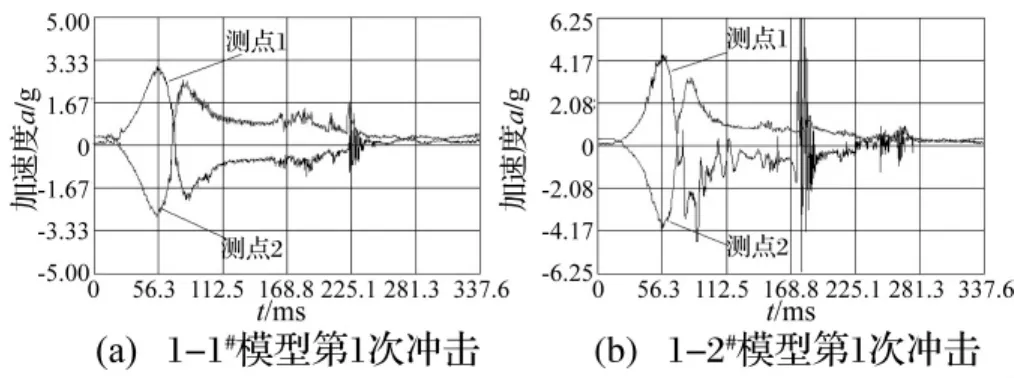
圖8 橫向水平沖擊試驗加速度信號Fig.8 Acceleration signals in the transversal horizon shock experiment

2.3 垂直沖擊試驗及分析

垂直方向進行2組共6個模型試驗，安裝及沖擊方向見圖9，其中磚墻用短模型。

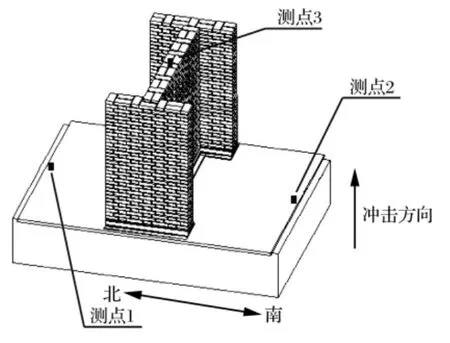
圖9 垂直沖擊試驗模型安裝及測點布置Fig.9 Model installation and measuring point arrangement in the vertical shock experiment

現只介紹第2組編號2－1#～2－3#模型。3個模型砂漿強度均4.77 MPa，垂向自振頻率為330 Hz。2－1#模型進行2次沖擊試驗。安裝時東翼墻底部1、2皮磚之間局部已現細縫，第1次沖擊后原裂縫繼續擴展，第2次沖擊時模型整體沿1、2皮磚間脫離，并向東滑移約4 cm。2－1#第2次向上沖擊過程中，模型與沖擊臺呈西高東低現象，先在原有裂縫處拉裂并迅速整體拉裂;隨沖擊臺向上速度降低及下落，完全拉裂的墻體部分與其它部分脫離并高高拋起，上部斷裂墻體下落后東端先接觸下部底座;上部斷裂墻體下落后南北向來回晃動明顯。斷裂墻體下落時整體向東移動，完全破壞狀態見圖10(a)。2－2#模型共進行4次沖擊試驗，前3次模型無明顯宏觀破壞，第4次沖擊時模型在底部1、2皮磚(局部在2、3皮磚)之間破壞，東翼墻向南滑移約1.4 cm，西翼墻南側無滑移現象，整體以西翼墻南側為軸有水平轉動跡象，整體破壞狀態見圖10(b)。2－3#模型亦進行4次沖擊試驗。第2次沖擊時模型西翼墻南側及中間橫墻南側面西部1、2皮磚之間已現極細裂縫;第3次沖擊時底部1、2皮磚之間已現水平通縫;第4次沖擊時模型在底部1、2皮磚之間完全脫離，向南滑移約2.3 cm，并伴有向東南方向輕微轉動，整體破壞狀態如圖10(c)。2－2#模型第4次加速度信號見圖11。

圖10 垂直沖擊試驗模型破壞情況Fig.10 Failure of models in the vertical shock experiment

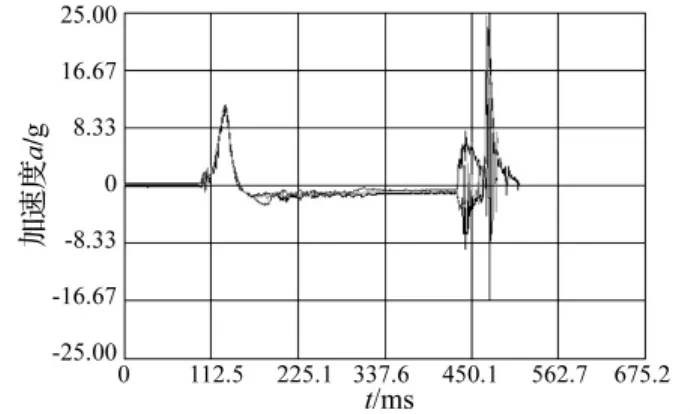
圖11 垂直沖擊試驗2－2#模型第4次的加速度信號Fig.11 Acceleration signals of the 4th of model 2－2#in the vertical shock experiment

垂直沖擊試驗第2組加速度及破壞見表4。由表4看出，若不考慮撞擊加速度，模型承受的加速度峰值并不大。正向最大加速度峰值為112.70 m/s2，此時模型底部壓應力最大，但較磚墻模型抗壓強度該應力水平太小，不足以使模型受壓破壞;同樣負向加速度峰值最大不超過35 m/s2，此時底部拉應力最大，即使加上整個模型因臺體傾斜轉動產生的拉應力，該應力水平也不會引起磚墻模型的受拉破壞。因此可認為垂直向上的沖擊試驗并未使磚墻模型破壞，唯一引起模型破壞的原因為沖擊臺連磚墻模型與沖擊臺基座碰撞。

為研究臺體與基座碰撞加速度，進行垂直向沖擊第3組3個模型試驗，記錄的碰撞加速度波形見圖12。臺體與基座碰撞瞬間臺體加速度見表5。由表5看出，臺體碰撞時產生的負向加速度較大。實測臺體加速度波形位于沖擊臺南端東西方向中心處，由于沖擊過程中臺體呈明顯的西高東低現象，使碰撞時臺體東西兩端加速度峰值較中心處實測加速度峰值大。

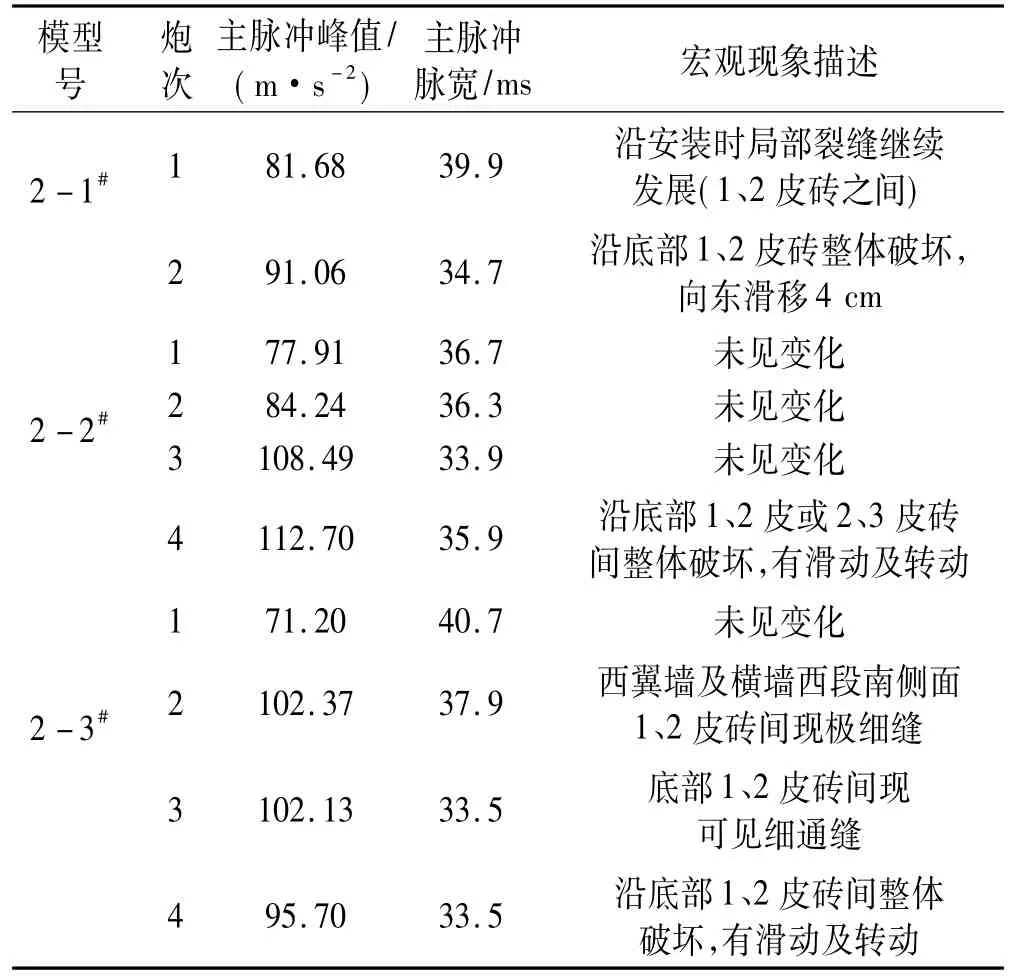
表4 垂直沖擊試驗第2組加速度參數及宏觀破壞現象Tab.4 Acceleration parameters and macroeconomic failure of the 2nd group in the vertical shock experiment

由于臺體傾斜程度不同，其間比例亦不相同，無法通過碰撞時臺體南端中央處加速度峰值計算臺體其它位置加速度峰值，較難給出模型在瞬時垂直向加速度作用下準確的破壞極限;考慮磚墻模型整體轉動影響，據試驗結果認為模型做垂直沖擊試驗時在臺體碰撞過程中由于負向加速度及模型轉動影響引起拉裂破壞，對應的參考加速度峰值約－200 m/s2。

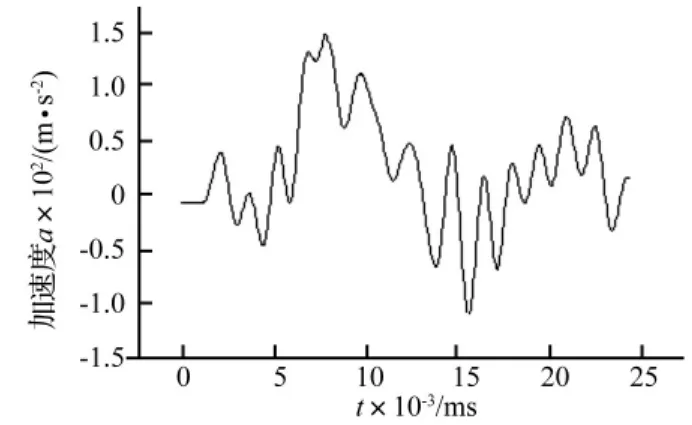
圖12 垂直沖擊試驗3－1#模型第1次臺體撞擊加速度信號Fig.12 Acceleration signals of the 1st of model 3－1#at the moment of impaction in the vertical shock experiment

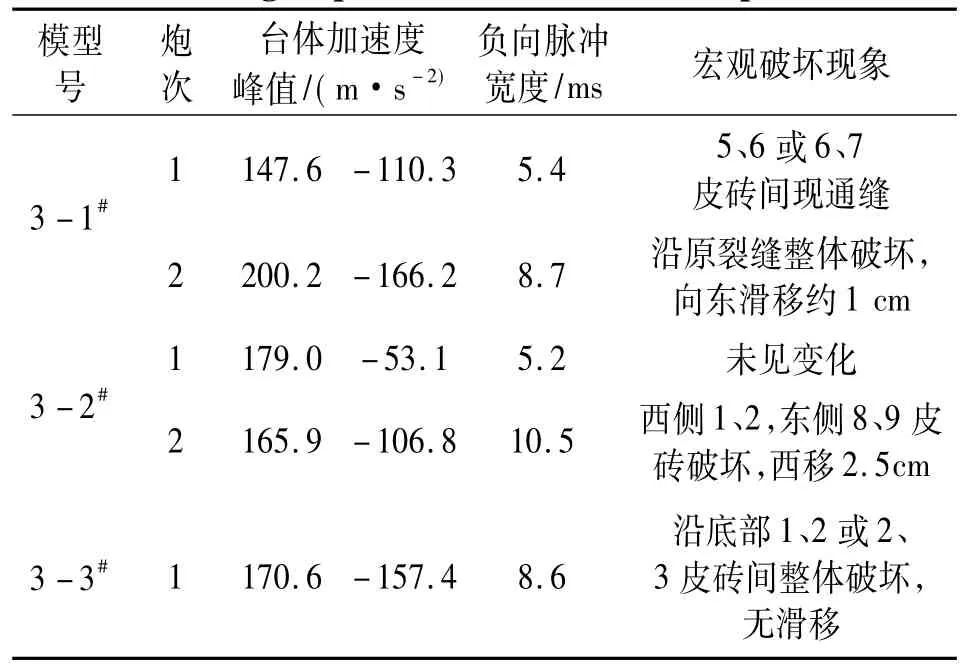
表5 垂直沖擊試驗第3組臺體碰撞加速度參數及宏觀破壞現象Tab.5 Acceleration parameters and macroeconomic failure of the 3rd group in the vertical shock experiment

3 結論

(1)水平向沖擊時模型均表現為水平通縫破壞。該破壞主要因受拉所致而非剪應力引起;模型局部現宏觀破壞后承載能力明顯降低，即使后續施加的加速度與引起破壞時加速度幅值相近或略小，也會致模型破壞嚴重;模型現宏觀局部破壞后若再次受沖擊加速度小于一定數值亦不會致破壞更大。

(2)垂直方向沖擊時模型破壞并非由豎向沖擊作用引起，而由臺體與基座碰撞所致;模型破壞為由碰撞時負向加速度使其受拉導致，即受拉破壞。

(3)砂漿強度4.20～5.97 MPa的磚墻模型承受縱向水平沖擊、加速度主脈沖寬度26.7～41.1 ms時，宏觀開裂或破壞加速度平均峰值為107.65 m/s2;受橫向水平沖擊、加速度主脈沖寬度為48.3～49.8ms時，模型宏觀開裂或破壞時加速度平均峰值為27.0 m/s2;受垂直方向沖擊、主脈沖寬度為5.2～10.5 ms時，模型破壞時垂向加速度峰值約－200 m/s2。

(4)3個獨立沖擊方向中，水平橫向沖擊時模型抗震能力最低，垂直向上沖擊時模型抗震能力最高。

［1］杜義欣，劉晶波，伍俊，等.常規爆炸下地下結構的沖擊震動環境［J］.清華大學學報(自然科學版)，2006，46(3): 322－326.

DU Yi－xin，LIU Jing－bo，WU Jun，et al.Blast shock and vibra－tion of underground structures with conventional weapon［J］.Journal of Tsinghua Univ(Sci＆Tech)，2006，46(3): 322－326.

［2］嚴東晉，唐德高，錢七虎，等.基于VDV隔震標準的爆炸隔震系統研究［J］.振動與沖擊，2000，19(3):77－80.

YAN Dong－jin，TANG De－gao，QIAN Qi－hu，et al.Study on isolation system for blast shock and vibration based on VDV criterion［J］.Journal of Vibration and Shock，2000，19(3): 77－80.

［3］陳妙峰，周早生，唐德高.爆炸沖擊下儀器拋離問題研究［J］.振動與沖擊，2004，23(2):108－110.

CHENMiao－feng，ZHOUZao－sheng，TANGDe－gao. Research on the instrument kick_off under blast shock［J］. Journal of Vibration and Shock，2004，23(2):108－110.

［4］雷真，周德源，張暉，等.玄武巖纖維加固震損砌體結構振動臺試驗研究［J］.振動與沖擊，2013，32(15):130－137.

LEI Zhen，ZHOU De－yuan，ZHANG Hui，et al.Shaking tabletestonearthquake－damagedmasonrystructure strengthened with BFRP［J］.Journal of Vibration and Shock，2013，32(15):130－137.

［5］黃華，呂衛東，劉伯權.爆炸荷載作用下粘貼Polymer Sheet膜材砌體墻防護性能研究［J］.振動與沖擊，2013，32(19):131－138.

HUANG Hua，Lü Wei－dong，LIU Bo－quan.Protective performance of masonry walls strengthened with polymer sheet under explosive loading［J］.Journal of Vibration and Shock，2013，32(19):131－138.

［6］田玉濱，李朝，張春巍.爆炸荷載作用下配筋砌體結構的動力響應［J］.爆炸與沖擊，2012，32(6):658－662.

TIAN Yu－bin，LIZhao，ZHANGChun－wei.Dynamic response of reinforced masonry structure under blast load［J］.Explosion and Shock Waves，2012，32(6):658－662.

［7］GB6722－2003，爆破安全規程［S］.

［8］Crandell F J.Ground vibration due to blasting and its effect upon structures［M］.Boston:BostonSocietyofCivil Engineers，1949.

［9］Langefors U，Kihlstrom B，Westerberg H.Ground vibrations in blasting［J］.Water Power，1958，10:335－424.

［10］Dowding C H，Fulthorpe C S，Langan R T.Simultaneous air blast and ground－motion response［J］.Journal of the Structural Division，1982，108(11):2363－2378.

［11］李伯松，賀永勝，韓乃仁，等.模擬爆炸震動的沖擊試驗機簡介［J］.爆炸與沖擊，2002，22(1):79－82.

LI Bo－song，HE Yong－sheng，HAN Nai－ren，et al.Brief introduction of shock testing machine for simulating blast vibration［J］.Explosion and Shock Waves，2002，22(1): 79－82.

［12］黃維平，鄔瑞鋒，張前國.配重不足時的動力試驗模型與原型相似關系問題的探討［J］.地震工程與工程振動，1994，14(4):64－70.

HUANG Wei－ping，WU Rui－feng，ZHANG Qian－guo.Study on the analogy between scale models with less ballast and their prototypes under shaking table test［J］.Earthquake Engineering and Engineering Vibration，1994，14(4):64－70.

Model experiments on blast shock vibration resistance of masonry wall

LI Li－sha，ZHANG Hong－hai，XIE Qing－liang，DU Jian－guo
(The Third Engineer Scientific Research Institute of the Headquarters of the General Staff，Luoyang 471023，China)

In order to investigate the failure pattern and threshold value of masonry wall under blast shock vibration loads，according to the practical situation of masonry wall in engineering，simplified masonry wall models were established.Experiments under the shock loads acting seperately in three directions were carried out on a shock testing machine for simulating the blast.The dynamic responses of the masonry wall models under the action of shock and vibration as well as the peak values and operation time of acceleration at the moment of failure were investigated.The results show that，for the masonry wall with bottom fixed and all－around constraint unconfined under the load of horizontal shock，the failure displays the form of horizontal straight joint damage.The failure is mainly caused by tensile stress instead of shearing stress.The failure threshold value under the shock loads acting seperately in three directions was obtained by analysis on the experimental results.

masonry wall;blast shock vibration;model experiment;failure threshold value

TU362

A

10.13465/j.cnki.jvs.2015.02.036

2013－06－19修改稿收到日期:2014－02－11

李利莎男，碩士，助理研究員，1979年生

張洪海男，副研究員，1968年生

郵箱:zhh_1968@139.com