探究基于數學思想的數學教學
鐘朝勇
在義務教育課程改革以前,中國的數學課程教學主要以“雙基”教學為主,要求學生掌握基礎知識和基本技能,力求做到基礎知識扎實,基本技能熟練。但是不少中國的教育工作者們總愛走極端,斷然認為基礎知識中的概念、定理、命題靠記憶就能完成;基本技能中的證明、運算靠反復演練就足矣。部分教師帶著這樣的錯誤思想進行教學,學生照樣能取得好成績。但這樣一來,學生就會對數學學習失去基本的興趣和信。蘇聯教育學家烏申斯基說過:“沒有絲毫興趣的強制學習,將會扼殺學生探求真理的欲望。”興趣是學生學習數學的不竭動力和激發自主學習意識的前提。學生一旦失去了興趣,思維將會變得遲緩,記憶將會逐漸減退,意志也會消沉。著名主持人崔永元曾講過他的噩夢:他夢見一道數學應用題。題的大意是:有一個水池,里面有一定的水量,池底有兩根水管,一根水管往水池里注水,另一根水管往水池外放水,兩根水管的閥門同時打開,問什么時候水池能夠注滿或什么時候水池的水會被放完?崔永元郁悶了,這到底是要注水還是要放水啊?看完這個例子,我們可能會覺得崔永元在開玩笑。因為大部分人都知道,這是一個很真實的問題。但也從另一個側面反映出人們對數學是持一種恐懼、害怕、膽怯的心態,認為數學題就是用來折磨人的大腦的事物。
在新的課程標準中明確提出了“四基”教學,即在原有的“雙基”教學上增加了基本思想和基本活動經驗兩項。其目的是為了讓教師和學生們明白:學習數學,不僅要掌握好基礎知識和基本技能,更重要的是要在學習數學的過程中,領悟數學的實質--數學思想。東北師范大學校長史寧中教授曾在重慶師范大學60 周年校慶學術報告中提到:“作為一名優秀的老師,首先要知道數學的實質是什么?數學的實質就是數學思想。其次,一個優秀的老師要做到根據數學內容的實質,創設一個學生能夠接受或感悟的情景。”那么,什么是數學思想呢?史寧中教授提到,數學思想并不是通常我們所說的等量代換、數形結合、換元法等等。他將數學思想分為三個部分:1)抽象;2)推理;3)模型。抽象指的是將外部事物引入數學內部的思想,要學好數學就必須有很強的抽象能力;推理指的是推理論證,從而促進數學內部的發展,學好數學同樣要有一定的推理能力;模型是指溝通數學與外部世界的橋梁,學生要善于構建數學模型。但即便是課程改革專家和眾多數學教育家都主張要追求數學的實質,充分發揮數學思想的作用。但在實際的中小學教學中,這樣做的教師卻屈指可數。
本文用一個具體的中學教學案例,分析在數學教學中如何揭示數學實質的問題,并探討基于數學實質的數學教學對學生學好數學的重要影響。
案例分析
目前,在義務教育教科書七年級下冊的課本中,第八章主要學習二元一次方程組。教材將本章內容分為四個部分:二元一次方程組、消元——解二元一次方程組、實際問題與二元一次方程組以及三元一次方程組的解法(選講)。將本章的知識進行這樣的分塊本沒有什么問題,但教師在實際的教學中卻沒有抓住數學的實質。
我們先來看看第一部分,教材首先以一個實例引入:
籃球聯賽中,每場比賽都要分勝負,每隊勝一場得2 分,負一場得1 分。某隊在10 場比賽中得到了16 分,那么這個隊勝負場數分別是多少?
設勝的場數是x,負的場數是y,你能用方程把這些條件表示出來嗎?
由問題得
勝的場數+負的場數=總場數,
勝場積分+負場積分=總積分
用方程
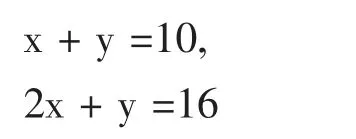
表示。
這種引入二元一次方程和二元一次方程組的思路,主要是想告訴學生二元一次方程和二元一次方程組是如何從現實生活中抽象得出的。這里采用了數學思想---抽象,即將現實生活中的實際情形抽象為數學方程式,使得學生能夠將數學知識和現實生活聯系起來,培養學生的抽象能力。
但教師在教學中,卻沒有注重對學生進行這方面的引導,而把重心放在了讓學生判斷什么是二元一次方程,以及什么是二元一次方程組上。課后作業中也出現大量這種類型的習題,而沒有注重培養學生的抽象思維,幫助學生將知識與實際聯系起來,而這一點,恰恰是這部分教學的重點。
第二部分,消元——解二元一次方程組。這里包含了兩種方法:1)代入消元法;2)加減消元法。教材在這部分的開頭就提到了什么是消元的思想。接著一一介紹了代入消元法和加減消元法,并分別給出了一個純運算的例題和一個應用型例題。在課后的習題中也包括了運算題和應用題。這一部分的數學實質是利用消元的思想求解二元一次方程組。教學目標是兩個:1)讓學生學會利用消元的思想求解二元一次方程組;2)引導學生在簡單的應用題中建立二元一次方程組,并能正確求解。
但有的老師在實際的教學中,卻偏離了正確的軌道,并沒有按照既定的教學目標進行教學。首先,教師會給學生介紹消元的思想;其次,講解代入消元法和加減消元法的具體步驟;最后,粗略地講解一下應用題。接下來的安排,就是給學生布置大量的純運算題。在這些運算題里加入小數、分數、參數等,而應用題在布置的作業里僅占了百分之十左右。
我們從學生角度出發,求解二元一次方程組的方法很簡單,運算過程并不復雜,應該說大部分學生都能夠正確求解。但老師布置大量的純運算題作業,在測試中也給出了大量的純運算題。采用這樣的方式雖然讓學生提高了運算能力,但過多的運算訓練,卻使得學生進入了一個致命的思想誤區:不需要明白如何建立二元一次方程組,也不需要知道二元一次方程組有什么實際意義,更不用管什么是消元思想,只要能夠正確求解出二元一次方程組的解就可以了。有的學校甚至在一周的數學課上,都讓學生練習二元一次方程組的運算,使得學生把解二元一次方程組完全當成了一個“機械性行為”。機械性行為指的是按照指定的法則去對無意義的符號進行機械的操作,既不知道為什么這樣做,也不知道這種操作有任何實際的意義。
帶著這樣的思想誤區進入到第三部分的學習,教師和學生都陷入了兩難的處境。
對于教師而言,他認為學生經歷了一周時間的運算訓練,加之學生以前也做過應用題,所以,在第三部分二元一次方程組的實際應用問題學習中,學生學習起來應該不會有太大的難度。
然而,對于學生而言,恰恰相反。由于在第一、二部分的教學中,老師過多地強調運算,而不注重抽象思維的培養。學生也在一周的時間里,進行沒完沒了的運算,使得學生早已忽視了數學方程式的實際意義,剩下的只是“機械性行為”。當需要學生采用“自動化行為”,即獨立分析問題中的數學關系,根據等量關系建立方程組時,學生自然而然感到十分困難。上文提到的自動化行為指的是操作者在需要時就能隨時告訴你,他這樣做的理由和目的,他也能隨時根據情景的不同做出必要的調整。
老師覺得易、學生覺得難的情形,歸根結底還是由于教師的教學方法和教學理念有問題。蘇聯教育家蘇霍姆林斯基說過:“只有能夠激發學生進行自我教育的教育,才是真正的教育”。同樣,只有適應學生的教學,才是好的教學。在實際的教學中,教師沒有緊緊抓住數學的實質開展教學,從而產生了錯誤的引導方向,使學生不知不覺鉆進了思想的誤區,教師也陷入了尷尬的境地。不僅教學效果達不到預期值,還會使得學生越來越看不到數學的價值,感受不到數學無窮的美,對于學好數學也就失去了應有的信心。
如果教師在今后的教學中,能夠準確把握數學的實質,充分融入數學思想,體現數學“源于實踐,源于生活”的理念,相信學生們在教師的正確引導下,既能夠輕松學習到數學知識的精髓,增強學好數學的興趣和自信心,又能夠體會到數學的生活價值,感悟到數學獨有的魅力!
[1]鄭毓信,梁貫成.認知科學建構主義與數學教育[M].上海:上海教育出版社,2002.
[2]中華人民共和國教育部.義務教育數學課程標準[D].北京:人民教育出版社,2011.
[3]課程教材研究所.數學七年級下冊義務教育教科書[M].北京:人民教育出版社,2012.

