多孔連續介質滲透定律及其擴展

王艷華，潘爭偉，張 劼，李玲霞

（安徽新華學院 土木與環境工程學院，安徽 合肥 230088）

對于大多數松散土體和完整的巖體來說（除裂隙化黏土、裂隙發育的黃土外），一般可以概化成多孔連續介質的滲流問題，滲流問題的定量化表述的基礎理論是達西定律.1856年，法國學者亨利.達西（Henry Darcy）結合法國第戎（Dijon）市的噴泉，研究了均勻砂柱中的滲流問題.

對于大多數松散土體和完整的巖體來說（除裂隙發育的黏土和黃土外），一般可以概化為多孔連續介質，滲流問題的定量化表述的基礎理論是達西定律.1856年，法國工程師亨利.達西（Henry Darcy）通過實驗研究了均勻砂土中的滲流問題，總結出滲流運動的一個重要規律.

達西定律的問世在地下水科學領域具有很重要的意義，它標志著地下水研究由定性描述從此步入定量研究的新階段.達西定律由于形式簡單、概念清晰、求解方便，被認為是地下水動力學最重要和最基本的定律[1]，目前大多數地下水流動問題的數值解、解析解和模擬軟件幾乎都是基于“地下水滲流服從線性滲流定律”假定得到的，例如，地下水運動的基本微分方程、裘布依穩定井流模型、以及FEFLOW、MODFLOW等地下水數值模擬軟件[2].雖然后來研究發現隨著滲流流速的增大，地下水運動規律逐漸偏離線性規律，并且近年來國內外學者也越來越關注地下水非達西流動問題[3-4]，但是目前仍然公認的是：砂性土中的地下水滲流，在低雷諾數下，一般認為Re＜（1～10），達西定律仍然是成立的.本文在一維線性的基礎上，將達西定律擴展到二維、三維體系中，分析均質（非均質）各向同性、異性多孔介質三維滲流定律，使其適用于實際各向同性多孔介質中的流動.

1 達西定律及其公式

達西在《第戎市的公共噴泉》一書中這樣描述他的實驗結論“同一特性的砂子，可以認為體積流量與壓差成正比，而與所穿越的砂層厚度度成反比.”達西滲流實驗（圖1）結果表明：單位時間內流過砂柱的水量Q與過水斷面面積A和水頭差（H1-H2）值成正比，與滲流路徑L成反比，這就是著名的達西公式（或稱定律），其表達式為

式中，Q表示通過砂柱的水的流量；A表示過水斷面面積；K為比例系數，常稱為滲透系數；H是測壓管水頭；（H1-H2）為水頭差；表示水力坡度.

將式（1）進行變換，達西定律的另一種表達形式為

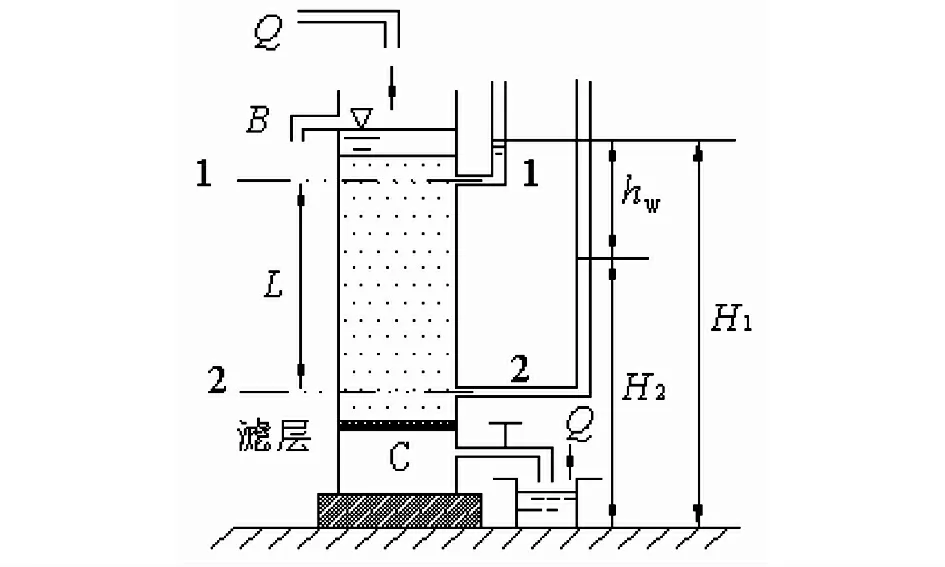
圖1 達西實驗裝置

2 達西定律的適用范圍

（1）從達西實驗裝置可以看出，達西實驗是水在等溫條件下經過均質砂，因此，該實驗適用于均質等溫不可壓縮流體在均質各向同性多孔介質中的一維穩定滲流.

（2）從達西實驗定律可以看出，通過均質砂的滲流速度與其水力梯度呈線性關系，所以，達西定律也稱作線性達西定律.

在流體力學中運用雷諾數Re定義水流流態，在多孔介質滲流中，雷諾數可表達為

式中，d為多孔介質中顆粒的有效粒徑，一般可用d10來代表；v是滲流速度；V是流體的運動黏性系數.

達西實驗定律適用于低雷諾數Re＜（1~10）流體通過多孔介質的層流運動.

（3）在細粒土尤其是黏性土中，由于土顆粒的比表面積大，由于分子力的作用，在土顆粒表面形成強、弱合水，且孔隙小，導致水流在較低水力梯度下難以通過黏性土多孔介質.因此，存在一個起始水力坡度J0，只有當J>J0才能發生流體流動，此時，達西定律可表達為

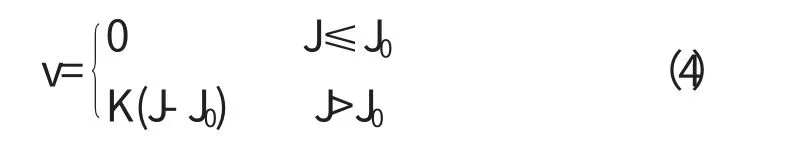
3 達西定律的擴展

達西定律是在一維條件下得到的，而實際介質多是二維各向異性的情況，將達西定律進行擴展，將其擴展到二維、三維條件下各向同性的介質中，使其適用于實際介質的中的流動.

3.1 均質各向同性多孔介質三維滲流定律

當多孔介質為均質各向同性時，K為標量，則三維滲流方程為

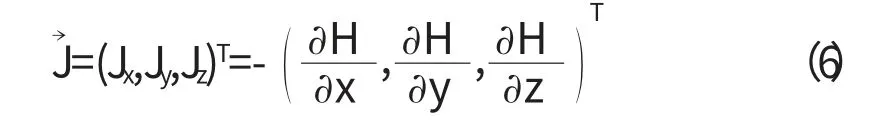
則，達西定律可擴展為

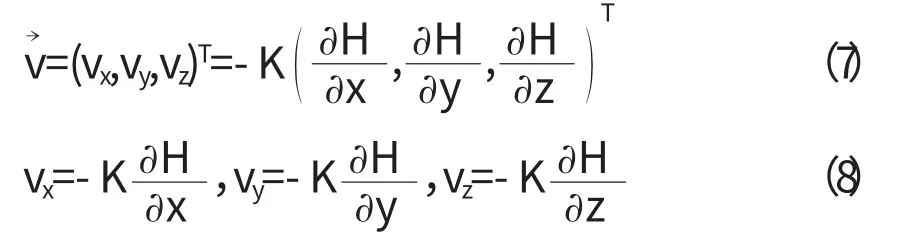
3.2 非均質各向同性多孔介質水平滲流規律

當多孔介質為非均質各向同性時，K=K(x,y,z)，則

以承壓含水層為例，當承壓含水層為層狀多孔介質，且均質水流（ρ,μ 為常數）平行層狀多孔介質層面流動，如圖2所示.

假定Ki,Mi,qi分別表示第i層的滲透系數、厚度和單寬流量.若用達西定理寫出每層的單寬流量，則總單寬流量等于每層單寬流量之和，即

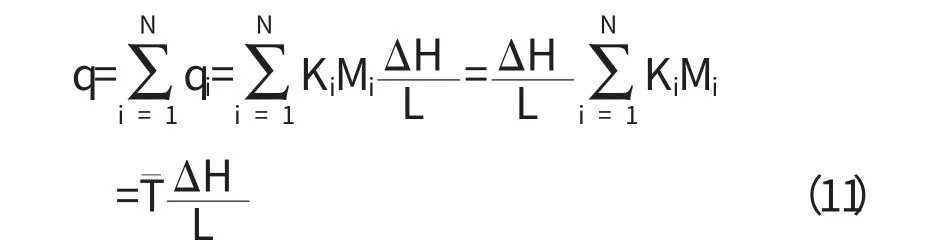
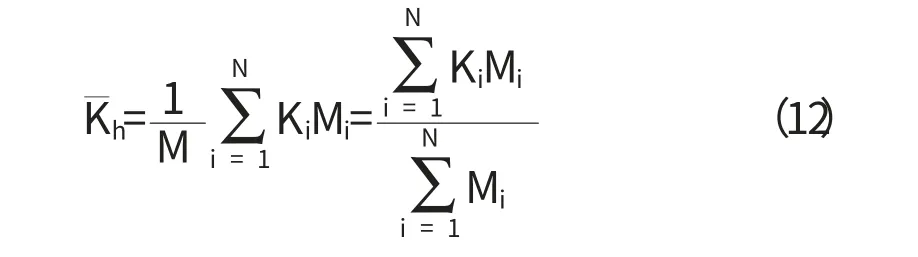
從而可推出，平行多孔介質層面運動的水流透過層狀多孔介質的等效滲透系數可表達為

如果用一種滲透系數沿垂直方向z連續變化（K=k(z)）的含水層替代上述的層狀含水層時，則通過厚度M，且與層面平行流動的含水層中滲流的總單寬流量為（△H/L為常量）

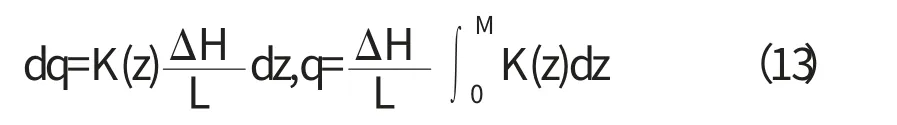
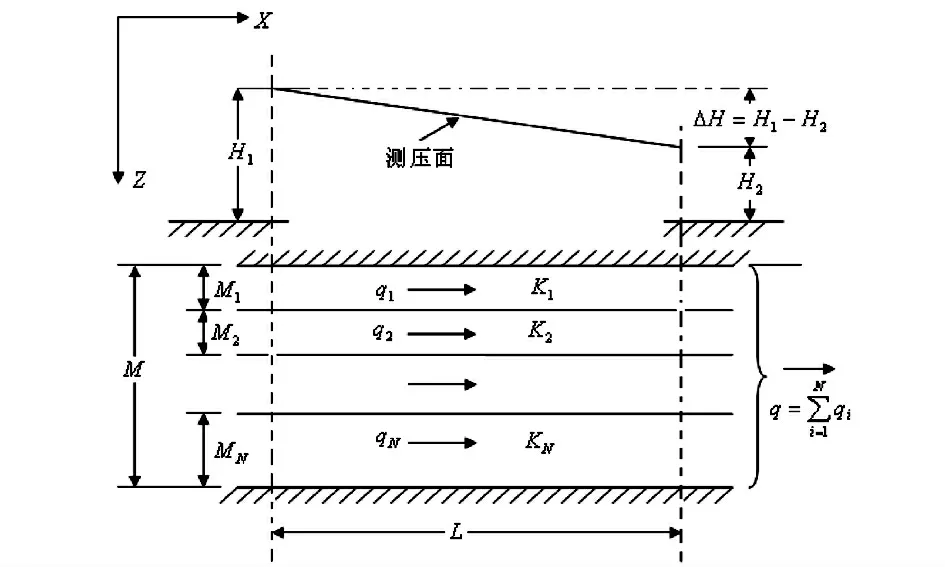
圖2 水流平行層狀多孔介質層面滲流問題

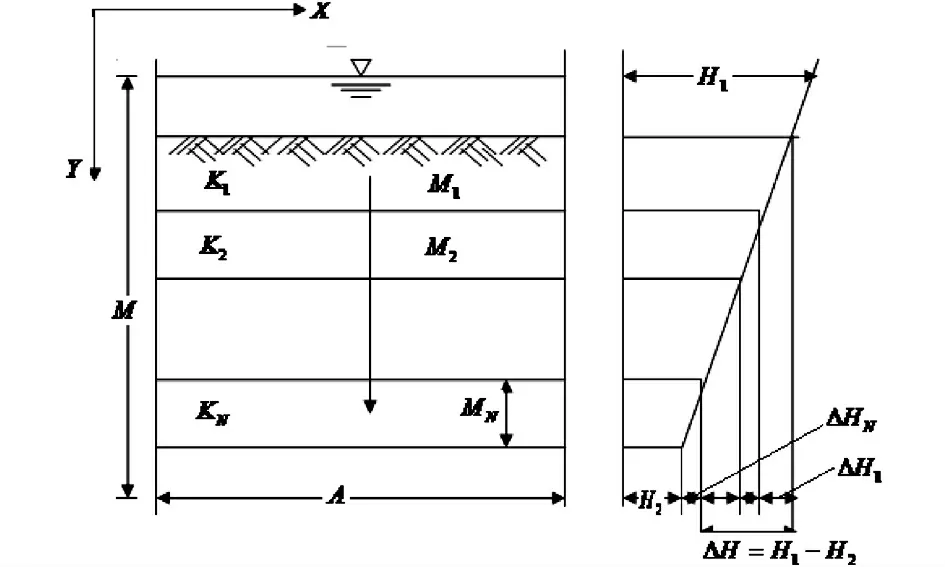
圖3 水流垂直層狀多孔介質層面滲流問題

3.2 非均質各向同性多孔介質垂直滲流規律

當承壓含水層為層狀多孔介質，且均質水流（ρ,μ 為常數）垂直層狀多孔介質層面流動，如圖（3）所示.此時，通過多孔介質的流量為常數，流動路徑與含水層厚度一致是變量，每一層的水頭差是變量，總水頭差△H應等于每層△Hi之和，即

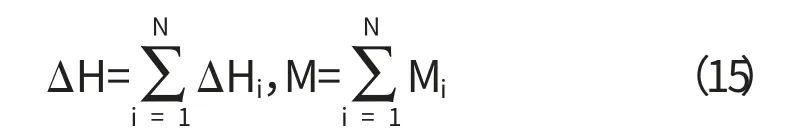
由達西定律得

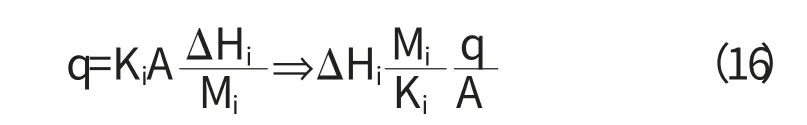
所以

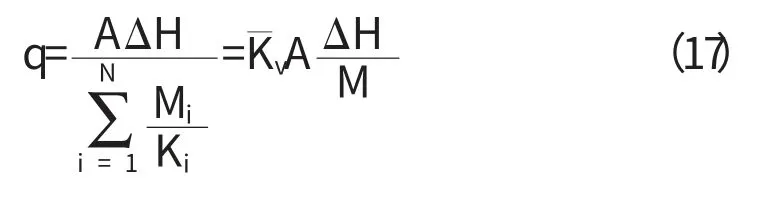
式中，Kv為垂直多孔介質層面運動的水流透過層狀多孔介質的等效滲透系數.

從而得到下列關系式

如果式（18）有一個Ki=0，即存在一個不透水層，那么總的Kv=0，也就是整個層狀多孔介質為不透水層.這一思想用在防水、隔音、隔熱、絕緣、不透氣多層狀復合材料制備時，只要將其中某一層做成隔水、隔聲、不透氣層，就可以達到整體防水、隔聲、隔熱、絕緣、不透氣效果.

如果我們用一種滲透系數沿Z方向連續變化K=k(z)）的含水層替代上述的層狀含水層時，則通過寬度A，流量為q，則水頭差的微小變量為

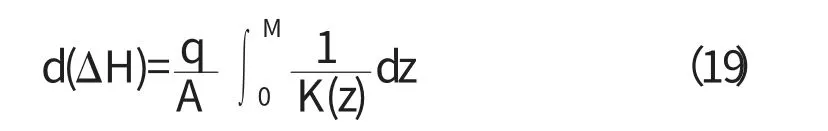
4 結論

達西定律是研究地下水滲流規律的基本理論，在一般運用中具有足夠的精度，但要注意達西公式適用的范圍，將一維線性達西定律擴展到二維、三維體系中，有助于更好的理解達西定律的內涵，同時分析均質（非均質）各向同性多孔介質三維滲流定律，使其適用于實際各向同性多孔介質中的流動.

〔1〕陳崇希，林敏.地下水動力學[M].武漢：中國地質大學出版社，1999.3-12.

〔2〕 高 慧 琴， 楊 明 明， 黑 亮.MODFLOW 和FEFLOW 在國內地下水數值模擬中的應用[J].地下水，2012,34（4）：13-15.

〔3〕萬軍偉，黃琨，陳崇希.達西定律成立嗎[J].中國地質大學學報，2013，38（6）：1327-1330.

〔4〕秦峰，王媛.非達西滲流研究進展[J].三峽大學學報（自然科學版），2009，31（003）：25-29.

〔5〕仵彥卿.巖土水力學[M].北京：科學出版社,2009.