基于極值點概率密度和聽覺模型的瞬態信號提取方法研究

李允公，張金萍，戴 麗

（1.東北大學機械工程與自動化學院，沈陽 110189；2.沈陽化工大學機械工程學院，沈陽 110004）

基于極值點概率密度和聽覺模型的瞬態信號提取方法研究

李允公1，張金萍2，戴 麗1

（1.東北大學機械工程與自動化學院，沈陽 110189；2.沈陽化工大學機械工程學院，沈陽 110004）

零件間的碰撞會誘發瞬態振動信號成分，所以發現和提取瞬態信號有助于設備故障的識別。人類聽覺系統對于突發聲音具有本能的敏感性，因此，基于聽覺系統的運行機制提出了一種瞬態信號提取方法。提出了信號極值點幅值概率密度曲線中存在小幅值局部波動這一含瞬態成分信號的重要特征，并結合頻帶連續性和起始同步性做為瞬態信號提取的線索。基于三種線索，首先對信號進行Gammatone帶通濾波、相位調整和極值點提取，繼而計算各濾波信號極值點的幅值概率密度，并判斷各濾波信號中是否存在瞬態成分，根據判斷結果提取可能與瞬態成分有關的極值點，但因背景信號和干擾噪聲的影響，所提取到的極值點會有一部分與瞬態成分無關，因此，將無關點分為四類并設計了相應的篩選方法。最終，利用篩選后所得極值點生成瞬態信號。數值仿真和實測數據驗證的結果表明，所提方法對于瞬態信號提取具有良好的性能，且在干擾噪聲和背景信號較強時也可實現較好的提取效果。

聽覺模型；聽覺注意；瞬態信號；時頻分解；概率密度

瞬態信號［1－3］是一種常見的振動信號類型，多由設備的短時動力行為所致，尤以零件間的碰撞沖擊為主要誘因，因此，在信號中發現并提取瞬態信號成分對于設備的狀態識別和故障診斷具有較強的實際意義。目前，在瞬態信號提取方面，已有眾多學者進行了深入研究，并提出了多種方法。總體上，已有方法均使用某種特征信息做為瞬態信號識別和提取的依據，如較早時候Angrisani等［4－5］提出一種基于小波局部極大模的方法，并在超聲信號檢測中獲得成功應用；Zhu等［6］提出一種基于K-S檢驗的方法，該方法在齒輪和滾動軸承故障檢測中表現出良好的性能；另外，近年來基于譜峭度［7］的方法受到了廣泛關注和深入研究［8－10］，其主要思路是使用對瞬態沖擊敏感的譜峭度來發現瞬態成分所處頻段，進而確定帶通濾波中心頻率和帶寬，這類方法在瞬態信號提取方面同樣獲得了良好效果。

同時，人類聽覺系統對于突發的瞬態聲信號具有本能的反應［11］，能夠將注意力自動轉移至瞬態聲源，因此，可以考慮基于聽覺系統的基本原理研究瞬態信號的識別和提取方法。而之所以瞬態聲信號會吸引聽覺系統的注意力，主要原因是其具有很強的新異性，即某些特征與先前聲信號明顯不同，并會在相應頻帶上產生幅值突變，從而使聽覺系統自下而上（由耳蝸至聽覺中樞）的調整工作方式［12］，以將注意力聚焦于瞬態信號。進一步的，由于瞬態信號的短時性，則在一段較長時間內，瞬態信號是一個小概率事件，所以，可以考慮基于概率密度函數對瞬態信號成分進行識別和提取。

基于上述分析，并考慮到聽覺模型已在語音［13－14］和振動信號分析［15－16］中表現出良好性能，本文以聽覺系統運行機制為基礎，提出了一種基于極值點概率密度小幅值局部波動特征的瞬態信號識別和提取方法，數值仿真和實驗分析結果表明所提方法能夠有效的提取信號中的瞬態成分，對于間歇式瞬態信號，提取得到的間隔時間具有較好的精度。

1 瞬態信號提取的三種線索

當給定目標信號類型時，無論是現有信號分析理論還是人類聽覺系統，都依據目標信號的某些基本特點進行信號提取，可以稱這些特點為信號提取的線索。對于瞬態信號，可以從多個角度給出提取線索，本文以如下三個特征做為線索。

（1）極值點幅值概率密度的小幅值局部波動

由于信號中的瞬態成分往往會使信號的方差較大，因此，無論信號屬于哪種分布類型，信號的概率密度曲線p（x）中都會存在明顯的長拖尾［17］，示意圖見圖1。

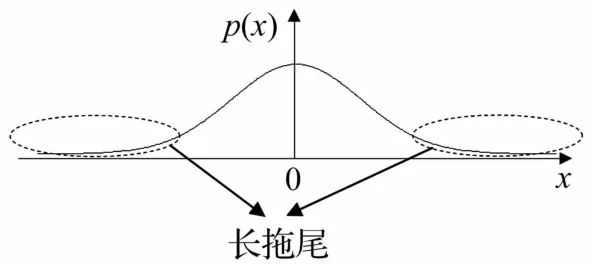
圖1 瞬態信號所致概率密度曲線的長拖尾現象Fig.1 Heavy-tailed in probability density curve induced by transient signal

然而，僅依據拖尾部分無法判斷瞬態成分的幅值范圍。若首先提取信號的所有正極值點，繼而計算極值點幅值的概率密度，則瞬態成分的幅值范圍便會較為清晰，見圖2。由圖2可知，由于背景信號的極值點幅值往往波動不大，加之背景信號幅值與瞬態成分幅值間存在較大差距，概率密度曲線的起始部分會由最大值處快速下降，之后會在瞬態成分幅值范圍內出現若干個小幅波動，這可做為判斷瞬態成分存在與否的重要標志。由圖2（b）可知，從第一個小幅值波動對應的極值點幅值開始，之后的極值點幅值便均與瞬態成分有關。

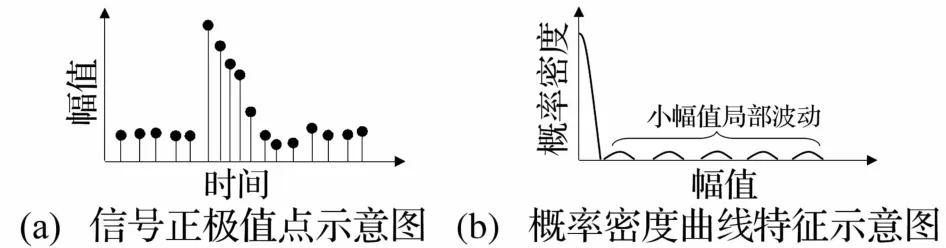
圖2 含有瞬態成分時信號正極值點幅值概率密度曲線特征Fig.2 Feature of probability density curve of amplitude of extreme point of signal with transient component

（2）頻帶連續性

通常情況下，瞬態信號可表達如下形式

式中，γ（t）為平穩信號；a（t）為時域有限衰減函數，其在頻域內的一段低頻連續頻帶內會有明顯幅值。因此，經時頻分解后，瞬態信號會占據一段連續頻帶，并在γ（t）所含頻率處存在峰值。

（3）起始同步性

在時頻域內，瞬態信號在不同頻段內是同時開始波動的，也即具有起始同步性。當然，若時頻分解時不同頻段的相位特性不一致，則會破壞這種同步性，因此，有必要對時頻分解結果進行相位調整。

2 所提方法的實現過程

2.1 方法的基本原理

所提方法的基本實現過程見圖3，首先模擬耳蝸功能對信號進行帶通濾波和極值點選取，為消除帶通濾波時不同頻帶間的相位差異，對濾波結果進行了逆序濾波。繼而計算各頻帶內極值點幅值的概率密度及其導數。基于處理結果，檢驗概率密度曲線中是否存在如圖2（b）所示的小幅值局部波動現象，根據檢驗結果進行極值點選取。進一步的，刪除無關極值點并生成瞬態成分波形。

圖3 所提方法的基本原理Fig.3 Schematic diagram of the proposed method

2.2 帶通濾波與極值點提取

設被分析信號為x（t），時間長度為T。使用聽覺模型研究中常用的Gammatone濾波器組［15，18］對信號進行帶通濾波，設濾波器數目為M，第m個濾波器的表達式為

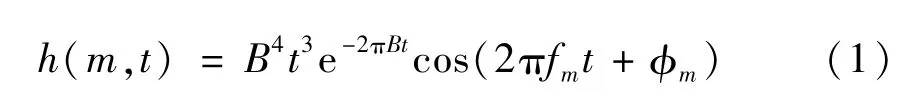
式中，fm為第m個濾波器的中心頻率，相位φm通常取為零，參數B的計算公式為

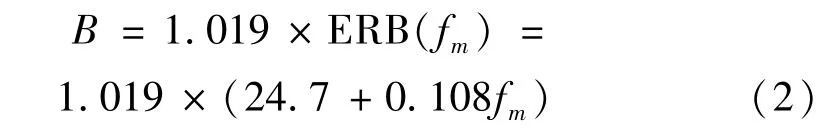
式中，ERB（fm）為濾波器的等價矩形帶寬。

對信號x（t）的帶通濾波為

式中，*表示時域卷積。由于不同fm下的濾波器的相位特性不一致，因此，需對濾波結果進行相位調整。聽覺模型研究中常用逆序濾波［19］方法進行相位調整，這種方法將y（m，t）逆序后重新輸入濾波器，再將濾波輸出反序便可實現相位一致性。但這種處理較為繁瑣，且計算過程的實質與互相關函數是相同的，因此，本文通過計算y（m，t）與h（m，t）的互相關函數實現逆序濾波，即

繼而，只提取y′（m，t）中的正極值點，其他位置均置零，得到y1（m，t）。

2.3 極值點概率密度及其處理

為檢驗各濾波信號中是否存在瞬態成分，首先計算各濾波通道中極值點的幅值概率密度函數p（m，g）

為判斷p（m，g）曲線是否會在峰值之后出現多個小幅值波動，計算p（m，g）關于g的導數

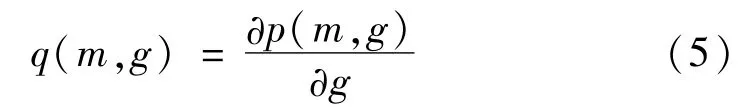
為說明瞬態信號對q（m，g）的影響，生成如圖4所示的仿真信號，該信號為間歇式單頻率瞬態信號與高斯噪聲的混合。不做帶通濾波，直接計算得到的信號的極值點概率密度曲線p（g）及其導數q（g）如圖5和圖6所示。在圖4（b）中，瞬態成分的第4個波峰的幅值為0.083，在圖5（b）中，p（g）經快速下降后在橫坐標g＝0.087處出現向上的拐點，顯然，g＝0.087也正是圖6（b）所示的q（g）的值由負變正的第一個點。由此可知，含有瞬態成分信號的q（g）曲線的第一個特點是：曲線由最小值處逐漸上升，并一定會穿越零點出現正值，且瞬態成分中絕大多數極值點幅值會大于q（g）第一次向上穿越零點前的點所對應的橫坐標值，設此點為

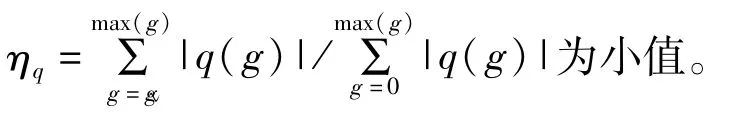
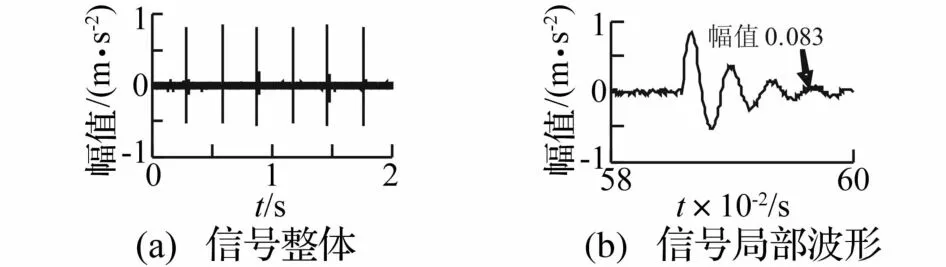
圖4 瞬態信號與高斯噪聲的混合信號Fig.4 Mixed signal of transient and Gaussian noise

圖5 混合信號的概率密度曲線Fig.5 Probability density curve ofmixed signal

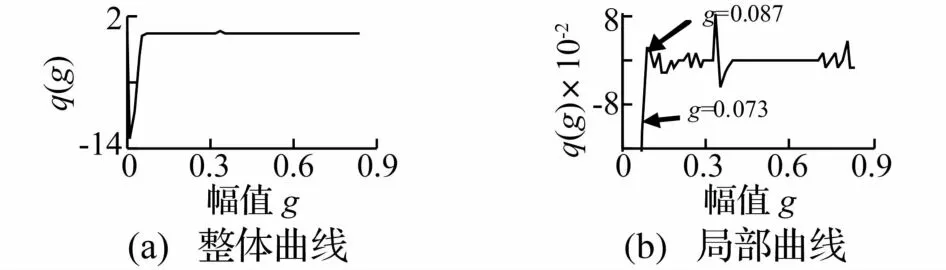
圖6 概率密度曲線的導數Fig.6 Differential of probability density

因此，利用q（m，g），本文設計如下兩條準則判斷第m個通道中是否存在瞬態成分：①在最小值之后，存在向上過零點，設該點橫坐標為~gm；②ηq≤θ1，θ1為給定的閾值，易知，ηq值與瞬態信號和背景信號極值點的點數之比有關，由于瞬態信號中的小幅值極值點不會影響到~gm之后的曲線形狀，因此，考慮到機械振動的普遍特點，本文設θ1＝0.01。可見，準則①是決定性條件，準則②只起輔助作用，且閾值的取值范圍可適當放寬。

2.4 瞬態成分時頻段篩選

利用上述兩條準則，可初步提取與瞬態成分有關的極值點。如果q（m，g）同時滿足兩條準則，則令

否則，令y2（m，t）＝0。

在y2（m，t）中，幅值為1的點所在的位置很可能是瞬態成分極值點出現的位置，但是，由于干擾噪聲和背景信號的影響，會有一部分無關點，需將其刪除。如圖7所示，與瞬態成分無關的極值點可以概括為四類，第一類無關點在時域上呈零星孤立狀態；第二類無關點與瞬態成分無共同頻段，但可能會位于同一時段，在頻率方向上呈零星孤立狀態；第三類無關點在頻域上位于瞬態成分頻段中，在時域上又占據一定的寬度；最后一類無關點位于瞬態成分起始之前的一段時間內，其原因是GT濾波使瞬態信號由單邊衰減變為雙邊衰減。

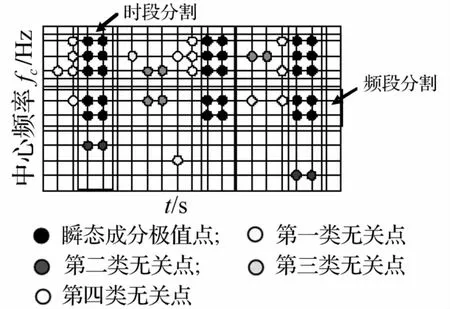
圖7 無關成分極值點與時頻段分割示意圖Fig.7 Irrelevant points and time-frequency segment

2.4.1 第一類無關點刪除方法

由于干擾噪聲和背景信號不會像瞬態成分那樣在一個較高幅值保持一定時間，所以會導致y2（m，t）中出現孤立存在的無關點。為發現此類無關點，首先生成一方波信號ηm（t），令

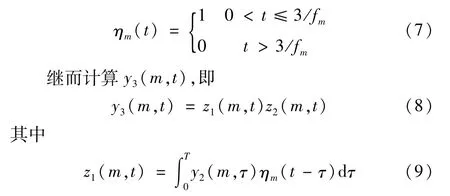
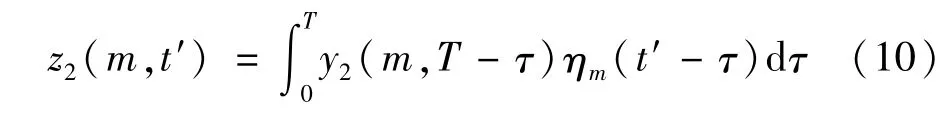
令t＝T－t′，得到最終結果z2（m，t）。可見，z1（m，t）和z2（m，t）相乘可消除卷積運算產生的邊界拓寬現象。y3（m，t）中各點的值反映了卷積運算時ηm（t）每一次移動后所覆蓋的y2（m，t）中幅值為1的點數，所以，搜索y3（m，t）＞0的所有時間段［ti1，ti2］，其中i＝1，2，…，sem，sem為時間段的數目，若某時段內max｛y3（m，t），t∈［ti1，ti2］｝＜3，說明y2（m，t）在［ti1，ti2］內的點為無關點，則令此時間段內y3（m，t）＝0，否則，令y3（m，t）＝1。仍設調整后的y3（m，t）中幅值為1的時間段數目為sem，各時段仍為［ti1，ti2］。

2.4.2 第二類無關點刪除方法（頻段分割）

第二類無關點在頻率方向上呈零星孤立狀態，因此，首先在y3（m，t）中各幅值為1的時間段內提取一個

z2（m，t）則是ηm（t）以時刻T為起點反向移動時與y2（m，t）的卷積，即點得到y4（m，t），即

φ（m）反映了極值點在頻域的分布情況，而無關點在φ（m）中則呈孤立或小幅值狀態，因此，首先刪除φ（m）中的孤立點，設φ（－1）＝0和φ（M+1）＝0，令

經上述操作后，瞬態成分的主要頻率區間即為φ（m）中大于零的區域所對應的頻率區間，從而可對y3（m，t）進行頻段分割，即

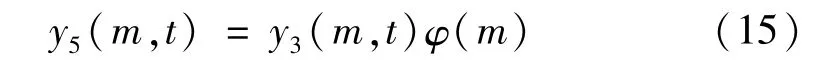
2.4.3 第三類無關點刪除方法

干擾成分和瞬態激勵源的強弱變化會使各瞬態信號極值點的頻域分布狀態不完全相同。但是，無論瞬態激勵源的強度如何，瞬態信號中必然會存在低頻甚至中頻成分，所以，可根據各時段內是否含有φ（m）中的低中頻成分判斷該時段是否與瞬態成分有關。首先生成一函數φ1（m）為

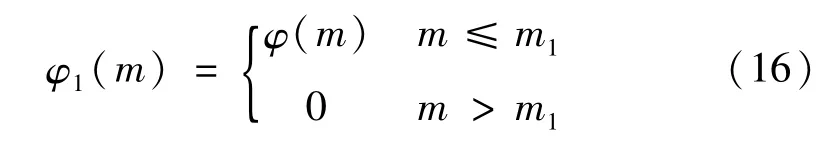
式中，m1的取值應滿足

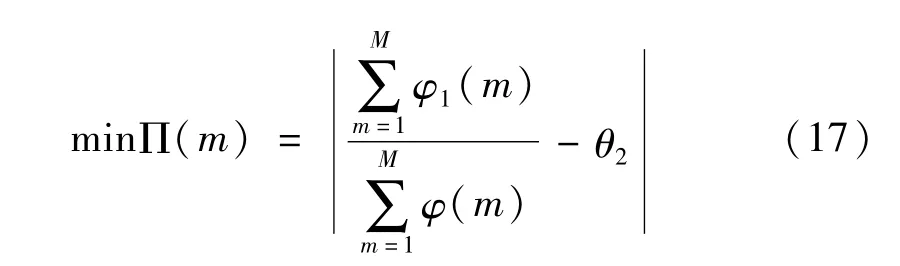
式中，θ2為給定的閾值，本文設為0.5，即φ1（m）只在瞬態信號的一半頻段內與φ（m）相同，其他位置則為零。繼而計算

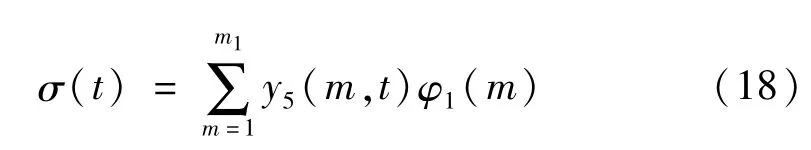
式中：σ（t）已消除了高頻段中的第三類無關點，但是，在中低頻段仍會存在一些無關點需要刪除。

由于y3（m，t）和φ（m）中均將非零幅值設置為1，則σ（t）中與瞬態成分有關的時段內的最大值應與Ω較為接近。因此，在σ（t）中搜索得到各非零時段，設共有U個時段，第u段的時間范圍為［tu1，tu2］，最大值為Ωu＝max｛σ（t），t∈［tu1，tu2］｝，若Ωu＜ζ·Ω，則令該時段內σ（t）＝0，否則令σ（t）＝1，其中ζ為給定的系數，本文取為ζ＝0.6。仍設調整后的非零時間段為U個，第u段的時間范圍為［tu1，tu2］。

經上述操作后，在σ（t）覆蓋的各時段內只存在第四類無關點和瞬態信號，綜合φ（m），將y2（m，t）中的前三類無關點刪除，即

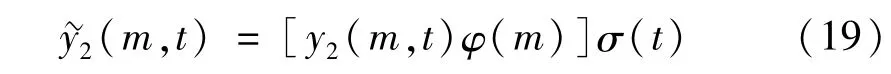
2.4.4 第四類無關點刪除方法（時段分割）

第四類無關點是由濾波運算產生的，如圖8所示，單邊瞬態信號經濾波后將變成雙邊信號，因此，需將圖8（b）中tin之前的極值點刪除，其實質是明確瞬態信號的起始點。

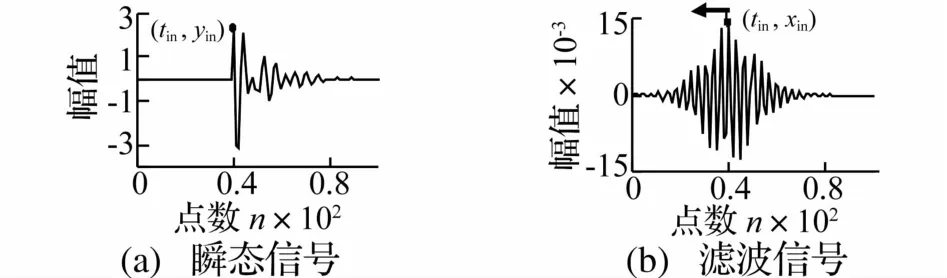
圖8 單邊瞬態信號與雙邊濾波信號Fig.8 single side transient signal and double side filter signal

一方面，在各濾波通道中，瞬態成分與背景信號間通常會存在頻率差異，所以，濾波信號在tin處發生頻率變化的可能性較大。以極值點間時間間隔的倒數表征濾波信號在極值點處的頻率，設（m，t）中第m個濾波通道中的極值點對應的時間為，i＝1，2，…，Im，Im為該通道中的極值點數目，則各極值點處的頻率fp（m，t）設為式中，i＝2，…，Im。

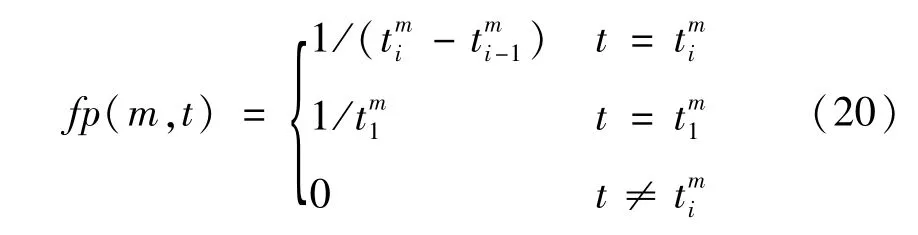
另一方面，不同濾波通道中在小于tin的時間段內所取得的極值點數目會有所差異。但越靠近tin，獲得極值點的可能性會越大，且在tin或其鄰近極值點處則達到最大（是否在tin處達到最大由瞬態信號具體波形決定）。所以，按下式對fp（m，t）和~y2（m，t）進行綜合

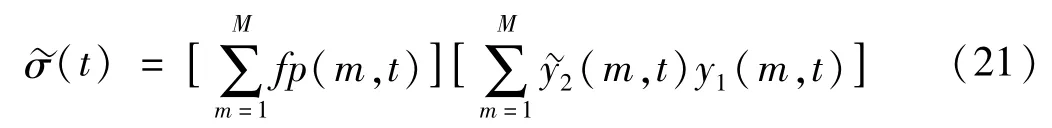
在對應σ（t）中的各非零時段［tu1，tu2］內搜索~σ（t）的分時段最大值，即

同時，由于σ（t）為一系列的方波，為使提取后的瞬態信號的邊界不出現突變，可將σ（t）中的方波替換為半個余弦窗，即對于第u個非零時段，令

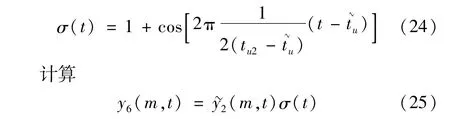
則y6（m，t）中只保留了與瞬態成分有關的極值點。

2.5 瞬態成分生成

利用σ（t）和φ（m）可對信號進行時頻分割，首先生成分割函數，即繼而在y′（m，t）中篩選出瞬態成分的時頻段，即

可將y6（m，t）沿頻率軸相加而得到瞬態波形，但顯然會存在嚴重的幅值誤差。為減小誤差，并考慮到計算簡便性，本文按下式生成瞬態信號波形

式中，ra（m）近似于第m個GT濾波器對瞬態成分中相關分量的幅值增益系數，計算方法為

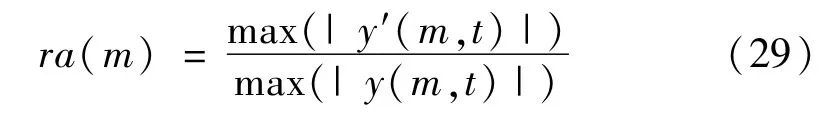
由于GT濾波器間具有較高的重疊度，而且y6（m，t）中幅值較大的濾波通道對生成瞬態成分的貢獻也會較大，因此，令為

式中，“count”為計數，即統計y6（m，t）中對s1（t）影響較大的濾波通道數目，經檢驗，當θ3取為0.02時s1（t）與原始信號的幅值較為接近。

3 方法驗證

經對比測試并根據以往經驗，在以下分析中，GT濾波器數目M取為200（一般情況下，當M＞100時濾波結果不會因濾波器的增加而產生大的變化），中心頻率按對數均勻分布設置。

3.1 仿真信號驗證

3.1.1 驗證1

設仿真信號為

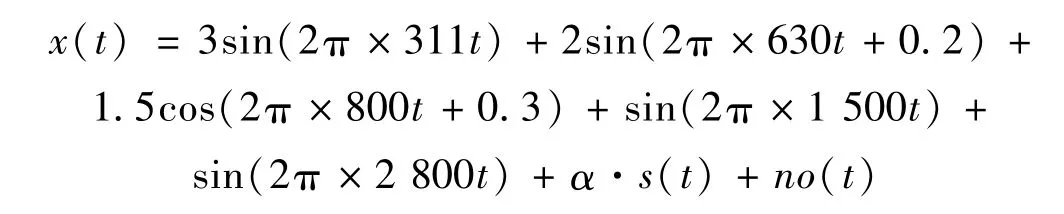
式中，α為瞬態成分增益系數，no（t）為干擾噪聲，s（t）為瞬態成分，表達式為

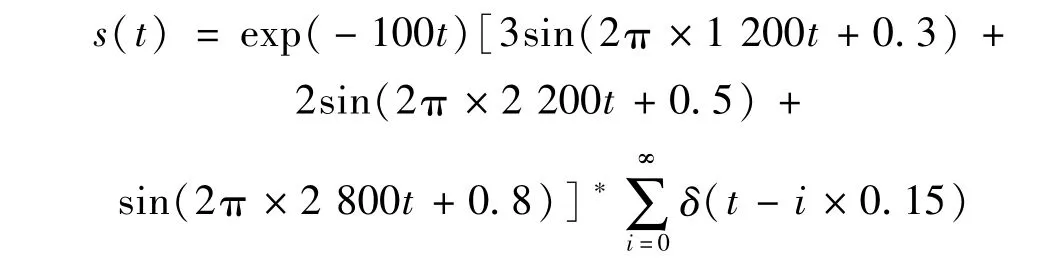
式中，δ（t）為脈沖函數。可見，s（t）中存在若干個以0.15 s為間隔的間歇性瞬態信號，且信號中包括三個主要頻率成分，這兩個特點均與實際的瞬態振動信號相接近。當α＝1、no（t）＝0時，信號x（t）和s（t）的波形如圖9所示，由圖9（a）和圖9（d）可知，在時域波形中很難發現瞬態成分。

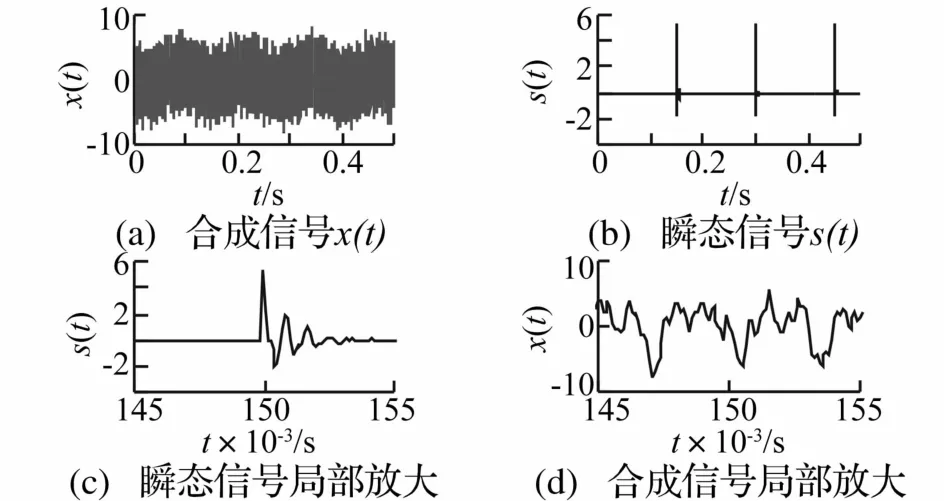
圖9 仿真信號波形Fig.9Waveform of simulation signal

取α＝1，no（t）設為方差為0.01的高斯白噪聲，信噪比為30 dB。使用本文所提方法提取得到的瞬態信號s1（t）及其與s（t）的局部波形對比如圖10所示，幅值譜包絡如圖11所示。由圖10和圖11可見，提取得到的瞬態信號s1（t）與原始信號s（t）間雖然存在幅值差異，但信號波形基本吻合，而且s1（t）能夠表達頻率結構s（t）的頻率結構特征。計算s1（t）和s（t）的互相關系數r（t），r（t）的最大值為rmax＝r（0）＝0.924 4，這也說明提取得到的瞬態信號能夠充分反映原始信號的特點。

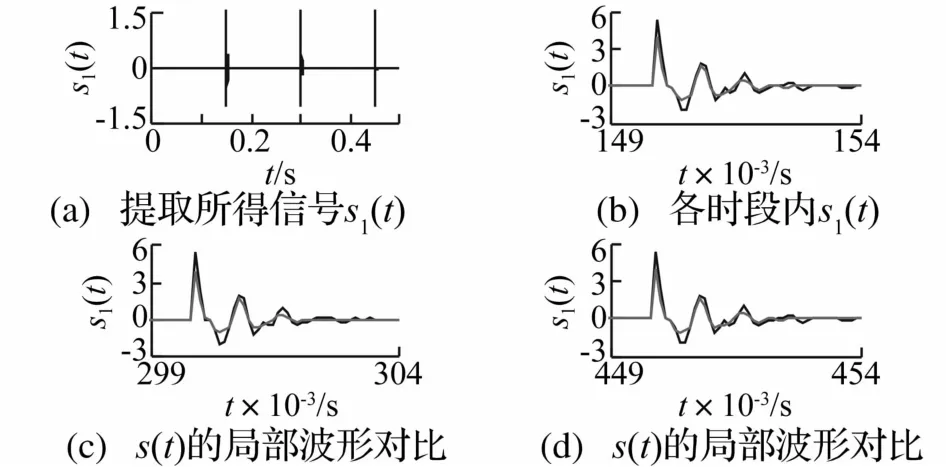
圖10 提取所得瞬態信號及其局部波形對比Fig.10 Transiet signal extracting result and comparison of local waveform

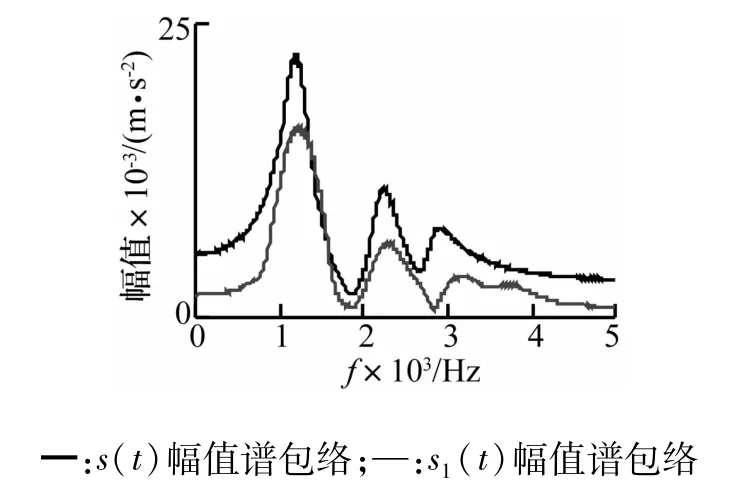
圖11 s1（t）和s（t）幅值譜包絡對比Fig.11 Amplitude spectrums of s1（t）and s（t）

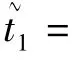
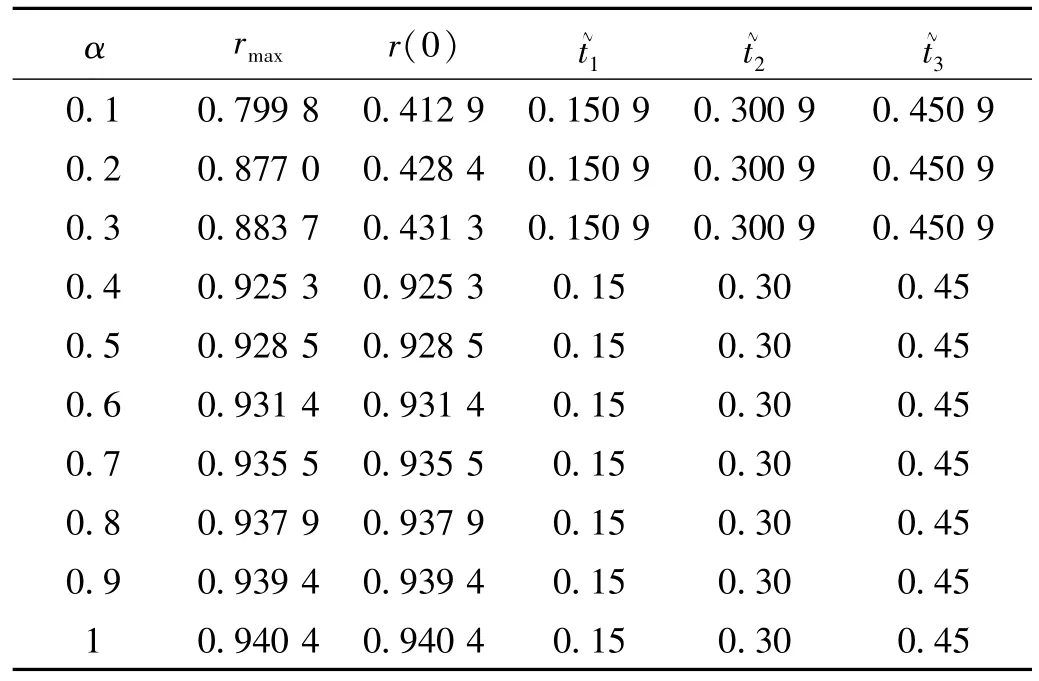
表1 α取不同值時瞬態信號提取效果Tab.1 Extraction effects of transient signal w ith differentα

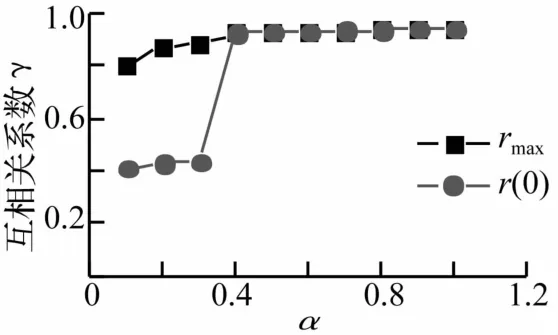
圖12 α取不同值時s1（t）的rmax和r（0）Fig.12 rmaxand r（0）of s1（t）with differentα

為檢驗不同水平干擾噪聲情況下的瞬態信號提取效果，本文以s1（t）與s（t）的互相關系數rmax＝r（0）且rmax＞0.9為限制條件，搜索不同α值時本文方法能夠承受的最大噪聲水平，并以s（t）與no（t）的方差之比var（s）／var（no）（以下簡稱瞬噪比）做為評價指標。當α＝0.4，0.5，…，1.5時，計算得到滿足限制條件的最小瞬噪比如圖13所示，可見，最小瞬噪比基本上在0.01～0.02區間內波動，相當于瞬態信號能量僅為噪聲能量的1%～5%，這說明本文方法具有較強的抗噪聲干擾能力。

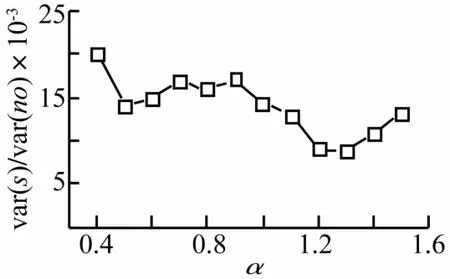
圖13 α取不同值時可實現瞬態信號提取的最小瞬噪比Fig.13 Minmum transient to noise ratio for realizing extraction with differentα

3.1.2 驗證2

為檢驗本文所提方法的抗噪聲干擾能力，將瞬態信號與干擾噪聲混合，仿真信號為

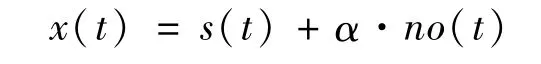
式中，s（t）和no（t）與3.1.1節相同，α為干擾噪聲的增益系數。調整α的值，計算不同瞬噪比時s1（t）與s（t）互相關系數的rmax和r（0），所得結果如圖14所示，由圖可知，當瞬噪比為0.04至0.08時，瞬態信號提取效果很不穩定，主要表現在起始時刻存在較大的誤差；當瞬噪比大于0.08后，rmax和r（0）曲線完全重合，說明起始時刻誤差消失，且隨著瞬噪比的增大，rmax也呈增大趨勢，即提取得到的s1（t）與s（t）越來越相似，尤其是rmax在瞬噪比小于1的情況下便可達到0.96以上，說明本文方法在噪聲能量大于信號能量的情況下也可實現較好的提取效果。

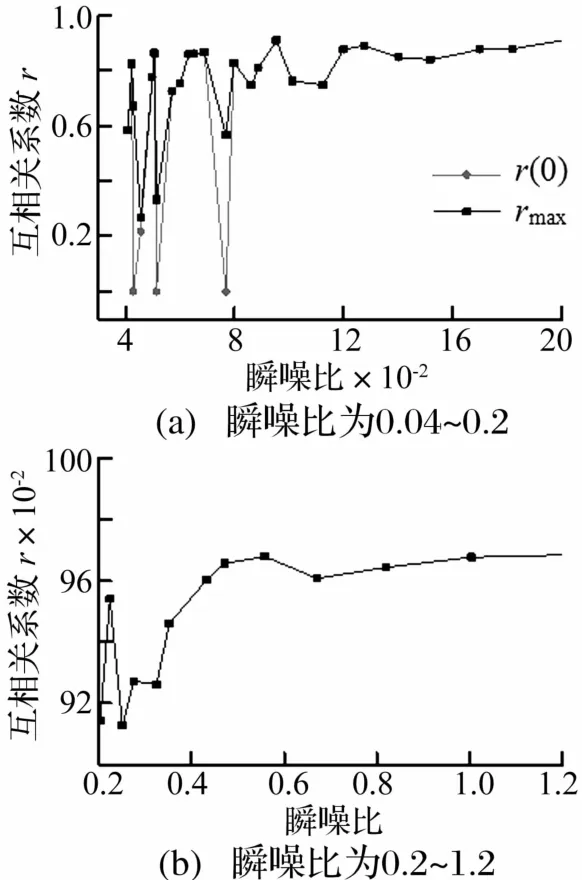
圖14 不同瞬噪比情況下瞬態信號提取效果Fig.14 Transient signal extraction effects under different transient to noise ratio

3.2 實測信號驗證

以某風力發電增速機的實測振動信號為例驗證本文方法，該設備在調試過程中出現間歇式異響現象，測試時的采樣頻率為11 025 Hz，測點所在軸承座支承的齒輪轉速為1 680 r／min。測試得到的一段信號波形如圖15所示，信號經Gammatone帶通濾波并調整相位后的結果y′（m，t）如圖16所示，可見，無論從信號的時域波形還是時頻分布中都很難判斷是否存在瞬態成分。

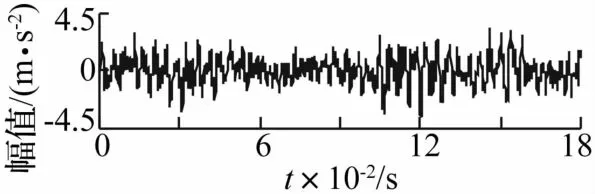
圖15 實測信號波形Fig.15 Measured signa

圖16 信號的時頻分布y′（m，t）Fig.16 Time-frequency distribution y′（m，t）

使用本文方法進行分析，共提取出四個瞬態信號，信號波形如圖17所示，局部波形如圖18所示。圖17中四個瞬態信號的起始時刻分別為0.018 422 s、0.059 676 s、0.099 651 s和0.137 775 s，平均時間間隔為0.039 8 s，所測齒輪旋轉一周所用時間為0.035 7 s，考慮到轉速波動和計算誤差等因素，可以推斷該齒輪每旋轉一周與某零件產生一次碰撞。

圖17 提取所得的瞬態信號Fig.17 Obtained transient signal

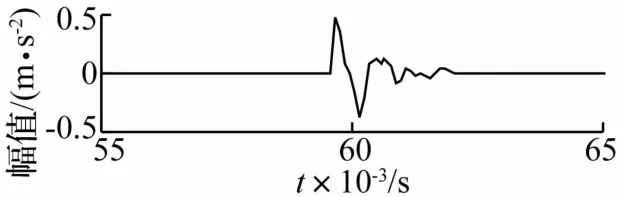
圖18 瞬態信號的局部波形Fig.18 Localwaveform of transient signal

為進步一說明圖17所示信號為所測信號中的瞬態成分，分別計算原始信號和瞬態信號的幅值譜，如圖19所示。可見，圖19（a）中具有共振峰譜型特點的連續譜線部分與圖19（b）所覆蓋的頻率范圍和譜型均較為一致，這也說明本文方法提取到的瞬態信號為由零件碰撞所激發的沖擊響應成分。

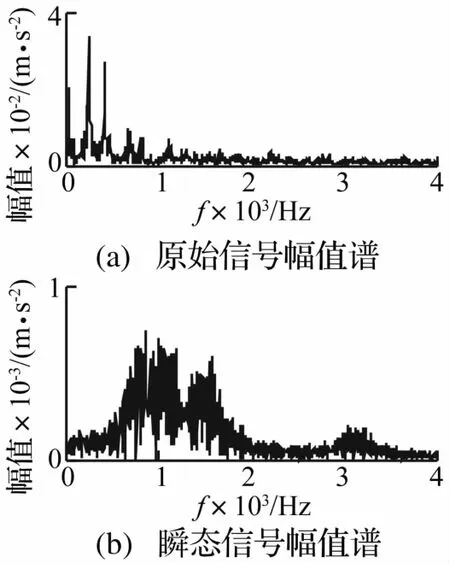
圖19 原始信號和瞬態信號幅值譜Fig.19 Amplitude spectrums of original and transient signal

4 結 論

指出了瞬態成分會使信號極值點幅值概率密度曲線中出現小幅值局部波動這一現象，結合聽覺系統的運行機制，選取了瞬態信號提取的三種線索，并設計了具體的提取方法。數值仿真和實測數據驗證表明，所提方法具有較好的可行性，所提取的瞬態信號起始時間的準確性較高，且當背景信號或干擾噪聲較強時也可獲得較好效果。另外，本文所提方法可以自適應的確定各濾波通道中瞬態信號極值點的幅值范圍，無需人為設定閾值參數。同時，本文研究表明：

（1）利用信號在各頻段分量的極值點概率密度函數可以表征該頻段內是否存在瞬態成分；

（2）起始同步性和頻帶連續性可以作為瞬態信號提取的重要特征信息；

（3）本文模擬聽覺系統的基本原理，基于各頻段信號的極值點實現瞬態信號提取，這說明信號的極值點蘊含了豐富的信息，對于特征提取和目標信號分量檢測都具有較強的實際意義。

［1］Jena D P，Sahoo S，Panigrahi SN.Gear fault diagnosis using active noise cancellation and adaptive wavelet transform［J］.Measurement，2014，47：356－372.

［2］Tse PW，Wang D.The design of a new sparsogram for fast bearing faultdiagnosis：Part 1 of the two related manuscripts that havea joint title as“Two automatic vibration-based fault diagnosticmethods using the novel sparsitymeasurement-Parts 1 and 2”［J］.Mechanical Systems and Signal Processing，2013，40（2）：499－519.

［3］Rafiee J，Rafiee M A，Tse P W.Application of mother wavelet functions for automatic gear and bearing fault diagnosis［J］.Expert Systems with Applications，2010，37 （6）：4568－4579.

［4］Angrisani L，Daponte P，D'Apuzzo M.A method for the automatic detection and measurement of transients.Part I：themeasurementmethod［J］.Measurement，1999，25（1）：19－30.

［5］Angrisani L，Daponte P，D'Apuzzo M.A method for the automatic detection and measurement of transients.Part I：applications［J］.Measurement，1999，25（1）：31－40.

［6］Zhu Z K，Yan R Q，Luo L H，et al.Detection of signal transients based on wavelet and statistics for machine fault diagnosis［J］.Mechanical Systems and Signal Processing，2009，23（4）：1076－1097.

［7］Guo W，Tse P W，Djordjevich A.Faulty bearing signal recovery from large noise using a hybrid method based on spectral kurtosis and ensemble empiricalmode decomposition ［J］.Measurement，2012，45：1308－1322.

［8］Antoni J.Fast computation of the kurtogram for the detection of transient faults［J］.Mechanical Systems and Signal Processing，2007，21（1）：108－127.

［9］Liu H Y，Huang W G，Wang SB，et al.Adaptive spectral kurtosis filtering based on Morlet wavelet and its application for signal transients detection［J］.Signal Processing，2014，96：118－124.

［10］Sawalhi N，Randall R B，Endo H.The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis［J］.Mechanical Systems and Signal Processing，2007，21（6）：2616－2633.

［11］Kaya EM，ElhilaliM.A temporal saliencymap formodeling auditoryattention［C］／／46th Annual Conference on Information Sciences and Systems.Princeton：IEEE，2012：1 －6.

［12］Duangudom V，Anderson D V.Identifying salient sounds using dual-task experiments［C］／／IEEE Workshop on Applications of Signal Processing to Audio and Acoustics.New York：IEEE，2012：1－4.

［13］Hu K，Wang D L.An unsupervised approach to cochannel speech separation［J］.IEEE Transactions onAudio，Speech，and Language Processing，2013，21（1）：122－131.

［14］Arora V，Behera L.Musical source clustering and identification in polyphonic audio［J］.IEEE／ACM Transactions on Audio，Speech，and Language Processing， 2014，22（6）：1003－1012.

［15］Li Yun-gong，Zhang Jin-ping，Dai Li，et al.Auditory-modelbased feature extraction method for mechanical faults diagnosis［J］.Chinese Journal of Mechanical Engineering，2010，21（3）：391－397.

［16］李允公，張金萍，戴麗，等.基于聽覺神經同步振蕩網絡的時頻結構描述方法研究［J］.機械工程學報，2012，48（5）：55－62.

LI Yun-gong，ZHANG Jin-ping，Dai Li，et al.A novel method for time-frequency structure description based on synchronized oscillatory network of auditory nerve fiber［J］.Journal of Mechanical Engineering，2012，48（5）：55－62.

［17］Yu G，Li C N，Zhang J F.A new statisticalmodeling and detection method for rolling element bearing faults based on alpha-stable distribution［J］.Mechanical Systems and Signal Processing，2013，41（1／2）：155－175.

［18］Venkitaraman A，Adiga A，Seelamantula C S.Auditorymotivated Gammatone wavelet transform［J］.Signal Processing，2013，94：608－619.

［19］Slaney M，Naar D，Lyon R F.Auditory model inversion for sound separation［C］／／IEEE International Conference on Acoustics，Speech，and Signal Processing，Adelaide，Australia，April19－22，1994：77－80.

A method extracting transient signals based on probability density of extreme points and an auditory model

LIYun-gong1，ZHANG Jin-ping2，DAILi1

（1.School of Mechanical Engineering＆Automation，Northeastern University，Shengyang 110189，China；2.School of Mechanical Engineering，Shenyang University of Chemical Technology，Shenyang 110004，China）

Transient vibration signals are usually induced by impacts betweenmechanical parts.So，it is important to find and extract transient signals for recognition ofmechanical faults.Considering that the human auditory system is instinctively sensitive to a burst of sound，amethod of transient signal extraction based on the operation mechanism of an auditory system was proposed.An important featurewas found that there are some fluctuationswith small amplitude in the probability density curve of the amplitude of a signal extreme point，if the signal contains transient components.Then，this feature，the continuity of frequency band and its onset synchronism were taken as the cues for extracting transient signals.Based on these three cues，the band-pass filteringwith Gammatone filters，phase adjustment and extreme points extraction for signalswere implemented at first.Based on the extreme points，their amplitude probability densitieswere calculated to judge if there exist transient components in filtered signals.According to judgment results，those extreme points thatmight be related to transient componentswere extracted.However，due to the effects of noise and background signals，parts of the extracted extreme points were not related to transient commponents.Therefore，these points were divided into four kinds and the corresponding screeningmethodswere designed.At last，the transient signalswere formed by using the left extreme points after screening.The results of numerical simulation and actual test data showed that the proposedmethod is effective，especially，it can extract transient signalswith stronger noise interferences and background signals.

auditorymodel；auditory attention；transient signal；time-frequency decomposition；probability density

TH17

A

10.13465／j.cnki.jvs.2015.21.007

國家自然科學基金資助項目（51275080）

2014－09－10 修改稿收到日期：2014－11－19

李允公男，博士，副教授，1976年生