基于二次相關加權閾值的滾動軸承聲發射信號小波包降噪算法研究

王之海，伍 星，柳小勤

（昆明理工大學機電工程學院，昆明 650500）

基于二次相關加權閾值的滾動軸承聲發射信號小波包降噪算法研究

王之海，伍 星，柳小勤

（昆明理工大學機電工程學院，昆明 650500）

針對滾動軸承疲勞損傷初期聲發射信號微弱而易湮沒于噪聲中難以有效檢測的問題，提出一種基于二次相關加權閾值的聲發射信號小波包降噪算法。通過計算原始信號各小波包分解成分自相關函數與噪聲自相關函數的互相關系數（二次相關），對“3σ”閾值加權得到小波包分層閾值，實現對聲發射信號的降噪。仿真分析與實測聲發射信號分析表明，該方法能夠有效去除干擾噪聲，凸顯聲發射沖擊信號。

滾動軸承；聲發射；小波包降噪；二次相關

滾動軸承是工業領域中廣泛使用的機械零部件，由其產生的故障約占旋轉機械故障的30%［1］。滾動軸承故障主要源于接觸交變應力導致的疲勞破壞，在此過程中會產生聲發射信號。研究表明，采用聲發射技術可以比振動檢測更早更準確的獲取滾動軸承損傷信息［2－3］。但在實踐中發現，在損傷初期，微弱的有效目標信號被湮沒于噪聲中，嚴重干擾了對滾動軸承早期疲勞進程的有效監測。

目前對于滾動軸承聲發射信號的降噪研究相對較少，李修文等［4］采用形態濾波的方法對滾動軸承聲發射信號進行了降噪研究并取得了較好的降噪效果。但文中實驗采用的聲發射信號為通過電火花加工出的外圈單一突發型故障信號，這與滾動軸承實際運轉中可能出現突發型與連續型并存現象的自然失效信號有一定差異［5］。尤其在損傷初期，微弱的聲發射沖擊信號被噪聲掩蓋，是難以有效檢測的。因此對自然失效聲發射信號的降噪研究并選擇適合于該類型信號的處理方法是更具實際意義的。

聲發射信號是一種非平穩時變信號，小波包方法是一種多分辨率時頻分析方法，對于非平穩時變信號的處理具有一定的優勢。目前小波包去噪方法主要有時頻降噪、閾值降噪、模極大值降噪、小波熵降噪法以及相關降噪法等［6－8］。本文根據聲發射信號中混有的噪聲特點，提出一種基于二次相關加權閾值的滾動軸承聲發射信號小波包降噪算法。通過仿真及實驗表明，該方法去噪效果較好，可有效檢測出滾動軸承的微弱故障。

1 小波包二次相關加權閾值降噪算法

1.1 小波包及其去噪原理

Coifman與Wickerhauser等［9－10］合作提出小波包理論，小波包分解算法基于雙尺度方程，通過一對正交鏡像濾波器組h（k）與g（k）實現。其數學描述可總結如下：

文獻［11］指出，根據小波變換局部極大值理論，有效信號小波系數的模要比噪聲小波系數的模大得多。基于此原理，在各分解系數中設定適當的閾值，經閾值量化并重構信號，即可達到去噪目的。可采用的閾值函數主要有軟閾值函數與硬閾值函數，硬閾值函數易造成重構信號的震蕩并且連續性較差［12］。因此本文采用連續性較好的軟閾值函數進行降噪。

1.2 基于二次相關的閾值選取方法

采用小波包軟閾值去噪的關鍵在于閾值的合理選擇，閾值過高會導致有效信號丟失，過低則不能將干擾信號完全抑制。常用閾值主要有史坦（Stein）無偏閾值、固定閾值、啟發閾值以及極大極小閾值四類［13］，但對于聲發射信號這種具有極強非平穩特征的信號，單純采用上述四類閾值已經難以奏效。由“3σ”準則［14］可知，假設零均值白噪聲標準差為σ，則其幅值落在［－3σ，3σ］的概率為99.74%。文獻［16］將“3σ”準則應用于具有一定非平穩特征的發動機振動信號的降噪，提出基于小波的自相關降噪法，即若分解系數的自相關函數迅速衰減，則取閾值為3σ；若呈周期性特征，則取閾值為0；若其特性介于二者之間，則視其接近噪聲自相關函數特征的程度而對“3σ”閾值做加權處理。但文獻中并未給出該閾值的加權系數的求解方法。針對上述降噪方法中存在的問題，本文采用求解小波包末層各分解系數自相關函數與噪聲自相關函數的互相關系數的方法，來準確評判小波包分解系數接近噪聲自相關特征的程度。

綜上，最終得到的閾值K可表示為：

式中：ρxiyi為第i個小波包系數的二次相關系數，σi為該小波包系數的標準差。

1.3 降噪實現步驟

利用本文算法對滾動軸承聲發射信號降噪的過程如下：

（1）按文獻［15］，根據有用信號的最小頻率確定聲發射信號小波包分解層數。

（2）引入與最末層各小波包分解系數數據長度一致的噪聲成分，該噪聲成分要盡量與聲發射信號中的噪聲一致。對于仿真信號，可引入零均值高斯白噪聲。而對于實測聲發射信號，因滾動軸承全壽命周期初期階段損傷較小，此階段的聲發射信號可視為背景噪聲。故以初期聲發射信號各小波包分解成分作為對應引入的噪聲數據。

（3）對末層各小波包分解系數進行二次相關閾值（式（4））計算，閾值量化后，將各小波包分解系數進行重構，得到最終降噪信號。

2 仿真信號驗證

聲發射信號為一衰減正弦波［5］，為不失一般性，本文取三種幅值與頻率各不相同的衰減正弦信號與一零均值白噪聲混合作為仿真信號進行分析驗證：

式中：y1代表目標聲發射信號，y2代表噪聲，y代表混有噪聲成分的聲發射信號。Ai（i＝1，2，3）、B分別為聲發射信號幅值與噪聲的幅值，αi（i＝1，2，3）為衰減系數（α＞0），t為時間，fi（i＝1，2，3）為聲發射信號頻率，N1為y1采樣長度。本文取A1＝2，A2＝1.5，A3＝0.8，B＝0.1，α1＝8×104，α2＝4×104，α3＝1×104，f1＝4×105Hz，f2＝2×105Hz，f3＝1×105Hz，N1＝8 192，采樣頻率為1×106Hz。

將該仿真信號按本文1.3小節步驟進行降噪處理，采用db4小波，進行3層小波包分解，降噪處理前后對比如圖1所示。

圖1給出了降噪處理前后時域信號及其功率譜圖對比，從圖中可見，噪聲成分得到良好抑制，三個聲發射沖擊成分更為明顯。

本文通過處理前后信噪比（Signal-to-Noise Ratio，SNR）的對比來評判降噪效果，并采用均方誤差（Mean Square Error，MSE）參數來評價降噪處理后的信號與目標信號的吻合程度。

MSE的數學表達式如下：

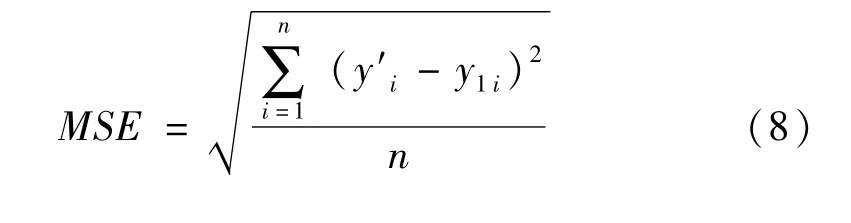
圖1 降噪處理前后效果對比Fig.1 Effect comparison of noise reduction process

式中，y′為降噪后信號幅值，y1為目標信號幅值，i為離散點序號。

SNR的數學表達式如下：

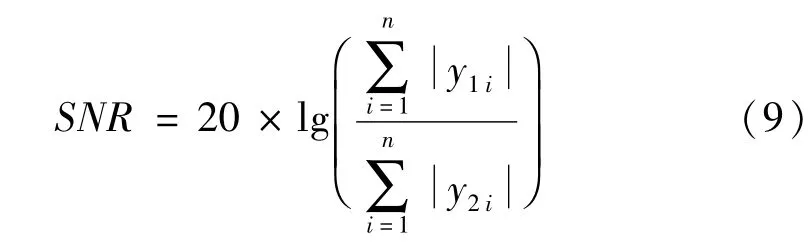
式中，y1為目標信號幅值，y2為噪聲幅值，i為離散點序號。

對仿真信號在不同噪聲水平等級情況下進行了分析測試，分析結果如表1所示。

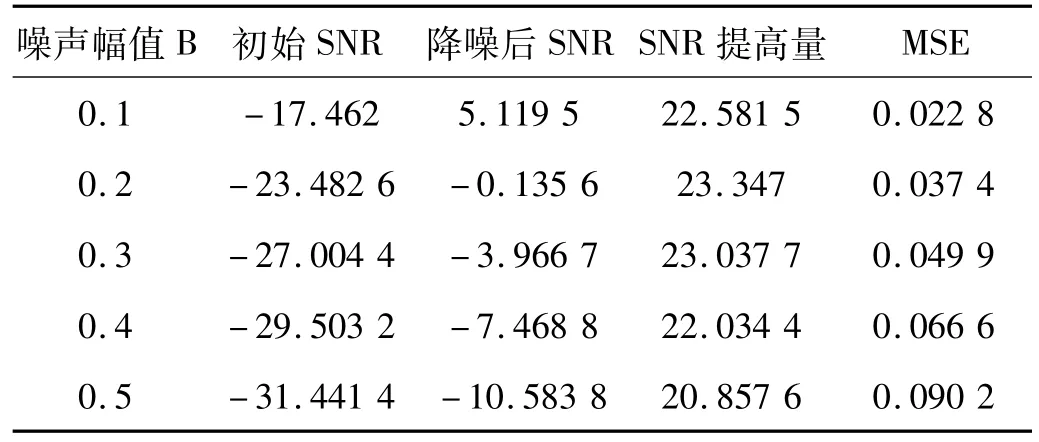
表1 噪聲水平對SNR與MSE的影響Tab.1 The effect on SNR and MSE w ith different noise level

從表1可看出，經過降噪處理后，信噪比提高量均在20 dB以上。降噪后的信號與目標信號的均方誤差保持在較低值范圍內。

3 實驗驗證

本文實驗在自制滾動軸承疲勞試驗臺（見圖2）上進行。該試驗臺由電機、扭矩傳感器、傳動主軸、加載裝置以及待測試軸承組成，測試軸承為推力軸承SKF －51207。為加快疲勞損傷發展速度，將推力軸承的座圈替換為與其直徑一致的45＃鋼圓板，并將聲發射傳感器（型號PAC－R15）粘在其背面進行采集。試驗中轉速保持600 r／min。數據采集設備為PCI－9846H型采集板卡（臺灣，凌華），采樣率為1MHz。本文采用運行第2個小時的數據進行降噪分析，選擇運行初期的聲發射信號作為二次相關系數計算的引入噪聲。

圖2 滾動軸承疲勞試驗臺Fig.2 Fatigue test rig of rolling bearing

按本文1.3節步驟對聲發射信號進行8層小波包二次相關閾值降噪處理，處理前后如圖3所示。由圖3 （a）可見，原始信號存在強噪聲，聲發射沖擊不明顯。圖3（b）、圖3（c）分別為二次相關硬閾值、軟閾值降噪（本文算法）處理后的信號，聲發射沖擊成分均得到明顯增強。

將前文提及的相關降噪法以及四種常用閾值降噪方法進行了比對，均采用軟閾值方法。由圖4及圖5可見，相關降噪法的處理結果相對較好，但時域圖中仍明顯存在一定的干擾噪聲成分。其它四種方法沒有明顯降噪效果。

圖3 二次相關閾值降噪分析Fig.3 Analysis of noise reduction with quadratic correlation threshold

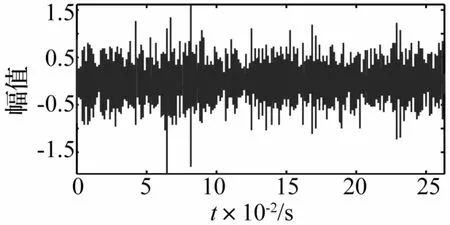
圖4 相關降噪法Fig.4 Noise reduction method of correlation

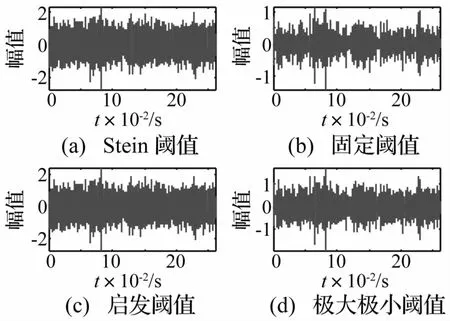
圖5 常用閾值降噪方法處理結果Fig.5 Analysis of noise reduction processwith four common thresholds

該推力軸承的接觸角90°，滾動體數目14，滾動體直徑8mm，節圓直徑48.5mm，經過計算得到滾動軸承座圈的故障頻率［16］為70 Hz。對二次相關硬、軟閾值降噪法處理后的信號分別進行包絡譜分析，如圖6所示。雖然兩種閾值方法得出的包絡譜峰值均位于69 Hz，但硬閾值方法得出的包絡譜中殘留噪聲幅值較軟閾值處理后的大，由此可見采用軟閾值方法更能有效抑制干擾成分。與計算出的座圈故障頻率略有不同的原因可能是由于轉速波動的因素而導致的包絡譜峰值頻率差異。此時將疲勞試驗臺停機，取出軸承座圈觀察，發現座圈部分已經出現點蝕與凹痕。

圖6 降噪信號包絡譜分析Fig.6 Analysis of envelope spectrum of the denoised signal

4 結 論

本文提出基于二次相關加權閾值聲發射信號小波包降噪算法，將小波包分解系數的自相關函數與噪聲的自相關函數的互相關系數作為“3σ”閾值的加權系數，利用得到的加權閾值對聲發射信號進行軟閾值小波包分層降噪。在不同噪聲水平下的仿真分析表明，該方法信噪比提升穩定，失真度小。對實測軸承聲發射信號，該方法能夠凸顯聲發射沖擊成分。降噪后信號的包絡譜峰值頻率與滾動軸承座圈的故障頻率理論值吻合。表明該方法能夠有效抑制噪聲，還原出滾動軸承損傷的有效聲發射信號。

［1］陳進.機械設備故障診斷技術及其應用［M］.上海：上海高教電子音像出版社，2003.

［2］Al-Ghamd A M，Mba D.A comparative experimental study on the use of Acoustic Emission and vibration analysis for bearing defect identification and estimation of defect size［J］.Mechanical Systems and Signal Processing，2006，20（7）：1537－1571.

［3］He D，Li R Y，Bechhoefer E.Split torque type gearbox fault detection using acoustic emission and vibration sensors［C］／／Netwoking，Sensing and Control，April 10－12，2010，Chicage，IL.

［4］李修文，陽建宏，黎敏，等.基于頻域形態濾波的低速滾動軸承聲發射信號降噪新方法［J］.振動與沖擊，2013，32（1）：65－68.

LI Xiu-wen，YANG Jian-hong，LIMin，et al.A new denoisingmethod for acoustic emission signal of rolling bearings with low speed based on morphological filtering in frequency domain［J］.Journal of Vibration and Shock，2013，32（1）：65－68.

［5］李孟源，尚振東，蔡海超，等.聲發射檢測及信號處理［M］.北京：科學出版社，2010.

［6］伍健榮，李雋穎，劉海濤.時頻降噪在圖像序列事件檢測中的應用［J］.吉林大學學報，2012，42（5）：1273－1279.

WU Jian-rong，LI Jun-ying，LIU Hai-tao.Temporalfrequency denoising application in event detection base on image sequences［J］.Journal of Jilin University，2012，42（5）：1273－1279.

［7］隋文濤，張丹.基于峭度的閾值降噪方法及在振動信號分析中應用［J］.振動與沖擊，2013，32（7）：155－158.

SUI Wen-tao，ZHANG Dan.Kurtosis-based threshold denoising method and its application in vibration signal analysis［J］.Journal of Vibration and Shock，2013，32（7）：155－158.

［8］李文，劉霞，段玉波，等.基于小波熵與相關性相結合的小波模極大值地震信號去噪［J］.地震學報，2012，34（6）：841－850.

LIWen，LIU Xia，DUAN Yu-bo，et al.Wavelet modulus maxima denoising of seismic signals based on combined wavelet entropy and correlation［J］.Acta Seismologica Sinica，2012，34（6）：841－850.

［9］Coifman R R，Meyer Y，Quake S.Signal Processing and Compression with wavelet packets［C］／／Proceedings of the Conference on Wavelets，1989：363－379.

［10］趙聯春，馬家駒，劉雪峰.低噪聲軸承異音的小波包分析法［J］.中國機械工程，2004，15（2）：115－118.

ZHAO Lian-chun，MA Jia-ju，LIU Xue-feng.Wavelet packet analysis of abnormal noises of low noise rolling bearings［J］.China Mechanical Engineering，2004，15（2）：115－118.

［11］李寅寅，徐曉蘇，劉錫祥.基于小波包閾值處理的GPS軟件接收機跟蹤結果降噪算法［J］.中國慣性技術學報，2011，19（4）：433－435.

LIYin-yin，XU Xiao-su，LIU Xi-xiang.De-noising method for tracking results of GPS software receiver based on wavelet packet soft-threshold algorithm［J］.Journal of Chinese Inertial Technology，2011，19（4）：433－435.

［12］孟宗，李姍姍.基于小波改進閾值去噪和HHT的滾動軸承故障診斷［J］.振動與沖擊，2013，32（14）：204－208.

MENG Zong，LI Shan-shan.Rolling bearing fault diagnosis based on improved wavelet threshold de-noising method and HHT［J］.Journal of Vibration and Shock，2013，32（14）：204－208.

［13］胡昌華，張軍波，夏軍，等.基于Matlab的系統分析與設計－小波分析［M］.西安：西安電子科技大學出版社，1999.

［14］周品.Matlab概率與數理統計［M］.北京：清華大學出版社，2012.

［15］臧玉萍，張德江，王維正.小波分層閾值降噪法及其在發動機振動信號分析中的應用［J］.振動與沖擊，2009，28（8）：57－60.

ZANG Yu-ping，ZHANG De-jiang，WANG Wei-zheng.Perlevel threshold de-noising method using wavelet and its application in engine vibration analysis［J］.Journal of Vibration and Shock，2009，28（8）：57－60.

［16］Harris T A，Kotzalas M N.Essential concepts of bearing technology［M］.London：Taylor＆Francis Group，2006.

A new noise reduction method for rolling bearing acoustic em ission signals based on wavelet packet transformation w ith quadratic correlation weighted threshold

WANG Zhi-hai，WU Xing，LIU Xiao-qin

（School of Mechanical Engineering，Kunming University of Science and Technology，Kunming 650500，China）

Weak acoustic emission（AE）signals in the early stage of fatigue of rolling bearingsmay be annihilated in noise，and they are difficult to detect effectively.Aiming at this problem，a new method was proposed to reduce noise for these AE signals.The method was based on a quadratic correlation weighted threshold of wavelet packet transformation.The quadratic correlation was defined as the cross correlation coefficients among autocorrelation functions of wavelet packet decomposition components of the original AE signals and the autocorrelation of noise.The threshold for wavelet packetwas obtained by weighting the thresholds of“3σ”with the quadratic correlation coefficients to realize the noise reduction of the AE signals.The analysis of simulated and measured acoustic emission signals showed that this method can effectively remove the interference of noise，and highlight the impulses in acoustic emission signals.

rolling bearing；acoustic emission；wavelet packet noise reduction；quadratic correlation

TG115.28；TH133.33

A

10.13465／j.cnki.jvs.2015.21.030

國家自然科學基金地區基金（51465022，51265018）；云南省自然科學基金（2011FZ017）

2014－12－19 修改稿收到日期：2015－03－16

王之海男，博士生，1983年生

柳小勤男，博士，副教授，1981年生