含不確定性參數的復合材料薄壁結構吸能特性評估方法研究

馮振宇，趙彥強，陳艷芬，解 江

（中國民航大學天津市民用航空器適航與維修重點實驗室，天津 300300）

含不確定性參數的復合材料薄壁結構吸能特性評估方法研究

馮振宇，趙彥強，陳艷芬，解 江

（中國民航大學天津市民用航空器適航與維修重點實驗室，天津 300300）

由于復合材料性能分散度大、加工精度較低，為復合材料薄壁吸能結構引入了不可忽略的不確定性因素，為此，提出了一種含不確定參數的復合材料薄壁結構吸能特性的評估方法并進行了算例研究。復合材料薄壁圓管是一種典型的吸能元件，圓管的壁厚和內徑是對其吸能特性有顯著影響的特征幾何尺寸，考慮了這兩個參數的不確定性，在準靜態壓潰的條件下評估了薄壁圓管的引發比應力和比吸能這兩個關鍵吸能指標。首先，利用區間分布來描述壁厚和內徑的不確定性，其次應用有限元方法建立區間內不確定參數和結構吸能特性指標間的二階響應面函數，最后對響應面函數進行區間攝動從而確定吸能特性指標的分布區間。算例研究結果顯示，與比吸能相比，引發比應力受壁厚和內徑不確定性的影響更大。此外，相比于內徑，壁厚的不確定性對吸能特性影響更顯著，因此為獲得穩定的結構吸能特性應盡量提高復合材料圓管壁厚的加工精度。

復合材料薄壁結構；吸能特性；不確定性；區間模型；有限元分析

復合材料因其高比強度、高比模量等優異性能，在飛機結構中的應用比例越來越大，由于其損傷、破壞和失效模式與金屬結構顯著不同，導致飛機結構的抗墜撞性能隨著復合材料結構成為主承力結構或出現在主傳力路徑上而發生明顯改變［1－2］。因此，復合材料結構在飛機墜撞過程中的吸能特性及其吸能設計近年來受到了國內外工程、學術界的廣泛關注［3－4］。

無論金屬還是復合材料，薄壁結構都是一種典型的吸能結構形式，如薄壁圓管、方管和波紋板等。薄壁結構具有剛度大、穩定性好和吸能效率高的特點。不同的是，復合材料的力學性能比金屬材料的分散性大，復合材料薄壁結構的成型工藝也更復雜，實際工程中由于加工精度的限制和材料性能的分散性導致復合材料薄壁結構的幾何尺寸和物理性能具有不可忽視的不確定性［5］。這些參數的微小變化都會改變結構的力學響應特性和失效破壞模式，從而影響其吸能特性，導致在工程中不得不通過大量實驗來確定復合材料薄壁結構破壞吸能的力學行為。除了試驗方法，針對應用于飛行器和汽車上的復合材料吸能薄壁結構，研究人員近年來也做了大量的仿真分析工作［6－8］。數值仿真主要采用顯式求解結構有限元的數值方法模擬復合材料結構破壞吸能這一瞬態強非線性過程，常用LS-DYNA、MSC-DYTRAN和PAM-CRASH大型商用有限元軟件。但這類研究通常以幾何／材料參數的名義值或平均值建立確定性模型作為研究對象進行分析，忽略材料性能和結構尺寸等參數分散性，計算分析結果與實驗值往往存在較大差異。可見，用常規的確定性的方法已經很難評估和分析這種不確定來源多、分散度大的復合材料結構和非線性力學問題。綜上，在進行復合材料薄壁結構吸能特性分析時引入不確定性理論、建立含不確定參數的復合材料薄壁結構吸能特性的評估方法工程意義顯著。

當前已有學者應用不確定性理論在線性范圍內來研究復合材料結構的力學問題。張麗娟［9］利用區間方法對考慮材料參數不確定性的復合材料層合板屈曲問題進行了研究，苑凱華［10］利用區間方法對考慮幾何參數和材料參數不確定性的復合材料壁板的顫振問題進行了研究。上述研究表明運用區間方法可以有效的建立含不確定參數的復合材料結構模型并預測其可能的力學行為。由于結構碰撞吸能是強非線性瞬態動力學問題，比隱式求解的線性力學問題復雜得多，將不確定理論用來研究結構吸能特性的案例還不多，僅有Salehghaffari對含不確定參數的金屬圓管的吸能特性進行了研究。但對于復合材料薄壁結構其參數分散性更大，工程中受試驗條件和成本的限制樣本空間往往有限，有些參數如結構的特征尺寸等，無法得到精確的分布特征，難以通過文獻［11］中所述方法確定結構的吸能特性。

在工程中通常難以得到復合材料薄壁結構中某些分散度大的重要參數的概率分布，而通常可以確定其取值范圍的上下界。為此提出了基于區間的含不確定參數復合材料薄壁結構的建模方法和其吸能特性的分析方法。首先用區間對不確定參數進行描述，根據區間設計實驗點，然后利用顯式瞬態有限元對確定性參數的復合材料薄壁結構進行吸能特性分析，并采用響應面方法擬合出確定性薄壁結構吸能特性指標與結構參數間的響應面方程，最終通過對響應面方程進行區間分析確定含不確定參數的復合材料結構吸能特性指標的分布區間。并應用該方法對考慮加工公差的復合材料薄壁圓管在壓潰載荷下的吸能特性進行分析，揭示幾何特征尺寸的不確定性對復合材料薄壁圓管吸能特性的影響。

1 不確定參數的區間表示

復合材料薄壁結構的吸能特性與復合材料的彈性模量、剪切模量、密度以及結構的幾何尺寸等參數有關，這些參數可用x1，x2…，xn表示，在確定性結構吸能特性分析中，常使用這些結構參數的確定值或中值xci，而在不確定性結構吸能特性分析中，還需要考慮結構參數不確定性的影響。通常對結構參數的不確定性信息掌握較少而難以確定其概率特性，而確定不確定參數的界限則相對容易，用區間符號可以表示為

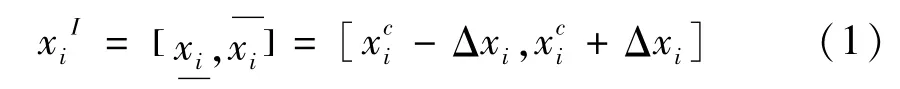
2 構建響應面

2.1 中心組合試驗設計

為建立含不確定參數薄壁結構吸能特性評估模型，需要具備關于結構吸能特性指標與參數之間的函數關系。由于復合材料薄壁結構的破壞吸能機理復雜，無法建立解析的函數關系表達式，但可以根據數值計算結果，采用統計推斷的方法擬合函數方程。本文采用響應面法，擬合參數區間內結構參數與吸能特性指標間的函數關系。

為以較小的計算或試驗成本得到滿足精度的響應面方程，需根據參數區間，通過實驗設計來選擇樣本點。中心組合試驗設計是響應面法研究中常用的實驗設計方法，其試驗點分布見圖1。

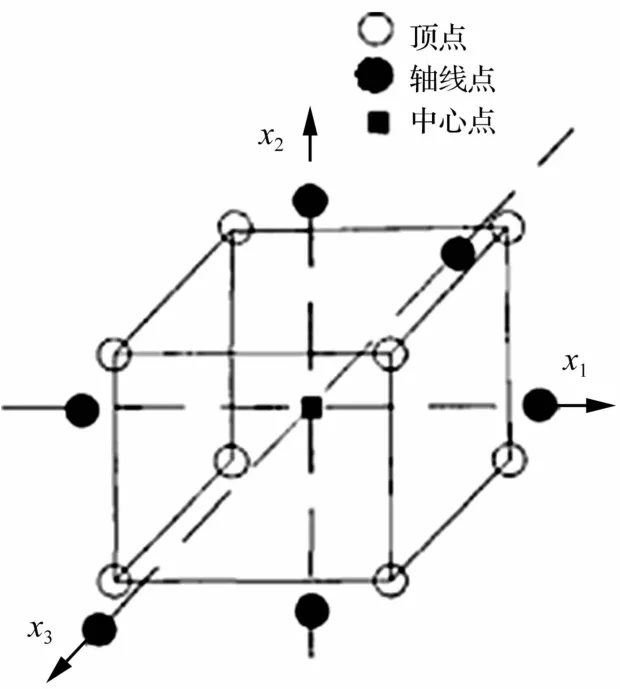
圖1 中心組合設計實驗點分布圖Fig．1 Experimental point distribution of central composite design

對n（n≥2）個因素的中心組合設計需要進行的試驗總數為N＝2n+2n+nc。試驗由三個部分組成：2n個立方體頂點處的試驗、2n個軸點處的試驗及nc次中心點重復試驗。通過中心點處的重復試驗可以提高擬合方程的精度。中心點處重復試驗次數與考察因素的關系見表1。

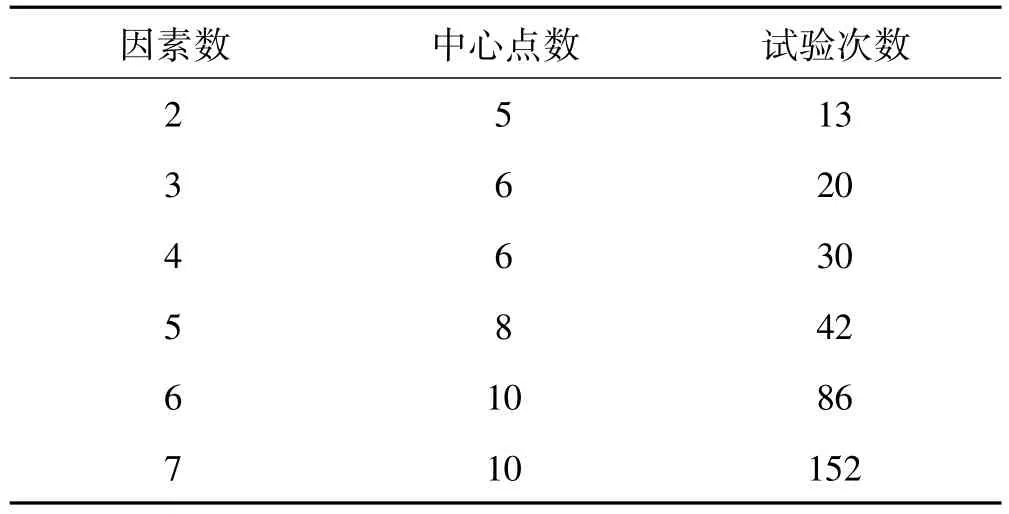
表1 中心組合設計的因素數與試驗次數Tab.1 The number of factors and tests of central composite design

2.2 確定響應面方程

在確定響應面方程時折中精度要求和計算成本，采用二次多項式，并利用最小二乘原理確定多項式系數，得到響應和參數變量之間的函數關系。建立完全二階響應面方程：式中為響應面近似函數；n為模型設計變量的數目；xi為模型設計變量；c0、ci、cii和cij為響應面方程待定系數。

由試驗設計確定的m個樣本點組成設計變量矩陣X，通過確定性分析方法計算樣本點的吸能特性向量Y；計算值與響應面擬合值的誤差組成的向量為ε，各矩陣向量之間的關系

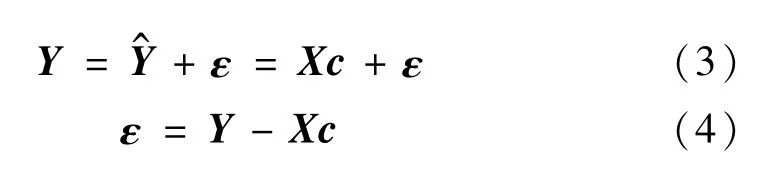
待定多項式系數向量c用最小二乘法擬合求解：

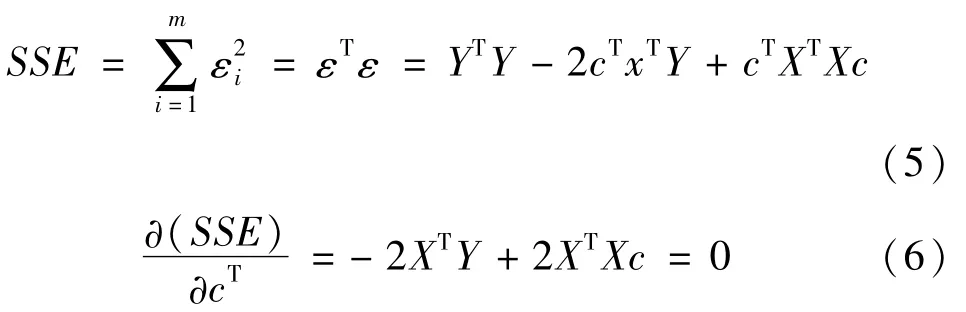
式中；SSE為誤差平方和。系數向量c的估計為：

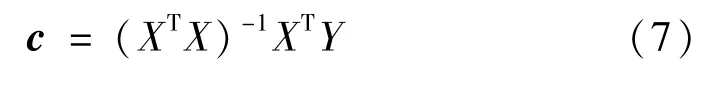
由此得到響應面方程后，為檢驗響應面擬合程度需進行R2檢驗

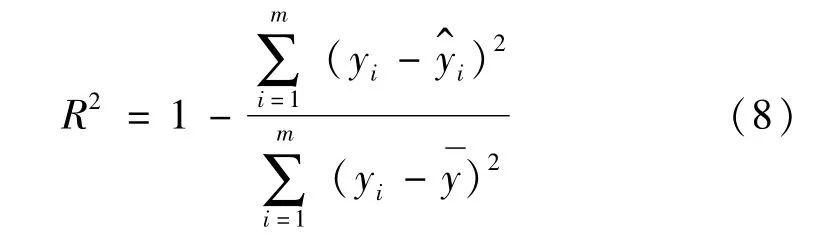
3 吸能特性指標區間的確定

確定在參數區間對應的響應面方程的解區間，就可得到含不確定參數的復合材料結構吸能特性指標的分布區間，采用區間攝動法來確定響應面方程的解區間。

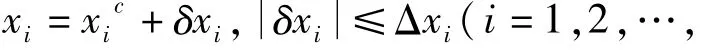
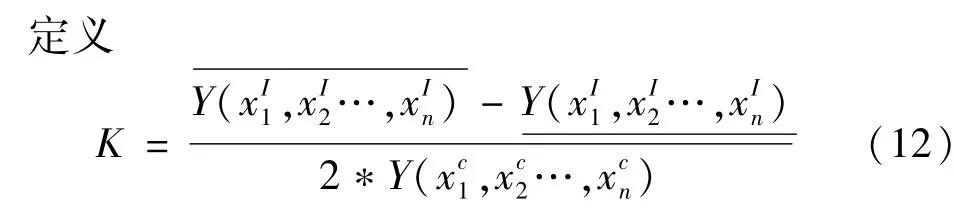
來衡量區間的分散度，K值越大區間越分散。

4 含不確定參數復合材料吸能特性評估流程

評估含不確定參數復合材料吸能特性，首先應對參數進行初步篩選，并確定待考慮參數的分布區間；根據參數的分布區間，利用中心組合設計實驗設計方法安排實驗點；使用LS-DYNA計算實驗點的響應值；根據計算結果確定響應面方程；利用區間分析方法，確定吸能特性的分布區間。圖2給出含不確定參數復合材料薄壁結構建模和其吸能特性評估的流程。

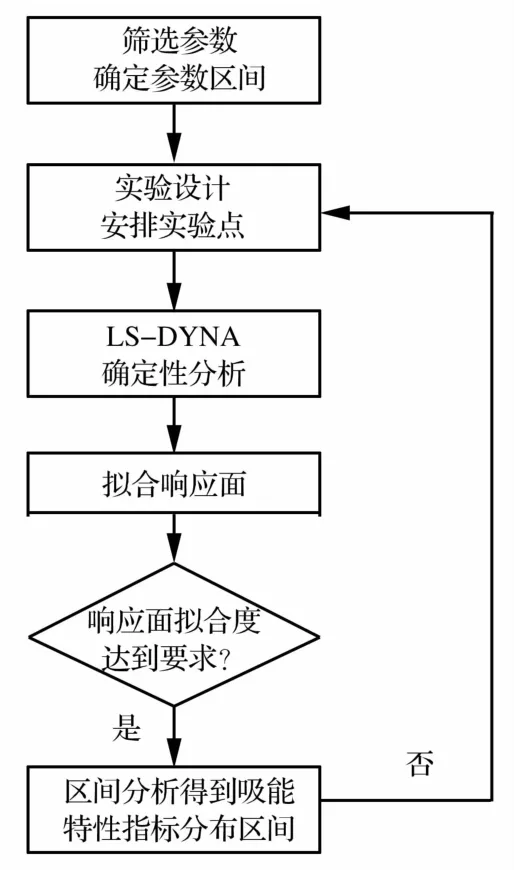
圖2 含不確定參數復合材料吸能特性評估流程圖Fig．2 The flow chart of analyzing energy absorbing characteristics of composite structure with uncertain parameters

5 算 例

5.1 吸能特性指標

采用比吸能、壓潰比應力和引發比應力3個指標來描述結構在準靜態軸向載荷作用下發生壓潰破壞的過程中吸收能量的力學特性。

其中，比吸能（SEA）是結構有效壓潰破壞長度內單位質量（m）所吸收的能量（EA）：

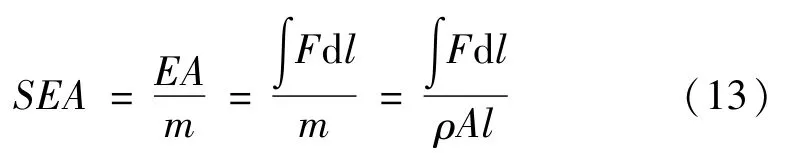
式中：ρ為材料密度，A為薄壁管橫截面積，l為壓潰長度。

壓潰比應力（SCS）作為壓潰載荷的評價指標是由壓潰過程中的瞬時壓潰力（F）除以薄壁管的密度（ρ）及橫截面積（A）得到的：

引發比應力（TSS）是結構被壓潰破壞的門檻值，用于評價結構在外力作用下發生破壞吸能難易程度的指

5.2 參數確定的復合材料圓管吸能特性分析

本文的基準模型為高100 mm，內徑50 mm，壁厚1．84 mm，頂端外側設有45°導角的復合材料薄壁圓管。圓管由14層碳纖維增強環氧樹脂層合而成，其中牌號為T700的碳纖維體積分數為64．3%，薄壁圓管的鋪層方式為［+45／－45／90／0／0／90／0］S，環氧樹脂的牌號為QY8911。標，是比載荷－位移曲線的初始峰值。

在LS-dyna環境中使用Belytschko-Tsay殼單元建立了上述復合材料薄壁圓管的單層等效有限元模型。模型中單元特征長度為2mm，復合材料圓管選取MAT 54材料模型，具體材料參數見表2。圓管上方壓板采用20號剛體材料，圓管底端節點固定約束，頂端為自由端。有限元模型共有4 378個殼單元，4 497個節點。文獻［12］的研究表明使用Ls-dyna進行壓潰仿真時，在加載速度小于40 km／h的條件下，薄壁圓管在不同加載速度下的“載荷－位移”曲線基本相同，并與準靜態試驗結果吻合。模擬仿真中，軸向壓縮的加載速率設置為5 000 mm／s勻速加載，使用8個CPU核心并行計算，耗時369 s。圖4給出了本次仿真與文獻［6］中實驗所得“載荷－位移”曲線的對比圖。表3給出了仿真與實驗所得吸能數據的對比。從圖4和表3中可知仿真所得曲線和實驗曲線較為吻合，引發比應力峰值誤差3．59%，比吸能誤差4．06%，仿真模型可用于接下來的研究工作。

圖3 復合材料薄壁圓管有限元模型Fig．3 The finite elementmodel of the thin-walled composite tube

表2 復合材料薄壁圓管材料參數Tab.2 Material properties of thethin-walled composite tube

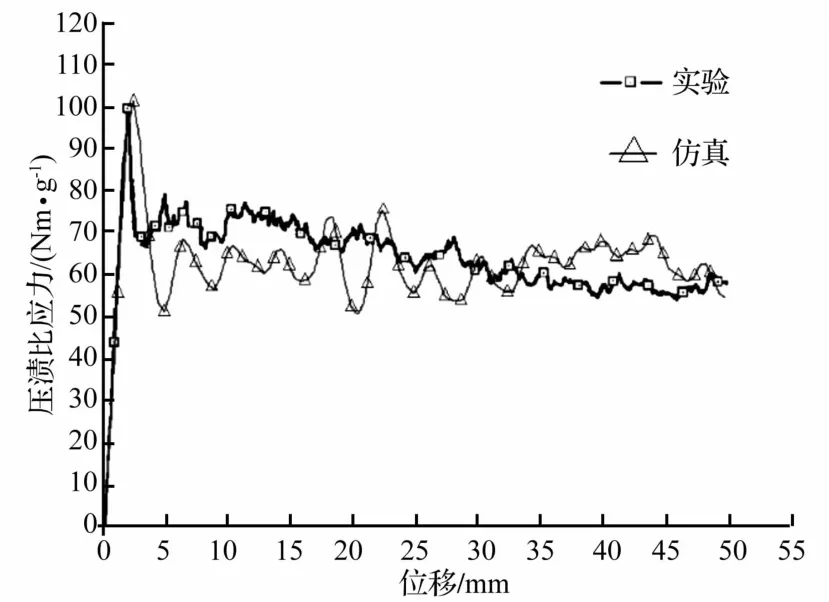
圖4 本文仿真與文獻［6］中實驗所得壓潰比應力－位移曲線Fig．4 Specific crushing stress-displacement curve

表3 實驗與仿真所得吸能數據Tab.3 Energy absorption data of test and simulation

5.3 考慮尺寸不確定性圓管吸能特性分析

受加工工藝影響復合材料薄壁結構的特征尺寸存在較大分散性，這會對結構的吸能特性造成影響，將對考慮尺寸不確定性的復合材料薄壁圓管進行吸能特性分析。

根據HB5800－99未注尺寸公差極限偏差中對公差要求可知圓管加工尺寸為高100±0．43，內徑為500－0．3，壁厚為1．840．12－0．12。

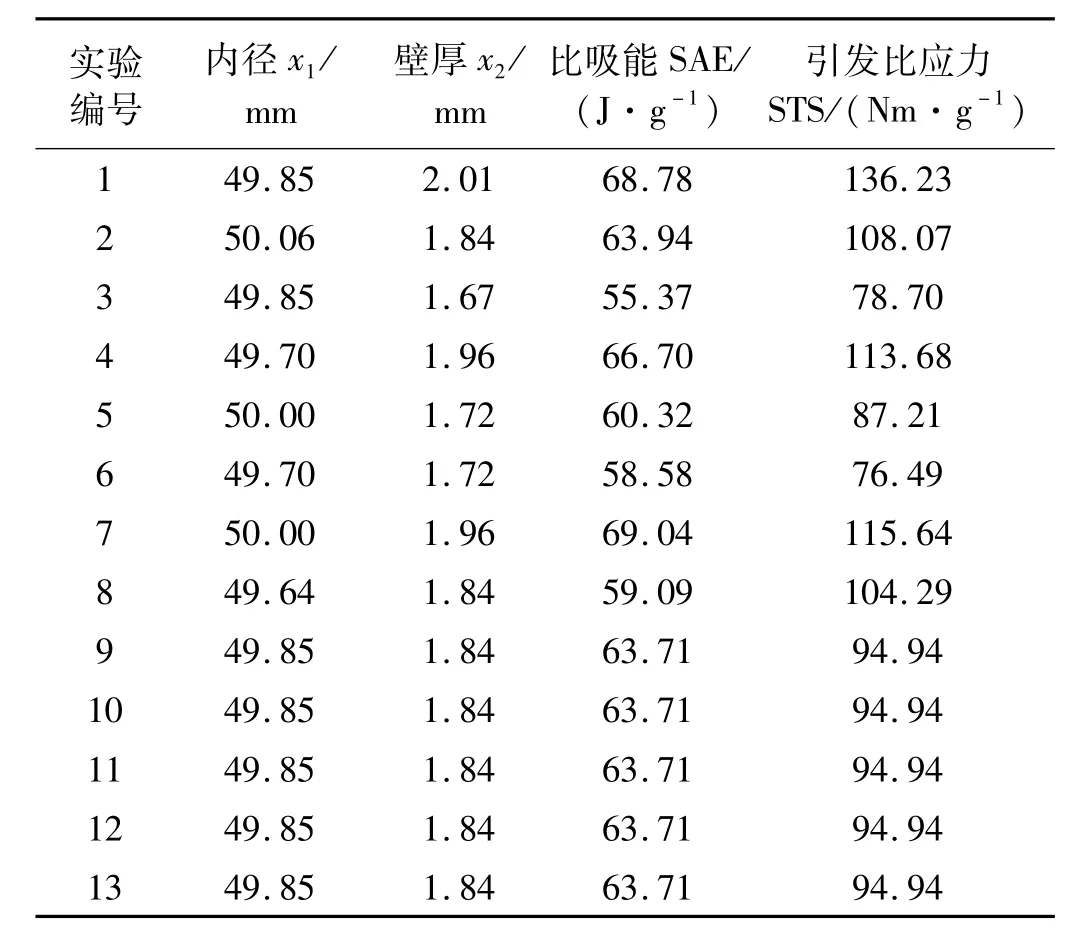
表4 實驗點安排及計算響應值Tab.4 Test points arrangement and respond value calculation

比吸能和引發比應力的計算并不涉及結構整體高度，且在當前高度的變化范圍內結構失效模式不會發生變化，為此高度方向的公差對吸能數據沒有影響，因而在進行吸能特性計算時不考慮高度的不確定性。考慮內徑和壁厚的分布區間x1I＝［49．7，50］，x2I＝［1．72，1．96］進行中心組合試驗設計方法安排實驗點，并利用前述仿真模型計算實驗點的響應值見表4。

利用表4中數據，根據式（2）～式（7）確定響應面形式和待定系數值，得到響應面方程和響應面圖。

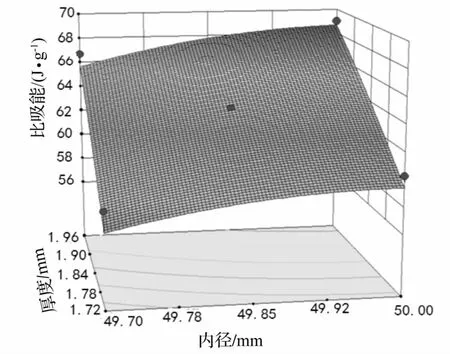
圖5 比吸能響應面圖Fig．5 The response surface figure of SAE

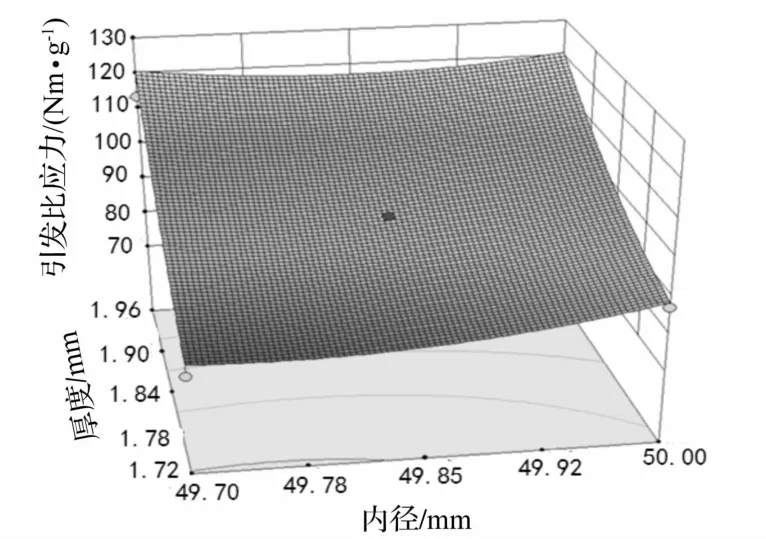
圖6 引發比應力響應面圖Fig．6 The response surface figure of TSS

根據式（8）對所得兩個響應面方程進行R2檢驗R21＝0．957 9、R22＝0．941 0表明該響應面方程擬合度較好。

根據響應面方程和參數分布區間按照式（9）～式（11）確定該復合材料圓管比吸能和引發比應力的分布區間為SAE∈［56．84，70．58］，TSS∈［64．524，125．36］。根據式（12）計算SAE和TSS的區間分散度分別為0．11和0．32。由此可知：結構尺寸公差對引發比應力的影響更加顯著。

文獻［6］中加工了2個名義尺寸為D＝50，h＝1．84的復合材料圓管，其實際尺寸分別為D＝50，h＝1．84和D＝50，h＝1．82，材料體系與鋪層方式均與本算例相同。并進行了壓潰實驗，所得比吸能分別為64．05 J／g和61．40 J／g，引發比應力分別為101．44 Nm／g和106．85 Nm／g。兩次實驗結果，均在估計的區間內，驗證了所提方法的有效性。

僅考慮內徑存在公差時xI1＝［49．7，50］，x2＝1．84，根據響應面方程和參數分布區間按照公式（9）～（11）進行計算得到比吸能區間為R11＝［61．69，65．73］，分散度K11＝0．03，引發比應力區間為R21＝［89．21，100．67］，分散度K21＝0．06。僅考慮壁厚存在公差時x1＝50，xI2＝［1．72，1．96］根據響應面方程和參數分布區間按照式（9）～式（11）進行計算得到比吸能區間為R12＝［59．00，68．42］，分散度K12＝0．07，引發比應力區間為R22＝［72．45，117．43］，分散度K22＝0．23。由此可知壁厚變化對結構吸能特性的影響要大于內徑，因而為減小結構吸能特性指標的波動，應在條件允許的范圍內盡可能提高壁厚的加工精度。

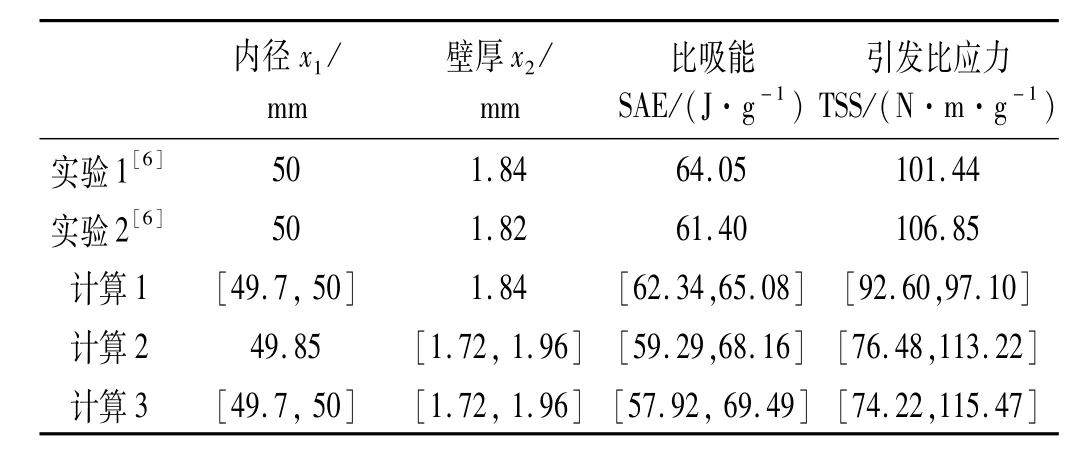
表5 實驗與本分析方法所得結果Tab.5 Results of test and analysismethod

6 結 論

針對復合材料吸能薄壁結構存在較大不確定性，難以通過簡單的實驗或仿真確定其吸能特性的問題，提出了一種基于區間的復合材料薄壁結構吸能特性評估方法。本方法只需要不確定參數的上下界，不需要參數的分布特征，通過有限個實驗點擬合響應面方程，不需要參數與響應間的函數關系，實用性較強。

采用響應面方法和中心組合實驗設計方法，通過較小的計算量的解決了復合材料薄壁結構吸能特性指標與結構參數間沒有通用的函數關系的問題，得到了擬合度較好的響應面方程。

在復合材料薄壁圓管結構的特征尺寸中，壁厚的不確定性對吸能特性的影響比內徑的影響更為明顯。壁厚的不確定性會對復合材料薄壁圓管引發比應力的影響要比對比吸能的影響更加顯著。因此，在設計觸發吸能圓管壓潰的初始峰值時，要注意對圓管壁厚公差的控制。

［1］張弘，魏榕祥．通用飛機抗墜撞設計指南［M］．北京：航空工業出版社，2009．

［2］Fasanella E L．Multi-terrain impact testing and simulation of a composite energy absorbing fuselage section［R］．American Helicopter Society 60th Annual Forum．Baltimore：MD，2004．

［3］Mamalis A G．Crashworthy characteristics of axially statically compressed thin-walled square CFRP composite tubes：experimental［J］．Composite Structures，2004，63：347－360．

［4］Xiao Xin-ran．Modeling energy absorption with a damage mechanics based composite material model［J］．Journal of Composite Materials，2009，43：427－244．

［5］盧子興，王曉英，俸翔．復合材料層合板臨界屈曲載荷分散性［J］．復合材料學報，2013，30（1）：194－200．

LU Zi-xing，WANG Xiao-ying，FENG Xiang．Critiacl bucking load discrepancy of composite laminates［J］．Acta Materiae Compositae Sinica，2013，30（1）：194－200．

［6］Huang J C，Wang X W．Numerical and experimental investigations on the axial crushing response of composite tubes［J］．Composite Structures，2009，91：222－228．

［7］龔俊杰，王鑫偉．復合材料波紋梁吸能能力的數值模擬［J］．航空學報，2005，26（3）：298－302．

GONG Jun-jie，WANG Xin-wei．Numerical simulation of energy absorption capability of composite waved beams［J］．Acta Aeronautica et Astronautica Sinica，2005，26（3）：298－302．

［8］Joosten MW，Dutton S，Kelly D，et al．Experimental and numerical investigation of the crushing responseof an open section composite energy absorbing element［J］．Composite Structures，2011，93：682－689．

［9］張麗娟，邱志平．含不確定參數的復合材料層合板屈曲的兩種非概率方法［J］．工程與建設，2008，22（3）：293－295．

ZHANG li-juan，QIU Zhi-ping．Two Non-probabilitymethods buckling analysis of composite laminated with uncertain parameters［J］．Engineering and Construction，2008，22（3）：293－295．

［10］苑凱華，邱志平．含不確定參數的復合材料壁板熱顫振分析［J］．航空學報，2010，31（3）：119－124．

YUAN Kai-hua，QIU Zhi-ping．Thermal flutter analysis of composite panel with uncertain parameters［J］．Acta Aeronautica et Astronautica Sinica，2010，31（3）：119－124．

［11］Salehghaffari S，Rais-Rohani M．Evidence-based design optimization of energy absorbing components under material field uncertainty［A］．53rd AIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics and Materials Conference［C］／／2012，Honolulu，Hawaii．

［12］王青春，范子杰．利用Ls-Dyna計算結構準靜態壓潰的改進方法［J］．力學與實踐，2003，25（3）：20－23．

WANG Qing-chun，FAN Zhi-jie．Improvement in anslysis of quasi-static collapase with Ls-Dyna［J］．Mechanics in Engineering，2003，25（3）：20－23．

Evaluation method for energy-absorbing composite structureswith uncertain parameters

FENG Zhen-yu，ZHAO Yan-qiang，CHEN Yan-fen，XIE Jiang
（Tianjin Key Laboratory of Civil Aircraft Airworthiness and Maintenance，Civil Aviation University of China，Tianjin 300300，China）

Due to the large dispersion ofmaterial properties and inherentmachining tolerance，uncertain factors should be considered in designing and analyzing composite structures．An evaluation method for energy-absorbing characteristics of thin-walled composite structures with uncertain parameters was proposed and developed herein．Thinwalled composite tubes extensively applied in automobile and aircraft engineering are typical crushable elements for absorbing collision energy．The uncertainties due to machining tolerance of thickness and inner diameter of a tube were considered in the present paper and represented by an interval model．Triggering Specific Stress（TSS）and Specific Energy Absorption（SEA）were concerned and calculated by finite element method for indicating energy-absorbing characteristics of the specimen under quasi-static axial crushing．Response surface method was then used to build a second-order function between uncertain parameters and the two indicators of energy-absorbing characteristics．Interval perturbation of the response surface function was at last performed to establish the intervals of TSS and SEA respectively．The results show that，compared to SEA，TSS ismore affected by the uncertainty ofwall thickness and inner diameter．In addition，the effectof uncertainty ofwall thickness on energy-absorbing characteristics ismore significant than thatof inner diameter．The investigation reveals that themachining tolerance of composite tube should be limited as low as possible to keep designed energy-absorbing characteristics．

thin-walled composite structures；energy-absorbing characteristics；uncertainty；intervalmodel；finite element analysis

TB332

A

10．13465／j．cnki．jvs．2015．12．002

中央高校項目（ZXH2012B004）；中國民航局科技項目（MHRD20140207）

2014－04－21 修改稿收到日期：2014－06－13

馮振宇 男，博士，教授，1966年生