一種改進Mathieu方程動力不穩定邊界的方法

王杰方，安偉光，宋向華

（哈爾濱工程大學航天工程系，哈爾濱 150001）

一種改進Mathieu方程動力不穩定邊界的方法

王杰方，安偉光，宋向華

（哈爾濱工程大學航天工程系，哈爾濱 150001）

基于Mathieu方程的臨界頻率方程式，提出了一種改進Mathieu方程不穩定邊界的方法，并獲得了比Bolotin近似邊界更精確的前三階收斂的不穩定邊界。從改進的不穩定區域邊界表達式和Bolotin近似公式的對比中發現：兩種方法獲得的第一、二階不穩定區域相差不大，但相較于Bolotin的第三階不穩定區域，改進的第三階不穩定區域整體上移，且上移幅度隨著激發系數的增大而增大。當激發系數μ取0．5時，上邊界上移幅度為8．61%，下邊界上移幅度為11．56%。對于受低頻載荷作用的動力穩定性問題，第三階不穩定邊界公式的改進具有重要的意義。

動力穩定性；Mathieu方程；臨界頻率；動力不穩定區域

Mathieu方程式常見于物理和工程的各個領域中：趙晶瑞［1］對一種新型的深海順應式采油平臺（Spar平臺）的縱搖運動進行了分析，得到了具有三次非線性項的有阻尼Mathieu方程。另外，在載流薄板的磁彈性動力屈曲問題中也存在Mathieu方程［2］。Li等［3］利用Mathieu方程分析了諧振式慣性傳感器的動力學特性。Mathieu方程有一個最重要的性質：當它們的系數間存在某種關系時，方程式具有無限增長的解，這些解在對應的參數平面上完全布滿了許多區域，這些區域相當于不穩定區域［4］。因此，確定不穩定區域是研究Mathieu方程問題的重點。

現有文獻中關于不穩定區域的分析方法主要有攝動法和傅里葉分析法［5］：攝動法［6］適用于小參數的情況，傅里葉分析法［7－8］適用于大參數的情況，例如，在實際的海洋環境下，Mathieu方程中的參數不再是小參數［5，9］，攝動法不再適用，需要采用傅里葉分析法。由于不穩定區在任何工程或者物理問題中都屬于必須避開的禁區，因此其精確性是十分重要的。文中將對目前廣泛采用的傅里葉分析法進行改進，推導出比文獻［4］中的Bolotin近似公式更精確的不穩定邊界公式。

本文思路是：將周期解按傅里葉級數展開并代入Mathieu方程中得到臨界頻率方程式，依次從臨界頻率方程式中提取n階前主子行列式等式，然后將其轉化為一元n次方程（n≤4），通過多次直接求解一元n次方程的根來獲得收斂的不穩定邊界表達式。

1 結構動力穩定性問題

1.1 結構動力穩定性問題的Mathieu方程

以簡諧縱向力P＝P0（1+βcos（θt））作用下的鉸支直桿的動力穩定性問題為例［4］，其Mathieu方程為

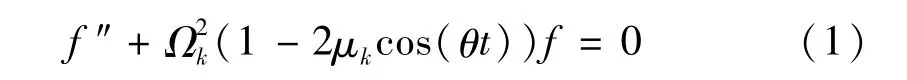
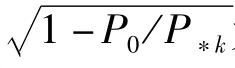
從靜力屈曲角度：縱向力的最大值Pmax＝（1+ β）P0須小于臨界屈曲載荷p*1，即P0須小于P*1／（1+ β）。假設P0＝P*1／（1+β），代入μk中得，β取任意值時，激發系數μ恒等于0．5。由于μk是隨P0單調遞增的函數，所以激發系數μk的取值范圍為（0，0．5）。

Mathieu方程存在周期為T和2T的周期解，且周期相同的兩個解包圍著不穩定區，周期不同的兩個解包圍著穩定區。因此，找出使Mathieu方程具有周期T和2T的周期解的條件就可以確定不穩定邊界［4］。

1.2 與周期為2T的周期解對應的臨界頻率方程式

將Mathieu方程的解展開為

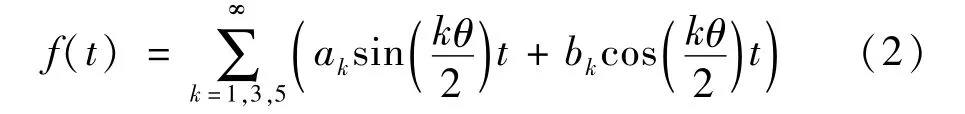
并代入Mathieu方程中，得到與周期2T的周期解對應的臨界頻率方程式為

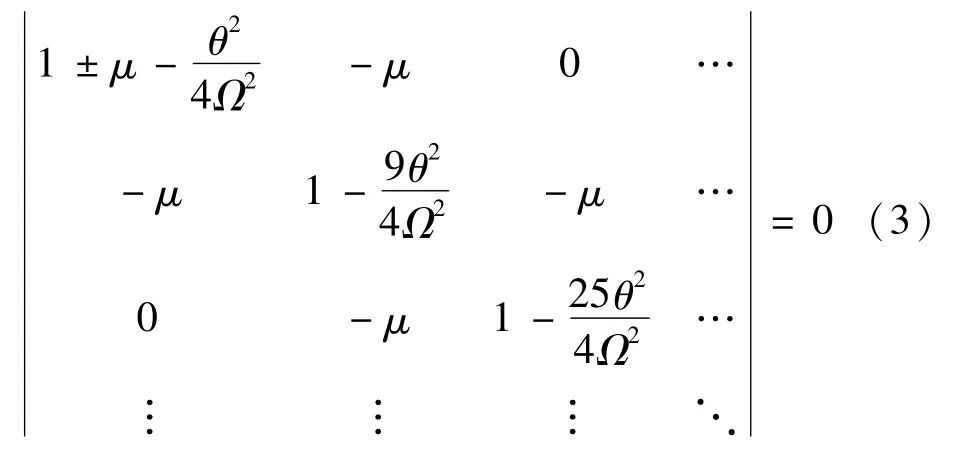
周期2T的周期解包圍的不穩定區域由式（3）確定。

1.3 與周期為T的周期解對應的臨界頻率方程式

同樣，將Mathieu方程的解展開為

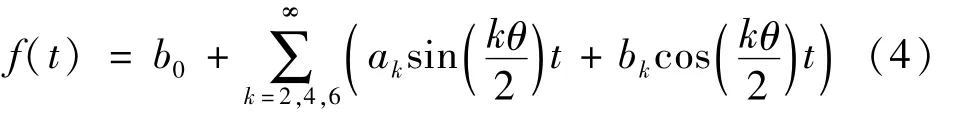
得到與周期T的周期解對應的臨界頻率方程式

周期T的周期解包圍的不穩定區由式（5），式（6）確定。

2 改進Mathieu方程不穩定邊界的方法

2．1 與周期2T的周期解對應的動力不穩定區域邊界

（1）若式（2）中的系數a1，b1存在非零解，其他系數為0，對應于式（3）的左上角的對角線元素為0，從而獲得第一階動力不穩定區域的邊界表達式

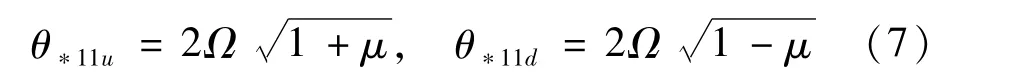
式中：u表示上邊界，d表示下邊界，θ*iju表示第j次計算的第i階上邊界，j表示第j次計算的不穩定邊界，下同。上式中的第一階動力不穩定區域邊界表達式是關于Mathieu方程存在周期為2T的周期解嚴格成立的條件，但它們并不是完整的第一階不穩定區域的邊界。下面將會對第一階不穩定區域的邊界表達式進行進一步的推導計算和修正，以獲得完整的、收斂的第一階不穩定區域邊界。

（2）若式（2）中的系數a1，b1，a3，b3存在非零解，其他系數為0，對應于式（3）中2階前主子行列式等于0，得到第二個第一階動力不穩定區域的邊界

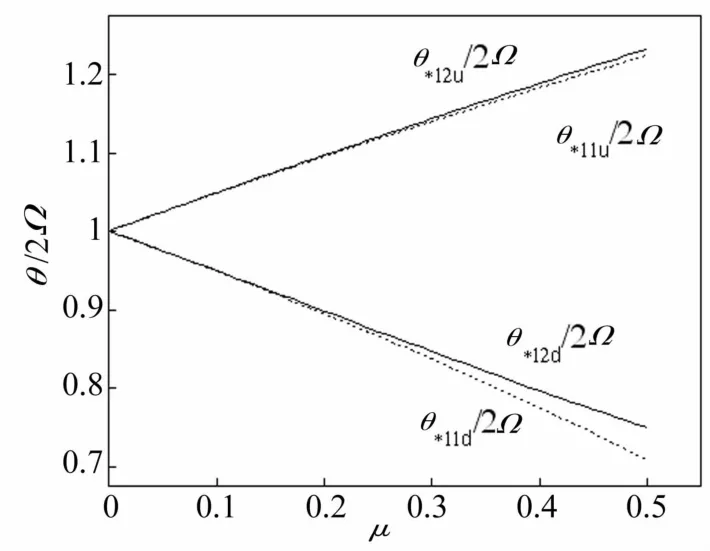
圖1 第一次修正后的第一階不穩定區域Fig．1 The first order unstable region after the first amend

從圖1可知，上邊界θ*12u在 θ*11u之上，下邊界θ*12d包含在θ*11d之內，所以經第一修正后的第一階不穩定區域的邊界為 (θ*12u，θ*11d)。

（3）若式（2）中的系數a1，a3，a5和b1，b3，b5，存在非零解，其他系數為0，對應于式（3）中3階前主子行列式等于0，將它們化為兩個標準的一元三次方程，

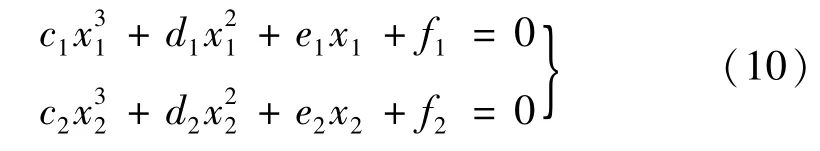
式中：x1＝x2＝θ2／4Ω2。

采用盛金公式求解上述兩個一元三次方程的根，即可獲得不穩定區域的邊界公式。盛金判別式為

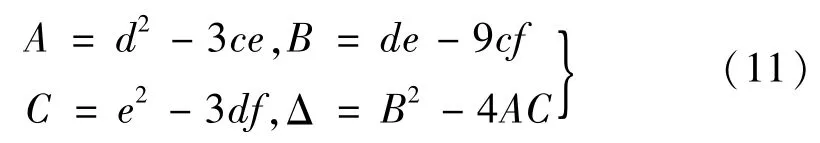
第三個第一階動力不穩定區域的邊界為

圖2給出了將不穩定區（θ*32u，θ*32d）與（θ*31u，θ*31d）整合后得到的第一次修正的第三階動力不穩定區域。

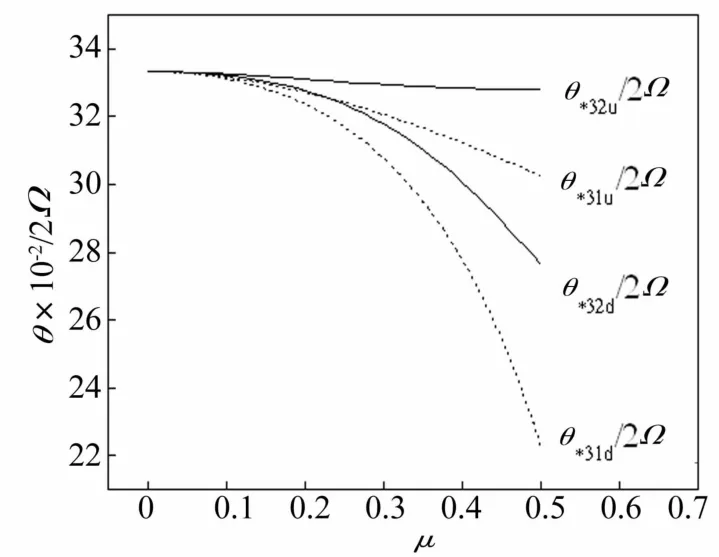
圖2 第一修正后的第三階不穩定區域Fig．2 The third order unstable region after the first amend

從圖2可知，第三階不穩定區域的上邊界θ*32u在θ*31u之上，下邊界θ*32d包含在下邊界θ*31d之內，所以，經第一次修正后的第三階不穩定區域的邊界為（θ*32u， θ*31d）。另外，經計算發現θ*13u和θ*13d的值與上文中的θ*12u和θ*12d非常相近，這說明第一次修正后得到的邊界（θ*12u，θ*11d）是已經收斂的邊界，因此并不需要對第一階不穩定區進行第二次修正。收斂的第一階不穩定區域的邊界表達式為

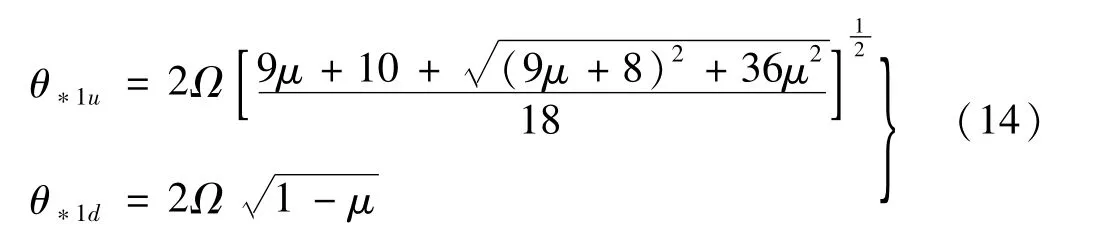
（4）若式（2）中的系數a1，a3，a5，a7和b1，b3，b5，b7存在非零解，其他系數為0，即式（3）中4階前主子行列式等于0，將這兩個4階行列式等式化為標準的一元四次方程，

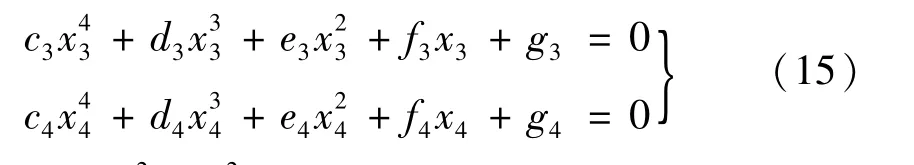
式中：x3＝x4＝θ2／4Ω2。

采用置換群解法求解上述兩個一元四次方程的根即可獲得不穩定區邊界。置換群法的相關判別式為

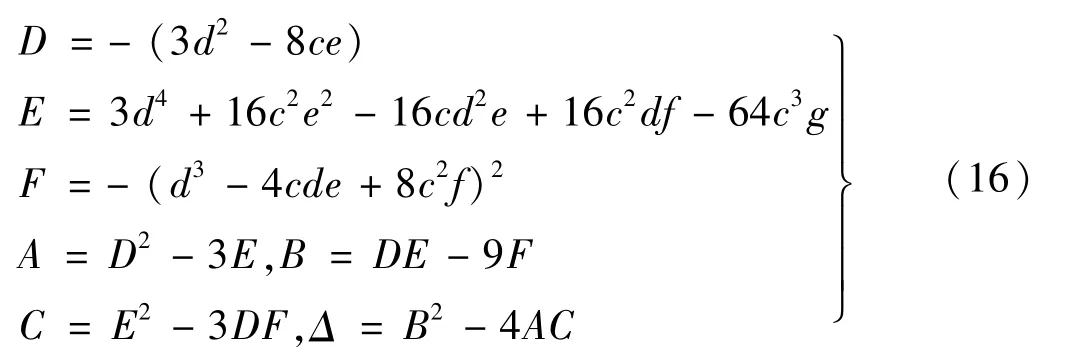
第三個第三階動力不穩定區域的邊界

當μ∈［0，0．5］時，θ*14u和θ*14d的值與上文中的θ*13u和θ*13d幾乎一致，這也再一次驗證了式（14）是收斂的。當μ∈［0，0．5］時，θ*33u的值略高于θ*32u（激發系數取0．5時，變化幅度僅為0．3%），因此第三階動力不穩定區域的邊界仍為（θ*32u，θ*31d）。最終得到收斂的第三階動力不穩定區域的上下邊界表達式為

2．2 與周期T的周期解對應的動力不穩定區域邊界

（1）式（5）的左上角的對角線元素為0，式（6）中2階前主子行列式為0，得

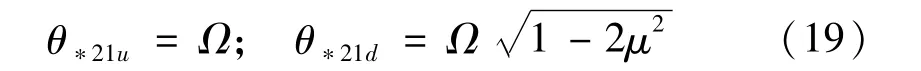
（2）式（5）中的2階前主子行列式為0，式（6）中

3階前主子行列式為0，得到第二個第二階動力不穩定區域的邊界

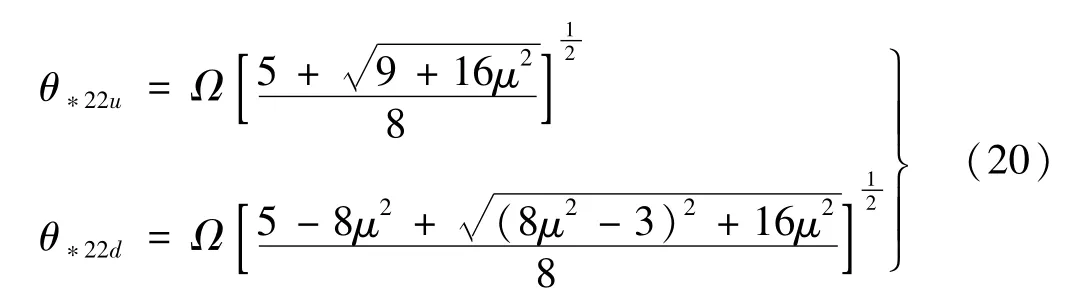
將（θ*22u，θ*22d）與（θ*21u，θ*21d）整合起來得到第一次修正后的第二階動力不穩定區域見圖3。

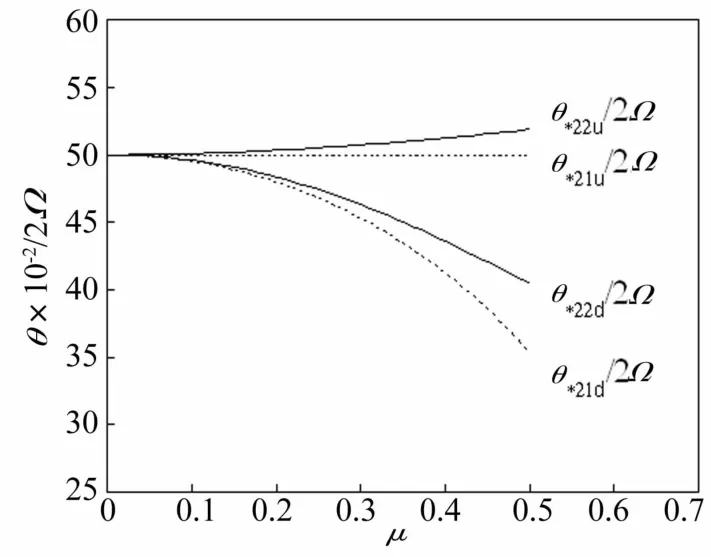
圖3 第一次修正后的第二階不穩定區域Fig．3 The second order unstable region after the first amend

從圖3可知，第二階不穩定區域的上邊界θ*22u在θ*21u之上，下邊界θ*22d包含在下邊界θ*21d之內，所以經第一修正后的第二階不穩定區域的邊界為（θ*22u，θ*21d）。

（3）式（5）中的3階前主子行列式為0，式（6）中4階前主子行列式為0，獲得兩個標準的一元三次方程，

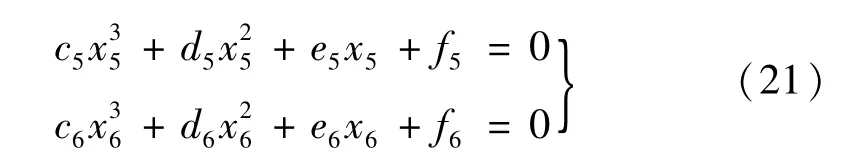
式中：x5＝x6＝θ2／Ω2。

采用盛金公式求解上述方程的根，能夠獲得第三個第二階動力不穩定區域的邊界

式中：θi，Ai的含義與式（12）和式（13）相同。

計算表明，當μ∈［0，0．5］時，θ*23u和θ*23d的所夾的不穩定區域被（θ*22u，θ*21d）包裹，因此不需要對第二階動力不穩定區邊界進行第二次修正。最終得到收斂的第二階動力不穩定區域的上下邊界表達式是

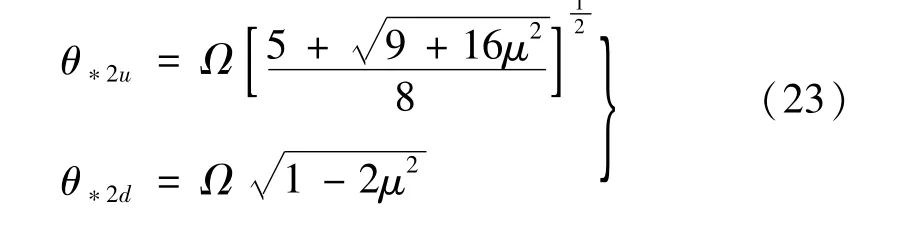
（4）式（5）中的4階前主子行列式為0，式（6）中5階前主子行列式為0，獲得兩個標準的一元四次方程，

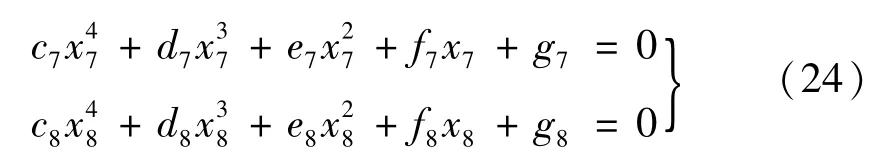
式中：x7＝x8＝θ2／Ω2。

采用置換群法求解上述方程的根，即可獲得第四個第二階動力不穩定區域的邊界

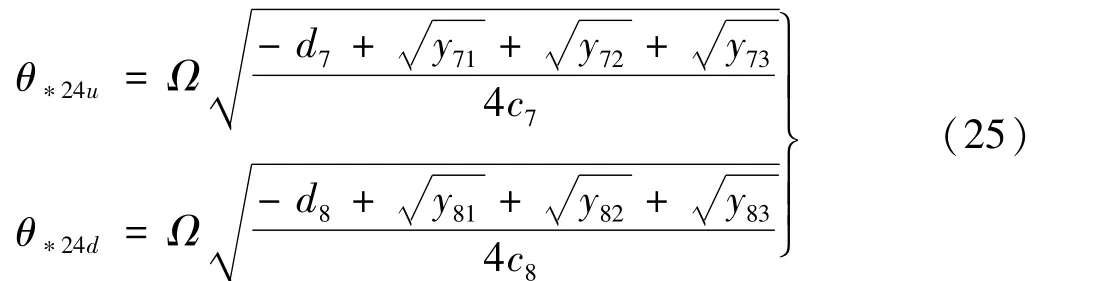
式中：yi1，yi2，yi3，θi的含義與式（17）中相同。

計算表明，在μ∈[0，0．]5范圍內，θ*24u和θ*24d的值與上文中的θ*23u和θ*23d幾乎一致，這也再一次驗證了式（23）的收斂性。

3 改進的不穩定邊界與Bolotin近似邊界比較

為了獲得收斂的前三階不穩定邊界，需要從臨界頻率方程式中提取的最高次方程為一元四次方程。經驗算，文中采用盛金公式求解一元三次方程的根和采用置換群法求解一元四次方程的根時，其誤差的數量級僅為10－15，完全可以認為每一步的求解過程并不產生誤差。不穩定邊界的誤差只與最終收斂情況有關，但邊界的收斂卻是可控的。文中的前三階不穩定邊界（式（14）、式（23）和式（18））經過多次修正已是收斂的邊界，因此采用本方法能獲得比Bolotin近似邊界更精確的表達式。

3.1 改進的不穩定邊界與Bolotin近似邊界的比較

將改進的前三階不穩定區域邊界表達式（14）、式（23）和式（18）與Bolotin前三階不穩定區域近似邊界公式［4］進行對比。圖4～圖6中分別給出了第一階、第二階、第三階改進的不穩定邊界和Bolotin近似邊界的曲線圖，實線表示改進的不穩定邊界，虛線表示Bolotin近似邊界。注意，由于本改進的第一階和第二階不穩定區域的下邊界表達式與Bolotin方法給出的邊界公式相同，因此，圖4和圖5中的下邊界只有一條實曲線。

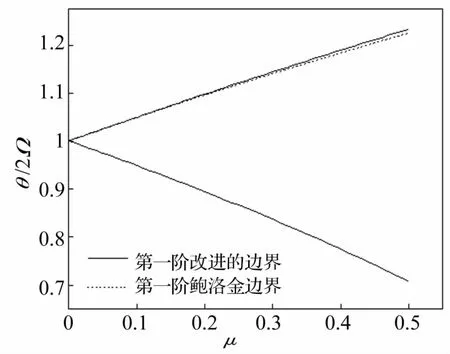
圖4 第一階不穩定區域的比較Fig．4 Comparison of the first order dynamic unstable region

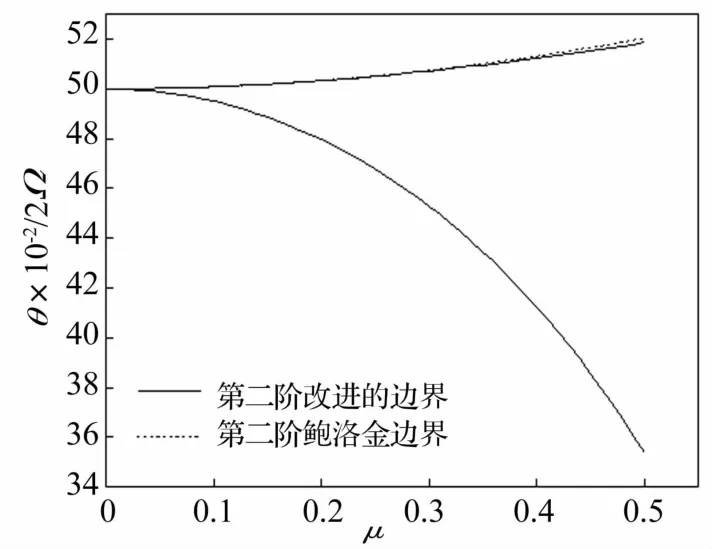
圖5 第二階不穩定區域的比較Fig．5 Comparison of the second order dynamic unstable region

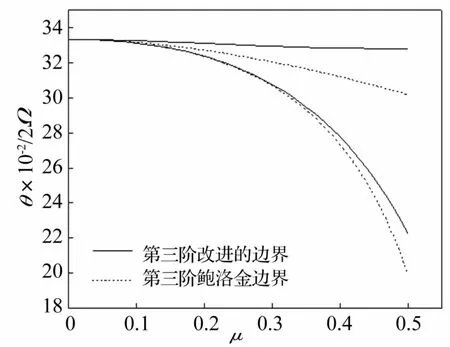
圖6 第三階不穩定區域的比較Fig．6 Comparison of the third order dynamic unstable region

從圖4和圖5中可知，對于第一階、第二階不穩定區域的上邊界，兩種計算方法得出的結果相差都不大。計算表明，當μ＝0．5時，兩種方法計算的第一階上邊界誤差僅為0．653%，第二階上邊界誤差也僅為－0．193%。這說明采用本方法獲得的第一階和第二階不穩定區邊界表達式的精確度是合理的。

從圖6可知，相較于第三階Bolotin不穩定區域，改進的第三階不穩定區域整體上移，且上移幅度隨著激發系數的增大而增大。當μ分別取0．1、0．2、0．3、0．4、0．5時，改進的第三階不穩定區域的上邊界較Bolotin的第三階上邊界的上移幅度分別為1．003%、1．223%、2．492%、5．128%、8．609%；當μ分別取0．1、0．2、0．3、0．4、0．5時，改進第三階不穩定區域的下邊界的上移幅度分別為0．0%、0．0%、0．326%、1．832%、11．558%，偏差較大，不能忽略。

3.2 第三階動力不穩定區域邊界改進的意義

以文獻［10］中的水下超空泡高速航行器為例：超空泡尾部脈動和尾渦脫落產生的空泡高頻特征頻率θ的取值范圍為80～160 Hz，航行器殼體的特征頻率ω＝149 Hz，分析航行器的動力不穩定區域與外載荷頻率之間的位置關系。

對于水下高速航行器的動力屈曲問題而言，其第一階不穩定區域位于2Ω附近，第二階不穩定區域位于Ω附近，第三階不穩定區域位于2Ω／3附近，用定值分量P0和臨界力P*表示為

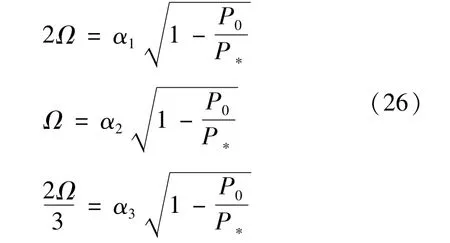
其中，臨界力只與結構參數有關，與周期力無關。α1，α2，α3依次為第一階、第二階、第三階不穩定區域邊界的系數，且α1＝298，α2＝149，α3＝99．3。下面的第一階、第二階、第三階不穩定區域上下邊界的系數依次用（α1u，α1d）、（α2u，α2d）、（α3u，α3d）來表示。由于μ＝0時，不穩定區域的上下邊界相等，所以上式的系數省略了下角標u和d。

表1給出了激發系數μ取不同值時，改進的前三階不穩定區域上下邊界系數（α1u，α1d），（α2u，α2d），（α3u，α3d）的值和第三階Bolotin不穩定邊界系數（α3u′，α3d′）。

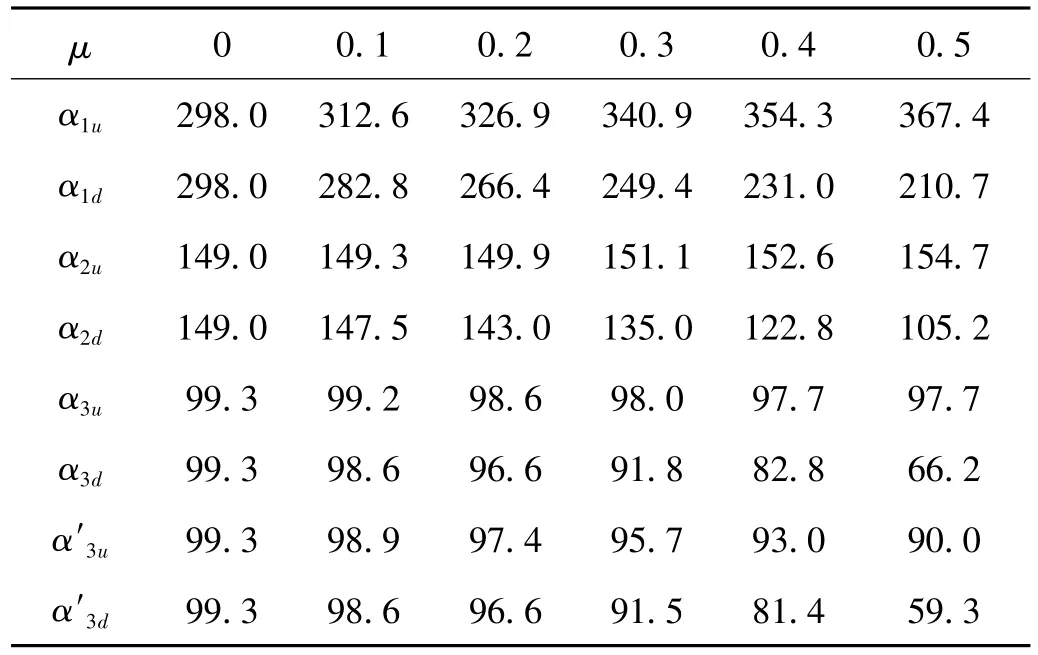
表1 前三階不穩定區域邊界的系數Tab.1 The coefficient of the first three order unstable region

以μ＝0．5時的不穩定區為例，結合表1中的數據，經計算發現：

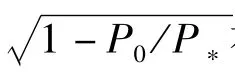
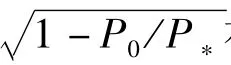
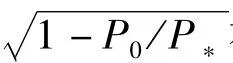
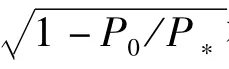
從以上四個結論可知：① 當P0／P*的值較大時，第一二階不穩定區與載荷頻率發生重合的可能性較大，是主要的不穩定區。② 當P0／P*的值較小時，第三階不穩定區域與外載荷頻率區間發生重合的可能性較大，也可能是主要的不穩定區域。且從“（3）”和“（4）”的對比中可知：采用改進的不穩定邊界表達式，P0／P*＞0．33時才能避開第三階不穩定區域，而采用Bolotin的近似邊界表達式時，P0／P*＞0．21時就能避開第三階不穩定區域。也就是說，采用Bolotin的近似邊界表達式認為(0．21，0．33)是P0／P*的安全取值范圍，但采用改進的第三階不穩定表達式認為(0．21，0．33)是P0／P*的危險取值范圍。這說明采用精度更高的改進不穩定邊界使結構避免了采用Bolotin近似公式時所隱藏的危險。

4 超空泡運動體圓柱薄殼艙段的動力穩定性分析算例

超空泡運動體航行深度H＝10 m，流場密度ρw＝1 000 kg／m3，對于自然超空泡，空泡內的飽和蒸汽壓pc＝2 350 Pa（20°C），標準大氣壓p＝101 325 Pa。圓柱薄殼艙段的幾何參數：半徑R＝0．2 m，長度L＝4 m，厚度h＝3 mm，空化器直徑dn＝0．2 m。材料物理參數：彈性模量E＝209 GPa，材料密度ρ＝7 850 kg／m3，泊松比ν＝0．3。

基于文獻［11］中圓柱薄殼動力穩定性微分方程，采用Bolotin方法和本方法計算超空泡運動體圓柱艙段的動力不穩定區。圖7～圖9給出了i＝1，k＝1（i，k分別為軸向和周向的半波數）時，依賴于航行速度V（m／s）和頻率f／Hz的前三階動力不穩定區域。

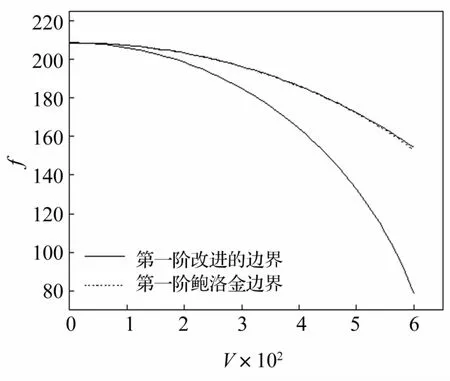
圖7 第一階不穩定區域的比較Fig．7 Comparison of the first order dynamic unstable region

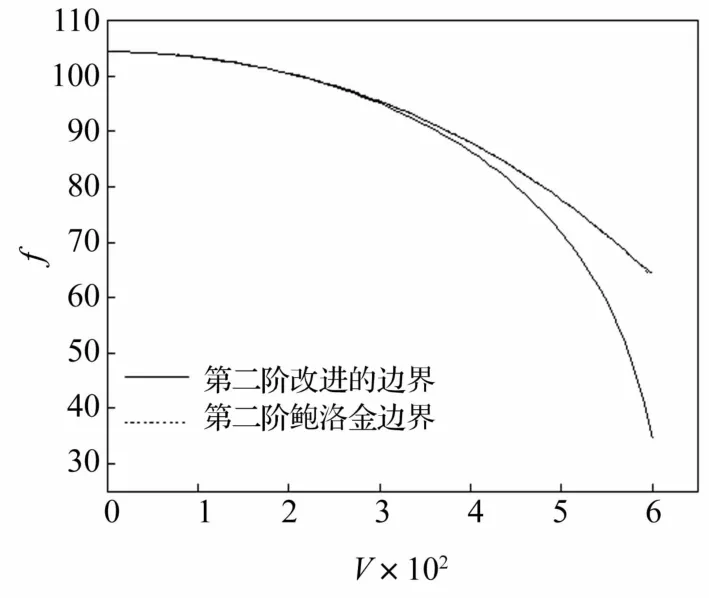
圖8 第二階不穩定區域的比較Fig．8 Comparison of the second order dynamic unstable region

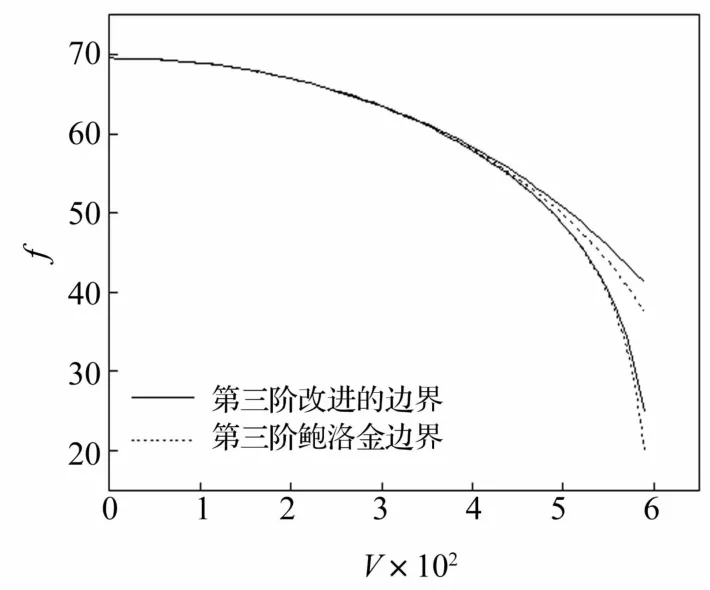
圖9 第三階不穩定區域的比較Fig．9 Comparison of the third order dynamic unstable region

從圖7～圖9可知，隨著航行速度的增大，超空泡運動體圓柱薄殼艙段的不穩定區間寬度也在不斷地增大。由圖7和圖8可知，對于第一階和第二階不穩定區域，采用Bolotin方法和本方法獲得的結果相差甚小，可以忽略；但是，從圖9可知，采用本文方法獲得的不穩定區較Bolotin方法獲得的不穩定區整體上移，且航行速度越大上移幅度越大，這一結論與3．1節中的結論是一致的。

5 結 論

本文是采用多次直接求解一元n次方程的根來獲得不穩定邊界表達式的。首先，利用盛金公式求解一元三次方程的根和置換群法求解一元四次方程的根時，其誤差的數量級僅為10－15，完全可以認為每一步的求解并不產生誤差；其次，文中的前三階不穩定邊界經過多次修正已是收斂的邊界。以上兩點確保了本文改進方法的精確度。并得出以下結論：

（1）從改進的不穩定區域邊界表達式和Bolotin近似公式的對比中發現：兩種方法獲得的第一階、第二階動力不穩定區域相差不大；相較于第三階Bolotin不穩定區域，本文方法獲得的改進的第三階不穩定區域整體上移，且上移幅度隨著激發系數的增大而增大，當μ＝0．5時，上邊界上移幅度為8．61%，下邊界上移幅度為11．56%。

（2）從水下超空泡高速航行器的動力穩定性分析算例中可知：當P0／P*的值較小時，第三階不穩定區域與外載荷頻率區間發生重合的可能性較大，也可能是主要的不穩定區域。

（3）采用精度更高的改進的不穩定邊界使結構避免了采用Bolotin不穩定近似公式時所隱藏的危險。

綜上所述，由改進的傅里葉分析法確定的不穩定區邊界的精度，為Mathieu方程的動力不穩定區提供了比Bolotin不穩定區域更精確的邊界表達式。

［1］趙晶瑞，唐友剛，王文杰．傳統Spar平臺參數激勵Mathieu不穩定性的研究［J］．工程力學，2010，27（3）：222－227．

ZHAO Jing-rui，TANG You-gang，WANGWen-jie．Study on the parametrically excited mathieu instability of a classic spar platform［J］．Engineering Mechanics，2010，27（3）：222－227．

［2］王平，王知人，白象忠．馬丟方程解的穩定性在磁彈性屈曲中的應用［J］．哈爾濱工業大學學報，2009，41（11）：222－224．

WANG Ping，WANG Zhi-ren，BAI Xiang-zhong．Applications of the stability of Mathieu equation's solution in magnetic-elastisity buckling problem［J］．Journal of Harbin Institute of Technology，2009，41（11）：222－224．

［3］Li Yan，Fan Shang-chun，Guo Zhan-she．Mathieu equation with application to analysis of dynamic characteristics of resonant inertial sensors［J］．Commun Nonlinear Sci Numer Simulat，2013，18：401－410．

［4］Bolotin，V V．The Dynamic Stability of Elstic Systems［M］．Holen-Day San Francisco，1964．

［5］徐萬海，吳應湘，鐘興福，等．海洋細長結構參數激勵不穩定區的確定方法［J］．振動與沖擊，2011，30（9）：79－83．

XU Wan-hai，WU Ying-xiang，ZHONG Xing-fu，et al．Methods for parametric excitation instability analysis of slender flexible cylindrical structures in offshore engineering［J］．Journal of Vibration and Shock，2011，30（9）：79－83．

［6］Nayfeh A H．Introduction to Perturbation Technique［M］．New York：Wiley，1981．

［7］馮世寧，陳浩然．含分層損傷復合材料層合板非線性動力穩定性［J］．復合材料學報，2006，23（1）：154－160．

FENG Shi-ning，CHEN Hao-ran．Nonlinear dynamic instability behavior of delaminated composite laminates［J］．Acta Materiae Compositae Sinica，2006，23（1）：154－160．

［8］趙洪金，董寧娟，劉超，等．基于能量法的高溫（火災）環境下軸心受壓格構柱動力穩定性分析［J］．工 程 力 學，2011，28（12）：160－165．

ZHAO Hong-jin，DONG Ning-juan，LIU Chao，et al．Dynamic stability analysis on axial compression lattice column under high temperature condition using energy method［J］．Engineering Mechanics，2011，28（12）：160－165．

［9］王俊榮，謝彬．深水半潛式平臺Mathieu不穩定問題研究［J］．工程力學，2012，29（10）：347－353．

WANG Jun-rong，XIE Bin．Mathieu instablity study of a deepwater semi-submersible platform［J］．Engineering Mechanics，2012，29（10）：347－353．

［10］黨建軍，張謀，郭芳，等．超空泡脈動對水下高速航行器殼體強度的影響研究［J］．機械科學與技術，2011，30（11）：1930－1933．

DANG Jian-jun，ZHANG Mou，GUO Fang，et al．A study of the influence of the super-cavit pulsation on the intensity of the shell of the high-speed underwater vehicle［J］．Mechanical Science and Technology for Aerospace Engineering，2011，30（11）：1930－1933．

［11］王杰方，安偉光，宋向華．超空泡運動體圓柱薄殼動力屈曲及可靠性分析［J］．振動與沖擊，2014，33（8）：22－28．

WANG Jie-fang，AN Wei-guang，SONG Xiang-hua．Dynamic buckling and reliability analysis of a cylindrical thin shell for supercavitating vehicles［J］．Journal of Vibration and Shock，2014，33（8）：22－28．

Im proved method about dynam ic unstable boundary ofmathieu equation

WANG Jie-fang，ANWei-guang，SONG Xiang-hua
（Department of Aerospace Engineering，Harbin Engineering University，Harbin 150001，China）

An improvedmethod about unstable boundary of Mathieu equation was proposed according to the critical frequency equation，and the first three orders convergent unstable boundary was got，which ismore accurate than the Bolotin approximate boundary．Comparing the twomethods，it shows that their first two orders dynamic unstable region are almost the same，the third order unstable region of the improved method moves upward compared with the Bolotinmethod，and the range is amplified with the growth of excitation coefficient．When the excitation coefficientμis 0．5，the upper boundarymoves upward about8．61%and the lower boundary moves upward about 11．56%．With respect the dynamic stability problem caused by low frequency loading，the improvement on the third order unstable boundary expression has great significance．

dynamic stability；mathieu equation；critical frequency；dynamic unstable region

O342

A

10．13465／j．cnki．jvs．2015．12．031

國家科技部國際合作專項（2012DFR00070）

2014－04－28 修改稿收到日期：2014－05－27第一作者王杰方女，博士，1987年生

安偉光 男，教授，博士生導師，1943年生

郵箱：anweiguang＠hrbeu．edu．cn