基于貝葉斯理論的結構動力可靠度更新方法與分析

劉 佩

（1．北京交通大學土木建筑工程學院，北京 100044；2．結構風工程與城市風環境北京市重點實驗室，北京 100044）

基于貝葉斯理論的結構動力可靠度更新方法與分析

劉 佩1，2

（1．北京交通大學土木建筑工程學院，北京 100044；2．結構風工程與城市風環境北京市重點實驗室，北京 100044）

通過一種基于結構動力測試數據和貝葉斯理論的方法來更新結構可靠度。該方法考慮了結構可能受到的激勵和結構模型及其參數的不確定性，利用結構在服役期間的動力測試數據，通過貝葉斯概率方法對結構參數進行了識別。利用拉普拉斯漸近估計解法，對僅根據設計條件得到的結構可靠度進行了更新。對受隨機動荷載作用的某桁架結構在三種情況下的可靠度進行了計算：一為僅考慮荷載的隨機性，二為考慮荷載的隨機性和結構模型參數的先驗分布，三為考慮荷載的隨機性和結構模型參數的更新分布。比較了實際結構和有限元模型更新后的自振頻率和振型，并對更新的可靠度計算結果進行了分析。結果表明，與確定性名義模型的失效概率相比，測點處自由度的更新失效概率與真實值較為接近；未測試自由度的更新失效概率可能與真實值差別較大；增加測點數不一定改善失效概率的更新效果。

貝葉斯理論；動力可靠度；參數識別；失效概率；更新分布

在結構設計階段，所有影響結構安全性評估的不確定性因素都應該考慮。由于結構模型不可能代表真實的結構，結構模型誤差總是存在的，并且不存在模型參數的真實值。因此計算結構的可靠度時，除了考慮結構在服役過程中可能受到的隨機激勵的影響，還應考慮結構模型誤差及模型參數的不確定性。

對結構可靠度的評估不僅在結構的設計階段很重要，在結構的服役過程中也很重要。在服役過程中，由于結構的疲勞或者受到腐蝕，強風或地震引起結構構件或節點的損傷等原因，結構的狀態會發生改變，可靠度可能會降低。因此，在結構建成后，需要通過監測結構的動力響應來對結構的模型參數及可靠度進行重新估計。

利用結構在服役期間測試得到的動力響應來對結構模型參數進行識別，并對結構可靠度進行重新評估，優勢在于：測試時在結構工作狀態下即可進行；計算時不需要對結構模型的邊界條件進行假定；可能出現的結構材料及幾何非線性也可以在測得的反應中體現出來。

對結構模型參數進行識別以及計算結構的可靠度時，應考慮結構模型誤差及模型參數的不確定性。基于貝葉斯理論的系統識別方法［1－2］通過建立結構模型誤差的概率模型對結構模型的不確定性進行定量的描述，不僅可以得到指定動力荷載下更精確的結構反應，而且可以定量評估該精度，已被應用在結構模型修正及可靠度計算［3－4］、模態參數識別［5－9］、模型參數識別［10，11］、損傷識別［12－13］等方面。

基于貝葉斯理論和結構動力測試數據更新結構的可靠度，該方法可同時考慮結構所受隨機激勵以及結構模型和結構參數的不確定性。對某桁架有限元模型在隨機動荷載作用下三種情況的可靠度進行了計算：①采用確定性模型參數時，結構在隨機荷載作用下的可靠度。②考慮結構模型參數的先驗分布，結構在隨機荷載作用下的可靠度。③利用結構反應測試數據更新結構模型參數的概率分布后，結構在隨機荷載作用下的可靠度并將結構模型更新后的模態參數與實際情況進行了對比，對可靠度計算結果與測點位置和測點數的關系進行了討論。

1 基于貝葉斯理論更新結構模型參數

由于結構在服役期間特性可能發生改變，故可以利用結構的動力反應測試數據對結構的模型參數進行更新。模型參數的更新可以通過基于貝葉斯理論的系統識別法進行，該方法對結構模型參數及反應誤差進行概率描述，可以考慮由于測試噪聲及模型誤差引起的不確定性。

假定結構模型參數為θ；q（n；θ）表示在tn時刻結構模型中N0個自由度的反應，tn＝nΔt，n＝1，…，N，N為數據點數；y（n）表示在tn時刻結構中N0個自由度觀測到的反應；則y（n）＝q（n；θ）+e（n；θ），其中e（n；θ）為反應預測誤差，可通過參數σ表示。測試噪聲相比模型誤差要小很多，故僅考慮模型誤差對結構反應預測誤差的影響。

根據貝葉斯理論，設結構模型參數的先驗概率密度函數為f（θ），得到測試數據y后，結構模型參數的后驗概率密度函數（即更新的概率密度函數）

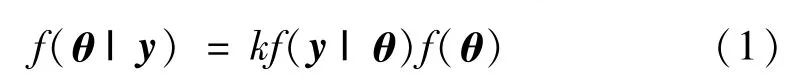
式中：k＝1／f（y），f（y｜θ）為似然函數，此概率密度函數與模型誤差e（n；θ）有關。假定模型誤差的概率模型為離散高斯白噪聲過程，其各元素相互獨立，均值為0，標準差為σ。則似然函數

對式（4）進行最小化運算，可得模型參數的最有可能值θ＾及對應的模型誤差標準差的最有可能值。

當存在唯一的模型參數最有可能值時，即為全局可識別問題時，模型參數更新的概率密度函數可以通過高斯分布進行估計，其均值為最有可能值θ＾，協方差矩陣可通過負對數似然函數的Hessian矩陣求得。

2 結構可靠度計算

2.1 確定性模型參數時的可靠度

若已知確定性的模型參數時，結構在隨機激勵下的失效概率為P（F｜θ），可通過Monte-Carlo法計算得到。

2.2 考慮模型參數先驗分布的可靠度

若考慮結構模型參數的不確定性，且結構實際的反應數據未知，可直接依據結構模型參數的先驗概率密度函數，由全概率定理得失效概率為：

式中：f（θ）可根據工程經驗選擇方便計算的數學形式。該失效概率可以根據拉普拉斯漸近估計解法求得［14］。令負對數似然函數l（θ）＝－ln P（F｜θ）－ln f（θ），對l（θ）進行最小化運算，可得模型參數的最有可能值θ，則失效概率

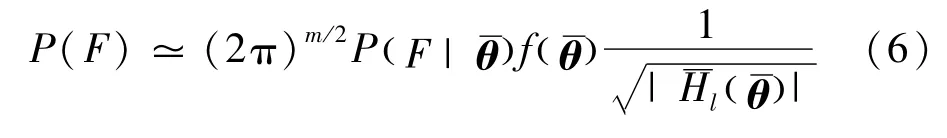
當模型參數服從正態分布時，模型參數的最有可能值為模型參數的均值，由式（6）得失效概率

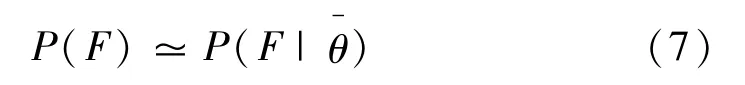
故結構實際的反應數據未知時，結構的失效概率可通過結構模型參數的最有可能值近似計算得到。

2.3 考慮模型參數后驗分布的可靠度

若考慮結構模型參數的不確定性，且得到結構實際的反應數據后，可根據結構模型參數的后驗分布，由全概率定理得更新的失效概率為：

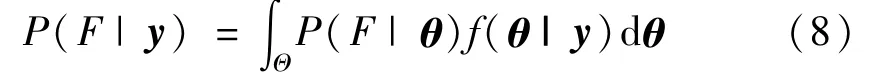
該失效概率可根據拉普拉斯漸近估計解法求得。當為全局可識別情況時，式（8）可寫為

故得到結構實際的反應數據后，結構更新的失效概率可通過結構模型參數的最有可能值近似計算得到。

3 桁架結構的更新可靠度計算與分析

某桁架結構由7根桿件及5個節點構成，具體尺寸、節點編號、桿件編號、自由度編號見圖1。結構在節點1處有水平和豎直方向上的位移約束，在節點3處有豎直方向上的位移約束。假定結構無阻尼，質量密度ρ＝2 700 kg／m3，桿件截面面積為A＝0．001 m2，令E＝5×1010Pa，桿件單元1－7的彈性模量分別為（0．6，0．6，0．7，0．8，0．7，0．8，0．9）E。

圖1 桁架結構示意圖Fig．1 Figure of the trussmodel

為了進行設計階段的分析，需要建立桁架結構名義上的有限元模型。名義模型是對結構進行設計時采用的理想模型，它不是實際的結構。為了模擬模型誤差對結構反應的影響，所選名義模型可與實際結構明顯不同。所選名義模型一：各桿件單元的彈性模量均取0．5E；名義模型二：各桿件單元的彈性模量均取0．8 E；名義模型三：各桿件單元的彈性模量均取E。三個名義模型的截面面積為A，質量密度為ρ，無阻尼。

下面主要討論利用桁架結構在服役期間的振動反應測試數據，考慮結構模型參數及模型誤差的不確定性，對結構的可靠度進行更新。

3.1 測點處自由度的可靠度更新

假定在該桁架結構的第2節點作用有動荷載B sin（20πt），其中B～N（40 kN，5 kN），B的各樣本相互獨立，時間間隔Δt＝0．01 s，持續時間為10 s。令位移界限值b＝16 mm，計算該桁架結構在以下三種情況下第2自由度位移的失效概率：

（1）假定彈性模量為確定值，僅考慮荷載的隨機性。

利用Monte-Carlo法，生成1 000個樣本，計算得實際結構、名義模型一、名義模型二、名義模型三的失效概率見表1。名義模型一各桿件的軸向剛度比實際結構各桿件的軸向剛度小，失效概率比實際結構的失效概率大；名義模型三各桿件的軸向剛度比實際結構各桿件的軸向剛度大，失效概率比實際結構的失效概率小；名義模型二的失效概率與實際結構的失效概率比較接近，但偏小。

（2）考慮彈性模量的先驗分布及荷載的隨機性。

假定桁架結構模型各桿件的彈性模量相等，且其先驗分布為正態分布，均值為0．7 E，變異系數為0．2。利用式（7），生成1 000個樣本，計算得更新前模型的失效概率見表1，與實際的失效概率相比偏大。由于模型參數先驗分布的選取依賴于工程經驗，故應通過測試數據對其更新后再用于計算。

表1 桁架結構模型第2自由度位移的失效概率Tab.1 Displacement failure probabilities of the 2nd DOF of the trussmodel

（3）利用彈性模量的后驗分布及荷載的隨機性。假定對該桁架結構在服役過程中第2自由度的位移進行了測試。設此時荷載為B sin（20πt），B＝30 kN，時間間隔Δt＝0．01 s，持續時間為10 s，所測得結構反應為模型計算反應加上10%均方差的高斯噪聲（見圖2）。

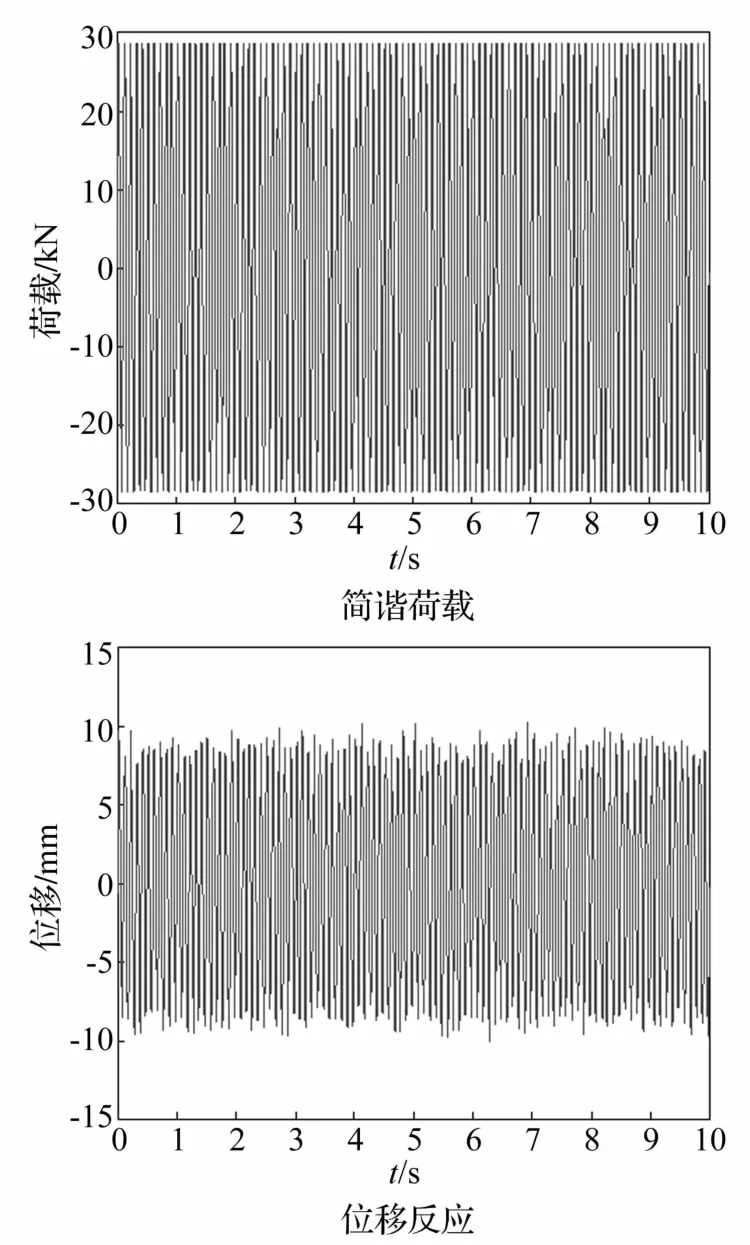
圖2 測試所得結構所受荷載及位移反應Fig．2 Tested loading and displacement histories of the truss

若令更新后桁架結構模型各桿件的彈性模量不等，則待識別的模型參數為7個，此種情況為不可識別問題。因此令桁架結構模型各桿件的彈性模量相等，利用貝葉斯參數識別方法，根據式（4）識別得到彈性模量的最有可能值為3．820×1010Pa（0．76 E），標準差為3．733×109Pa，變異系數為0．07。模型誤差標準差的最有可能值為20 mm。彈性模量更新前后的概率密度函數見圖3，彈性模量更新后變異系數減小，更新效果顯著。

圖3 彈性模量更新前后的概率密度函數Fig．3 Prior and posterior probability density function curves of elastic modulus

利用模型參數的更新分布生成100個樣本，利用這些樣本統計得到結構模型的自振頻率的均值及方差。各階頻率的均值加減三倍標準差的范圍見表2，可以看出實際結構的各階自振頻率均位于對應的范圍內。

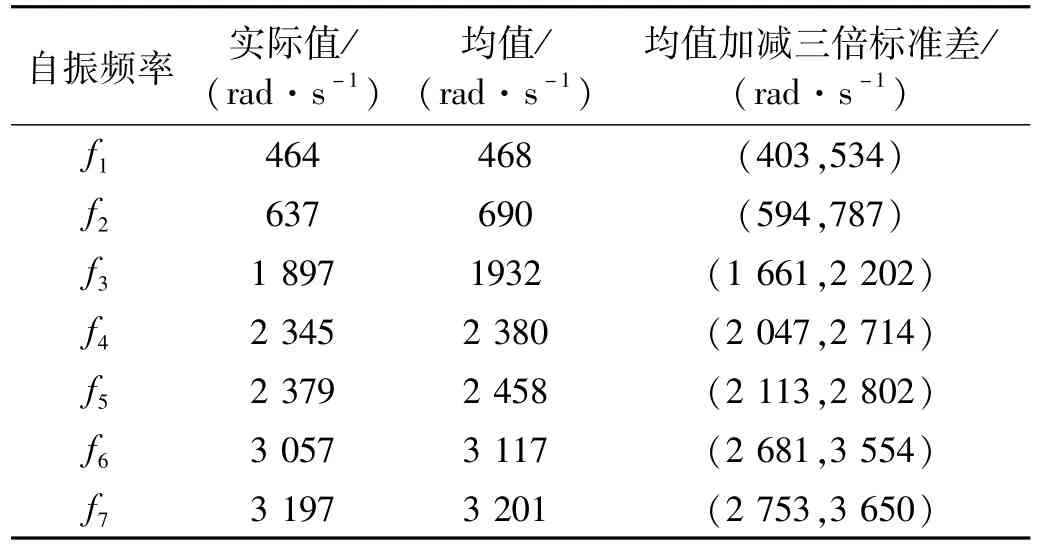
表2 桁架結構模型更新后的自振頻率范圍Tab.2 Natural frequency intervals of the updated trussmodel

根據模態保證準則（MAC）［15］，兩個振型向量u和v之間的MAC可以表示為

MAC的范圍為0～1，MAC越大，兩個振型的一致性越高。模型更新后取最有可能值時的振型與實際振型之間的MAC見圖4，可以看出模型更新后取最有可能值時的前三階振型與相應的前三階實際振型之間的MAC接近于1，一致性很好，后四階振型的一致性比前三階振型略差。

利用式（9），生成1 000個樣本，計算得更新后的失效概率見表1，其與實際的失效概率比較接近，并且偏于保守。從表1中的失效概率可以看出，無論采用哪個名義模型，只要利用結構在服役期間的反應數據對模型參數進行更新，都可以得到與實際失效概率吻合較好的結果。

從確定性的模型參數，到考慮模型參數的先驗分布，再到考慮模型參數的更新分布，反應了對模型不確定性認識水平的逐步提高。

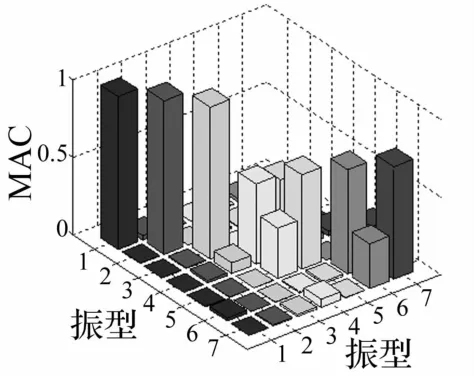
圖4 更新后振型與實際振型之間的MACFig．4 MAC between the updated and actualmode shape

3.2 未測試自由度的可靠度更新

若利用測得的第2自由度的位移反應，對其它自由度的位移失效概率進行更新，計算結果見表3。若在同樣的荷載下僅測試得第3自由度的位移反應（模型計算反應加10%均方差的高斯噪聲），對其它自由度的位移失效概率進行更新，計算結果見表4。

結果表明，未測試自由度的更新失效概率與相應的實際失效概率可能相差較大。這是因為利用測試數據得到的模型參數最有可能值是利用測試自由度的反應誤差最小得到的，而由更新的模型參數得到的未測試自由度的反應則可能與實際反應相差較大。若未測試自由度的反應小于測試自由度處的反應，則其更新失效概率小于實際失效概率，偏于不安全；若未測試自由度的反應大于測試自由度處的反應，則其更新失效概率大于實際失效概率，偏于保守。

表3 測得第2自由度反應時的位移失效概率Tab.3 Displacement failure probabilities with known tested displacements of the 2nd DOF

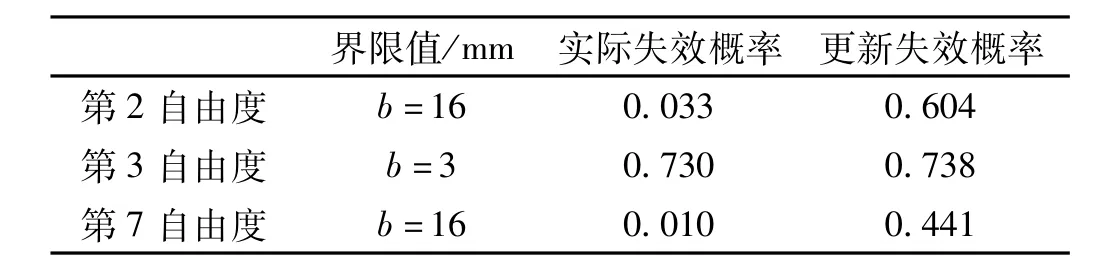
表4 測得第3自由度反應時的位移失效概率Tab.4 Disp lacement failure probabilities with known tested disp lacements of the 3rd DOF

3.3 利用多個自由度反應的可靠度更新

若同時測得第2和第7自由度的位移反應，利用這兩個自由度的反應識別得到彈性模量的最有可能值為3．824×1010Pa（0．76 E），標準差為3．742×109Pa，變異系數為0．10，模型誤差標準差的最有可能值為28 mm。此時彈性模量的標準差、模型誤差標準差的最有可能值，比僅利用第2自由度反應得到的值略有增大。

利用模型參數的更新分布生成100個樣本，利用這些樣本統計得到結構模型自振頻率的均值及方差。各階頻率的均值加減三倍標準差的范圍，比僅利用第2自由度反應得到的范圍擴大。彈性模量改變，剛度矩陣線性變化，模型更新后取最有可能值時的振型與實際振型之間的MAC值與圖4各值相同。由于模型假定各桿件的彈性模量相等，與實際結構不同，無論彈性模量取何值，都得不到與實際結構各階振型都有很好一致性的振型。

利用模型參數的更新分布得第2和第7自由度的更新失效概率見表5。可以看到，第2和第7自由度的更新失效概率與實際失效概率比較接近，并且偏于保守。

表5 測得第2和第7自由度反應時的位移失效概率Tab.5 Displacement failure probabilities with known tested disp lacements of the 2nd and 7th DOFs

若同時測得第2、第3、第7自由度的位移反應，利用這三個自由度的反應對失效概率進行更新。此時彈性模量的標準差、模型誤差標準差的最有可能值繼續增大，模型更新后各階自振頻率的均值加減三倍標準差的范圍擴大，各階振型不變。此時計算所得的更新失效概率見表6，可以看到，第2和第7自由度的更新失效概率與實際失效概率比較接近，并且偏于保守；由于各自由度的反應相差較大，第3自由度的更新失效概率與實際失效概率相差較大。因此，增加測試自由度數不一定提高失效概率的修正效果。

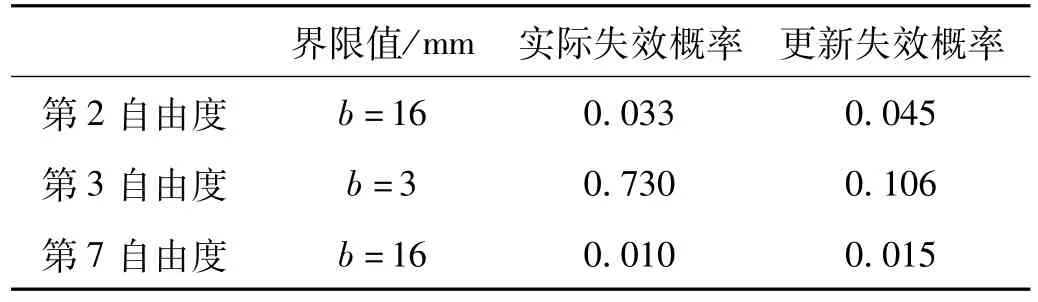
表6 測得第2、第3、第7自由度反應時的位移失效概率Tab.6 Disp lacement failure probabilitieswith known tested displacements of the 2nd，3rd and 7th DOFs

4 結 論

設計階段所采用的名義上的有限元模型不是實際的結構，也不能反映實際結構在服役過程中的損傷退化，故應考慮模型誤差對結構可靠度的影響。對結構進行健康監測，利用其在服役期間的振動反應數據及貝葉斯參數識別方法，可更新結構的可靠度，更準確的評估結構的安全性。

以某桁架結構為例，利用其在服役期間所得振動反應數據及貝葉斯參數識別方法，計算其在未來隨機荷載作用下的動力可靠度。結果表明：

（1）利用結構在服役期間某自由度的反應數據對模型參數進行更新，無論采用的確定性名義模型的參數取值大小，在測試自由度處都可以得到與實際結構失效概率吻合較好的結果。

（2）在未測試自由度處的更新失效概率與相應的實際失效概率可能相差較大：若未測試自由度的反應小于測試自由度處的反應，則其更新失效概率小于實際失效概率，偏于不安全；若未測試自由度處的反應大于測試自由度處的反應，則其更新失效概率大于實際失效概率，偏于保守。

（3）由于各自由度的反應可能相差較大，增加測點數不一定改善失效概率的更新效果。

因此，建議對于桁架結構，在實際工程中，可有針對性的選擇結構的可能失效部位進行動力響應測試，并利用該測試數據對該位置的可靠度進行更新。

［1］Beck JL，Katafygiotis L S．Updatingmodels and their uncertainties．I：Bayesian statistical framework［J］．Journal ofEngineering Mechanics，1998，124（4）：455－461．

［2］Beck JL．Bayesian system identification based on probability logic［J］．Structural Control and Health Monitoring，2010，17（7）：825－847．

［3］Papadimitriou C，Beck JL，Katafygiotis L S．Updating robust reliability using structural test data［J］．Probabilistic Engineering Mechanics，2001，16（2）：103－113．

［4］Soyoz S，Feng MQ，Shinozuka M．Structural reliability estimation with vibration-based identified parameters［J］．ASCE Journal of Engineering Mechanics，2010，136（1）：100－106．

［5］Katafygiots L S，Yuen K V．Bayesian spectral density approach for modal updating using ambient data［J］．Earthquake Engineering and Structural dynamics，2001，30（8）：1103－1123．

［6］Au SK．Fast Bayesian FFTmethod for ambientmodal identification with separated modes［J］．ASCE Journal of Engineering Mechanics，2011，137（3）：214－226．

［7］Au SK，Zhang F L．Ambientmodal identification of a primary-secondary structure by Fast Bayesian FFT method［J］．Mechanical Systems and Signal Processing，2012，28（4）：280－296．

［8］易偉建，吳高烈，徐麗．模態參數不確定分析的貝葉斯方法研究［J］．計算力學學報，2006，23（6）：700－705．

YIWei-jian，WUGao-lie，XU Li．A study on the uncertainty ofmodel parameters by Bayesian method［J］．Chinese Journal of Computational Mechanics，2006，23（6）：700－705．

［9］Au SK，Zhang F L．On assessing the posteriormode shape uncertainty in ambientmodal identification［J］．Probabilistic Engineering Mechanics，2011，26（3）：427－434．

［10］Liu P，Au SK．Bayesian parameter identification of hysteretic behavior of composite walls［J］．Probabilistic Engineering Mechanics，2013，34（10）：101－109．

［11］Yuen K V，Beck J L．Updating properties of nonlinear dynamical systems with uncertain input［J］．ASCE Journal of Engineering Mechanics，2003，129（1）：9－20．

［12］易偉建，周云，李浩．基于貝葉斯統計推斷的框架結構損傷診斷研究［J］．工程力學，2009，26（5）：121－129．

YIWei-jian，ZHOU Yun，LI Hao．Damage assessment research on frame structure based on Bayesian statistical inference［J］．Engineering Mechanics，2009，26（5）：121－129．

［13］Sohn H，Law K H．A Bayesian probabilistic approach for structure damage detection［J］．Earthquake Engineering and Structural dynamics，1997，26（12）：1259－1281．

［14］Papadimitriou C，Beck JL，Katafygiotis L S．Asymptotic expansions for reliability and moments of uncertain systems［J］．ASCE Journal of Engineering Mechanics，1997，123（12）：1219－1229．

［15］?ahin A，Bayraktar A，?zcan D M，et al．Dynamic field test，system identification，and modal validation of an RC Minaret：Preprocessing and postprocessing the wind-induced ambient vibration data［J］．ASCE Journal of Performance of Constructed Facilities，2011，25（4）：336－356．

Structural dynam ic reliability updating method based on Bayesian theorem

LIU Pei1，2
（1．School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China；2．Beijing's Key Laboratory of StructuralWind Engineering and Urban Wind Environment，Beijing 100044，China）

An approach based on Bayesian theorem and structural vibration test data was presented for reliability updating．The approach takes account of uncertainties of the excitation，structuralmodel and its parameters．Structural model parameters were identified based on the vibration test data and Bayesian parameter identification．According to Laplace asymptotic approximation，the dynamic reliability estimated purely in the light of design conditionswas updated．The reliabilities of a truss structure subjected to dynamic random loading were calculated for three cases．Only the uncertainty of the loading was considered for the first case．The uncertainties of the loading and the prior probability distribution ofmodel parameters were considered for the second case．The uncertainties of the loading and the updated probability distribution ofmodel parameterswere considered for the third case．Natural frequencies andmode shapes of the actual structure and the updatedmodelwere compared．Discussions about the updated reliabilitiesweremade．The results show that the updated failure probability of the tested DOF agrees better with the actual value compared with that by deterministic nominal models．The updated failure probability of untested DOFs may deviate from the actual values．Increasing tested DOFsmay have no effect on the updated failure probability．

Bayesian theorem；dynamic reliability；parameter identification；failure probability；updated probability distribution

TU311

A

10．13465／j．cnki．jvs．2015．12．006

中央高校基本科研業務費（2014JBM100）資助項目

2014－02－19 修改稿收到日期：2014－05－27

劉佩 女，博士，副教授，1982年生