三質體振動機動力學參數對其性能的影響分析

趙春雨，趙乾斌，賀 斌，聞邦椿

（東北大學機械工程與自動化學院，沈陽 110819）

三質體振動機動力學參數對其性能的影響分析

趙春雨，趙乾斌，賀 斌，聞邦椿

（東北大學機械工程與自動化學院，沈陽 110819）

提出了工作質體無量綱特征幅值、特征幅值放大倍數、最大參振物料系數、隔振架與基礎之間的力傳遞系數、同步能力系數和臨界隔振頻率比作為描述三質體振動機的性能指標。通過數值計算，研究了系統動力學參數對振動機各性能指標的影響規律。當工作質體工作于超共振態時，特征幅值和力傳遞系數隨隔振頻率增加而減小。當隔振頻率比相同且大于臨界隔振頻率比時，隨工作質體與隔振質體質量比的減小，初始特征幅值和最大力傳遞系數增大，特征幅值放大倍數和最大參振物料系數略有減小，即較小的工作質體與隔振質體質量比，有利于提高振動機的綜合性能指標。振動激勵角越小，系統同步能力系數越大。當支撐剛體作為物料箱時，同步能力系數隨工作質體與激振器安裝剛體的質量比的增加而增大。系統結構能夠滿足兩激振器自同步運行的穩定性要求，計算機仿真結果驗證了理論研究的正確性。

振動系統；隔振；自同步；穩定性

早在1948年，列寧格勒Mekhanobr學院研究人員Pliss和Abramovich發現了安裝同一剛性機架上兩個偏心轉子的自同步現象；1950年，瑞典發明家Signul在瑞典申請了最簡單自同步振動機專利，并聲明瑞典于1946發現了雙偏心轉子的自同步現象［1］。1953年，前蘇聯學者Blekhman利用小參數Poincare-Lyapunov方法與運動穩定性理論，從物理上解釋了兩偏心轉子的自同步現象，并給出完整的數學證明，由此發展成振動系統中偏心轉子自同步分析的基于直接運動分離的小參數平均法［2］。在20世紀70年代始，我國學者聞邦椿院士將雙偏心轉子的運動微分方程合并為相位差擾動參數的一個微分方程，簡化了系統的穩定性分析，發明了一系列的振動機械，創建了振動利用工程新學科［3－5］。目前，自同步振動機械廣泛應用于工業生產部門，如：振動篩、振動給料機、振動拋砂機、振動輸運機等。但是，振動機對基礎激勵所帶來的負作用一直是振動機械應用未能解決的難題。盡管已提出了許多隔振措施，如雙質體與多質體隔振、反共振等［6］，振動機對基礎的作用仍不能完全抵消，尤其是大型振動機械對地基激勵較大，甚至引起附近建筑物振動，嚴重影響周圍環境。另外，振動機振動幅值不能隨給料量增加而增加，影響振動機的生產率。

1 系統的動力學模型

1.1 系統運動微分方程

圖1提出了具隔振的三質體振動系統的動力學模型，由激振器安裝剛體m1、支撐剛體m2、隔振質體Mr以及兩偏心轉子m01和m02組成。質體m1在水平x和y方向分別通過軟彈簧與支撐剛體m2相連接，支撐剛體m2通過硬彈簧在z方向與隔振質體Mr相連接，且在x和y方向被固定，隔振剛體Mr被支撐在z方向的彈性基礎上（見圖1）。兩偏心轉子m01和m02沿垂直軸對稱地安裝在物料箱剛體m01內，分別由感應電動機1和感應電機2驅動。旋轉中心o1和o2過振動方向軸，關于質體m1的質心對稱，旋轉軸與振動方向軸成δ角，稱為振動激勵角，旋轉平面關于水平面xoy對稱且與xoy平面成δ角。俯視兩偏心轉子同向回轉（逆時針），（見圖1（b））。

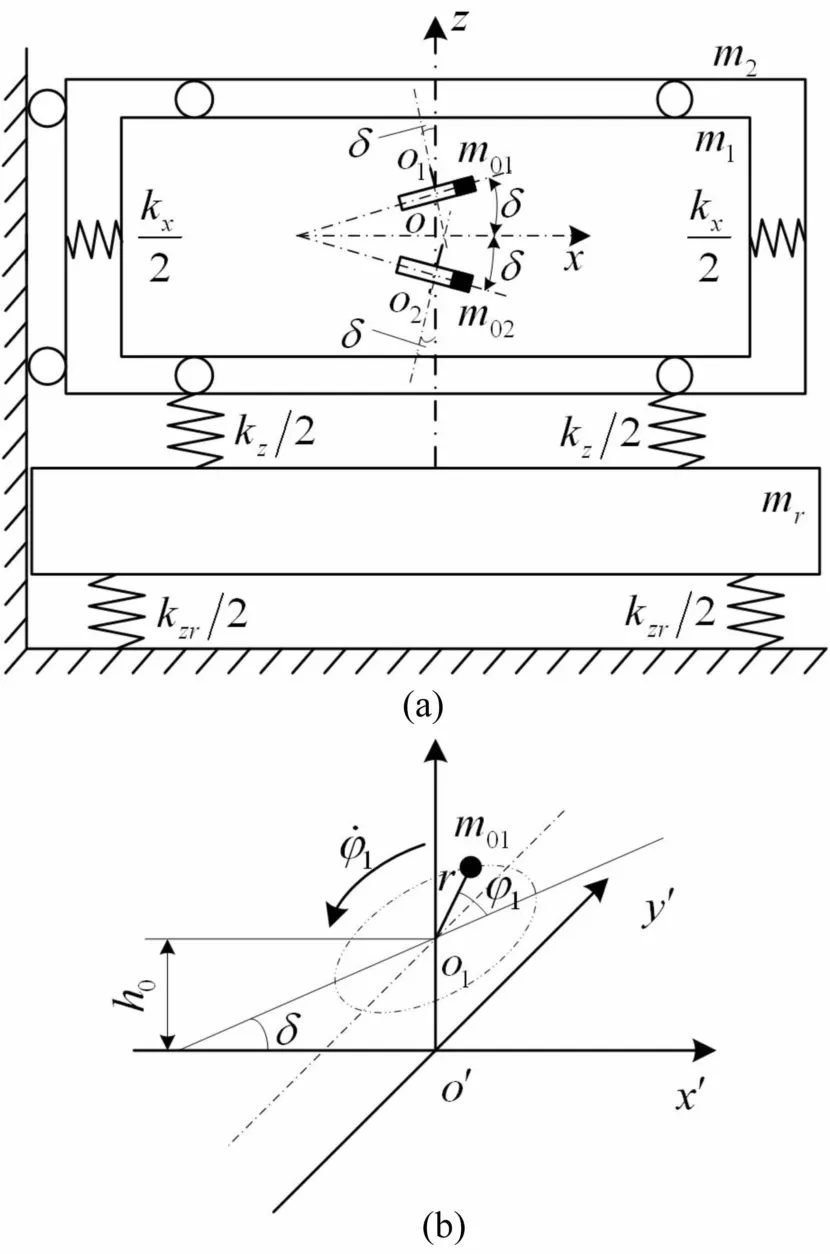
圖1 雙機驅動三質體振動機的動力學模型Fig．1 Dynamicmodel of a three-mass vibratingmachine with dual-motor drives

式中：M1為激振器安裝剛體的參振質量，M1＝m1+m01+m02；M2為振動工作質體的質量；kβ和fβ分別為振動系統在相應方向的剛度與阻尼β＝x，y，z，zr；Tei、J0i和fdi分別為電機i（i＝1，2）電磁轉矩、轉子轉動慣量與阻尼系數；r為偏心半徑。

1.2 兩偏心轉子的無量綱耦合方程

若設激振器的平均相位為φ，相位差為2α，平均角速度為ωm，平均角速度波動系數為ε1，相位差波動系數為ε2，則有［7－9］

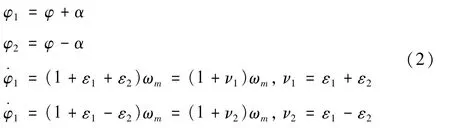
由于異步電動機轉速變化比較小，可以以激勵頻率為ωm求得振動系統的響應，且穩態運行時可忽略角加速度對激勵的影響。即式（1）前4個方程可以簡化為：

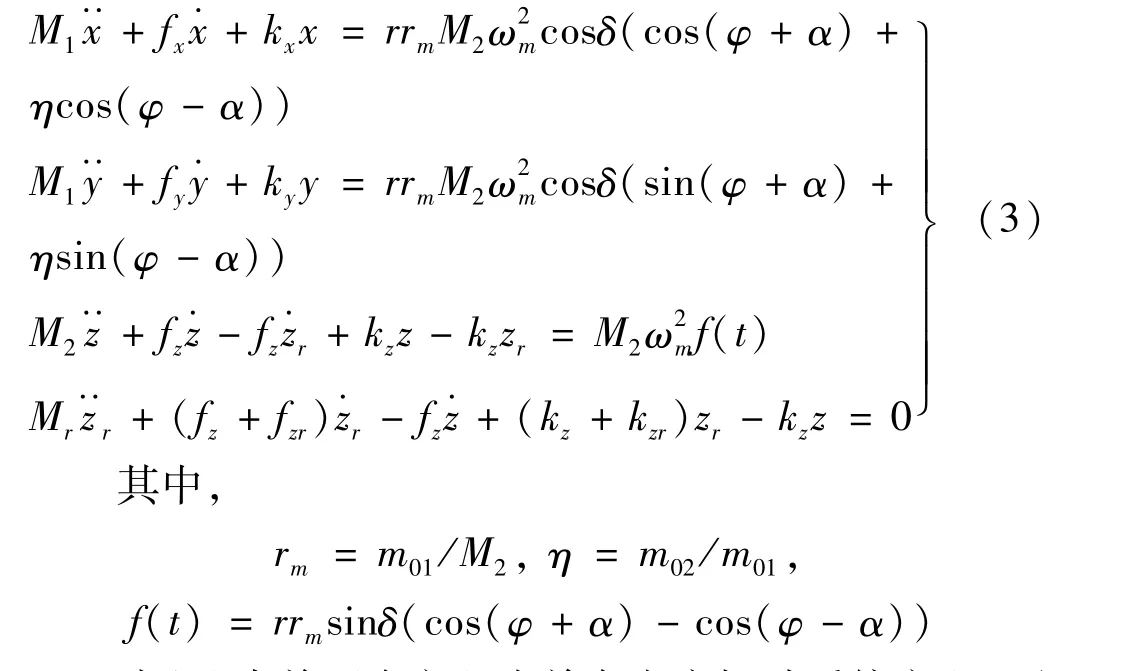
式（3）中前兩個方程為單自由度振動系統方程，可以直接寫出其穩態解。后兩個方程為兩自由度耦合系統，對其在初始條件下進行拉氏變換，求得其傳遞函數為：

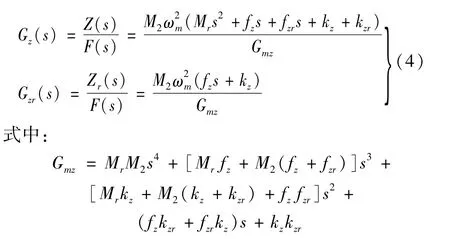
令s＝iωm，則可得到系統在z和zr的復頻域傳遞函數，并將分子分母同時除以kzkzr，經化簡整理成以下形式

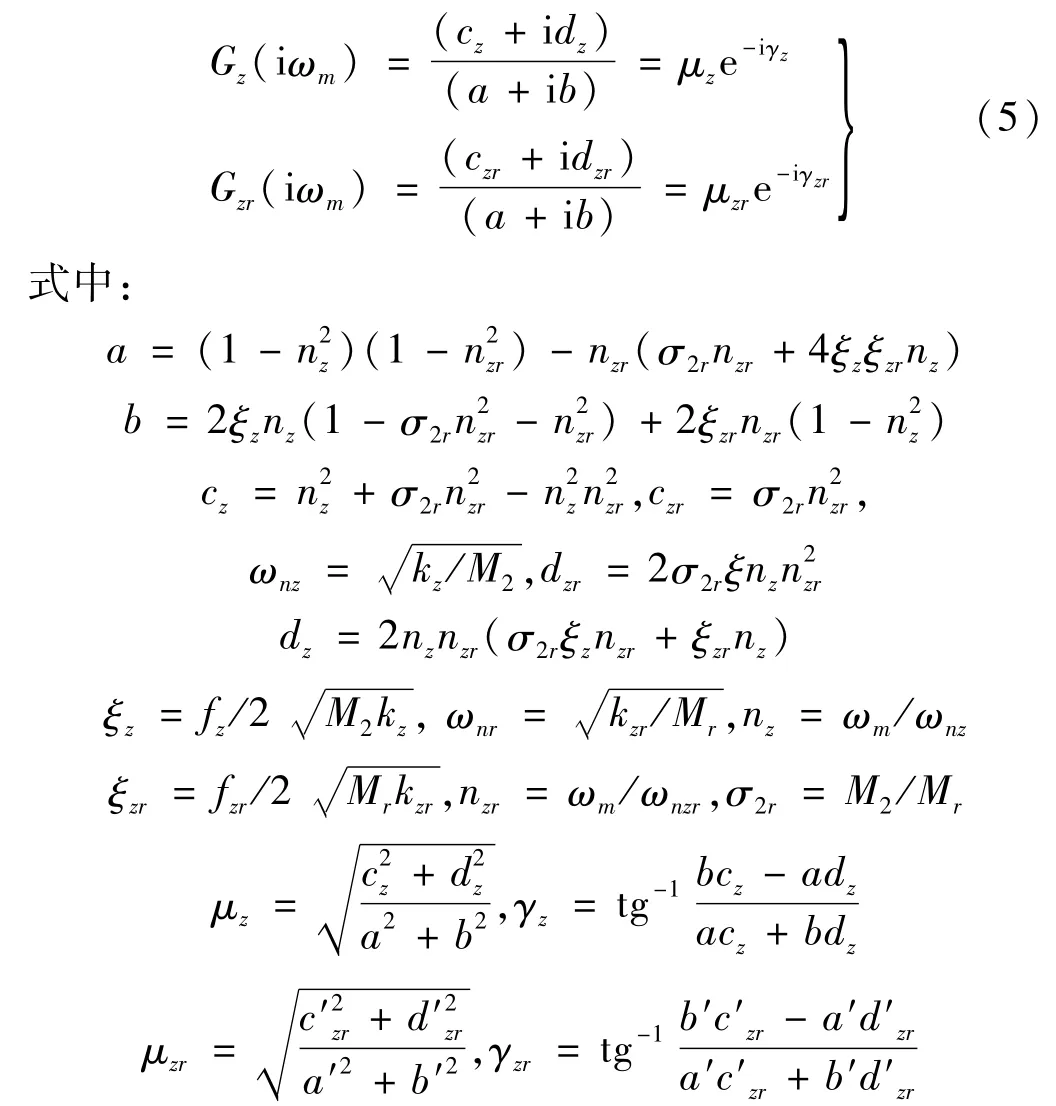
則利用式（5），可以直接寫式（3）在兩偏心轉子激勵下的振動穩態響應解為：

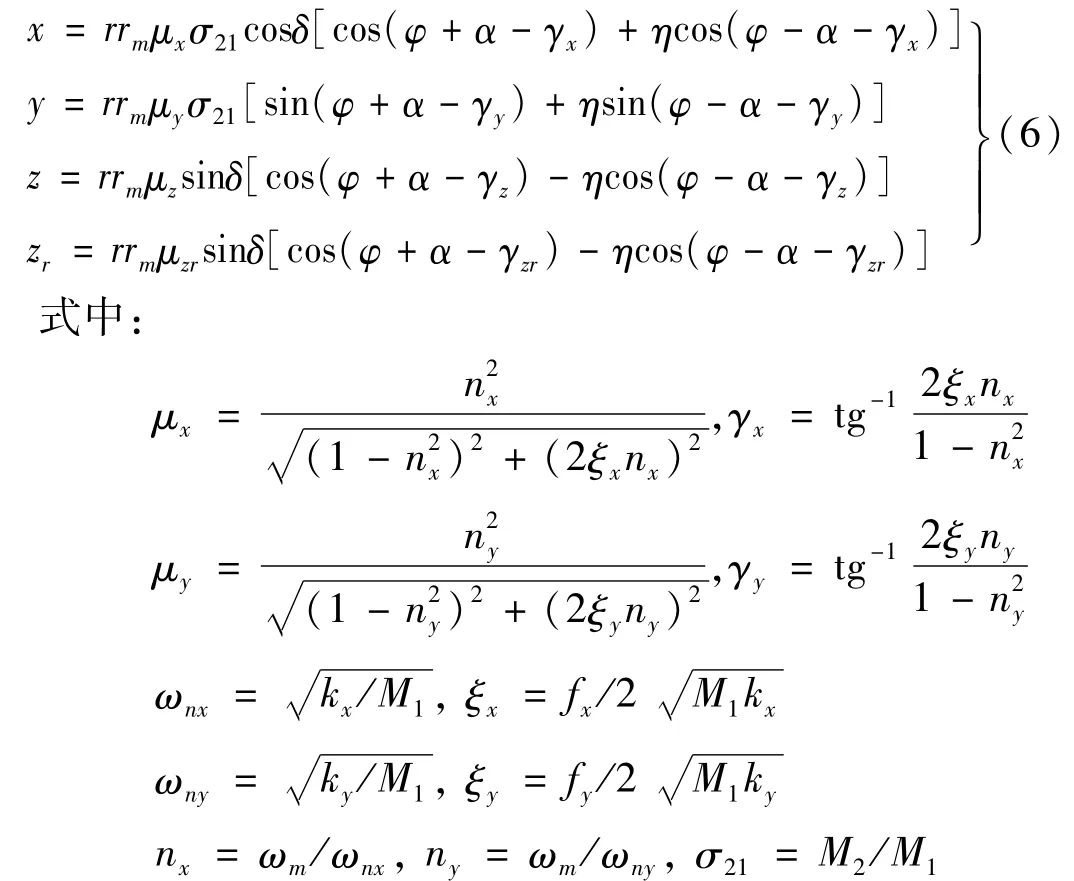
將式（6）中的x，y和z對t求導二次，得·x·、·y·和·z·， 考慮式（2），將其代入式（1）中兩偏心轉子的運動微分方程，并在0～2π上積分，忽略v1和v2的高階項，得到單周期平均微分方程為

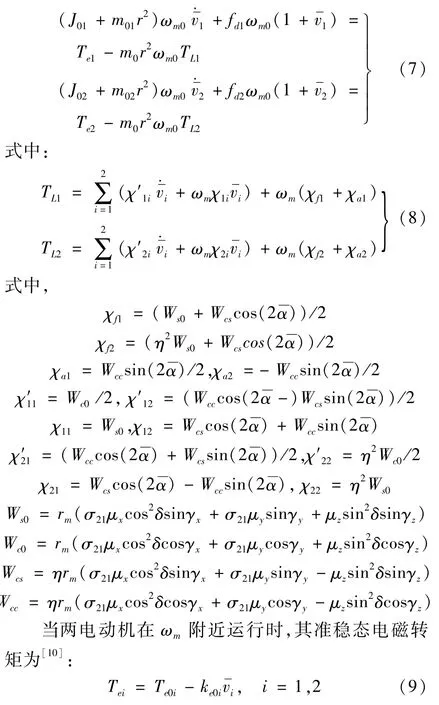
式中：Tei和ke0i分別為電機i在角速度為ωm時的電磁轉矩和角速度剛度系數。

由于電動機轉子的轉動慣量遠小偏心塊的轉動慣量，所以式（6）為Joi可以忽略，將式（8）和式（9）代入式（7），并將各方程兩邊同除以m01r2（標準轉子）后寫成矩陣形式，得

式（10）稱為兩激振器的無量綱耦合方程。其中，A為兩激振器的慣性耦合矩陣；B為兩電動機的角速度剛度耦合矩陣；u表示兩電動機的負載耦合關系。

2 兩激振器的自同步

2.1 兩激振器實現同步的條件

若系統能實現兩偏心轉子的同步，則在單周期內兩偏心轉子的角速度瞬時波動系數的均值為0，即式（10）中u＝0，整理可得：式中：Tu為標準偏心轉子的動能；TR1和TR2兩偏心子的剩余電磁轉矩，

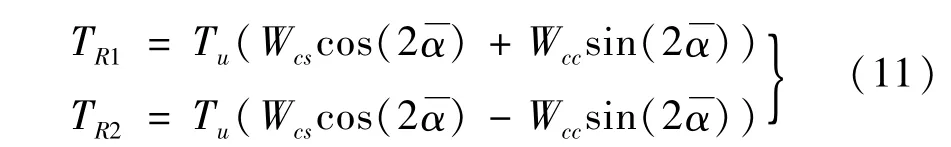
由式（11）可知，當Wcc＞0時，兩激振器的廣義動態對稱角為0；當Wcc＜0時，兩激振器的廣義動態對稱角為π；廣義同步力矩為TS＝TuWcc，則由式（11）兩式相差可得：

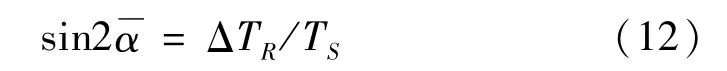
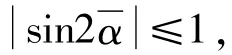
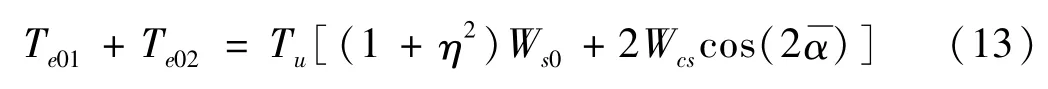
式（13）右側表示振動系統作用在兩個電動機上的負載轉矩，而兩電機電動機電磁剩余轉矩差永遠小于振動系統作用在在兩個電動機上的負載轉矩的一半。因此，在此定義振動系統的同步能力系數（也稱廣義動態對稱系數）為：

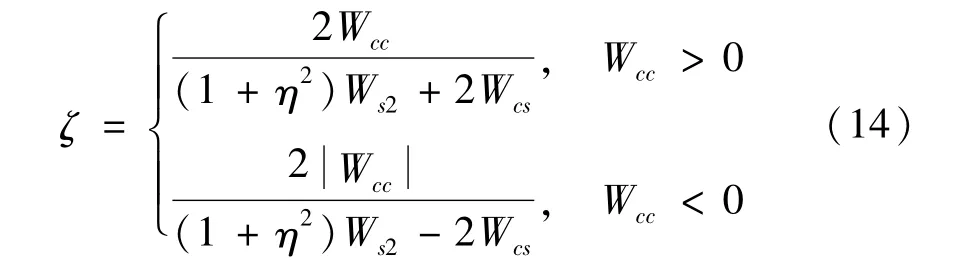
2.2 兩激振器同步運行的穩定性

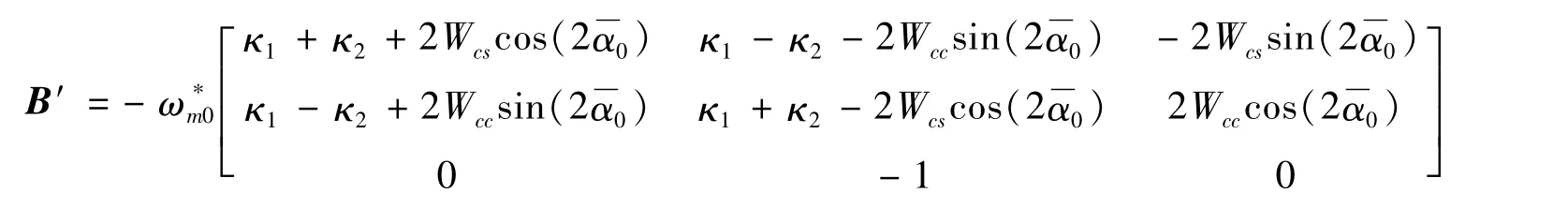
通過C＝A′－1B′求出矩陣C。由det（C－λI）＝0得矩陣C的特征方程：

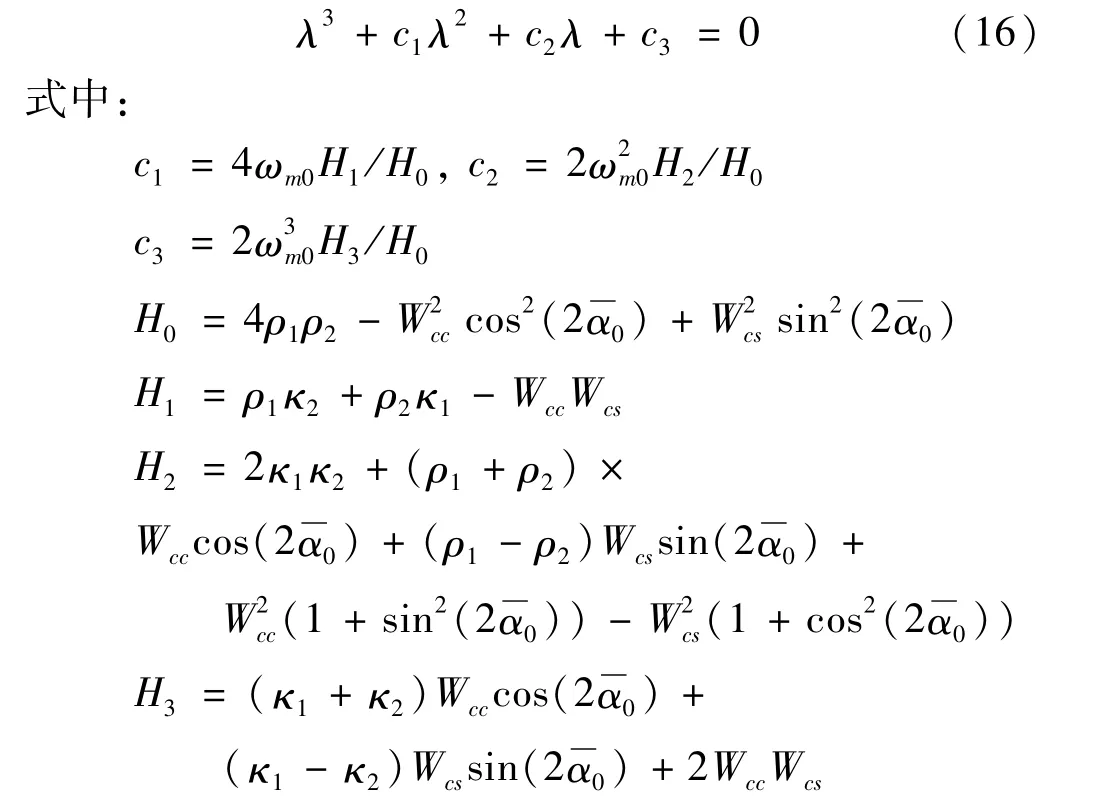
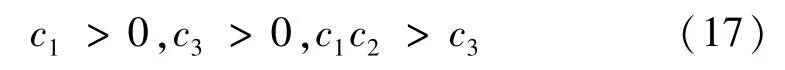
由Routh-Hurwitz準則可知，當矩陣C的特征方程（16）參數滿足［11］時，平凡解z＝0是穩定的。對于振動機械，由于系統結構總是滿足于H0＞0，所以式（17）可進一步寫成

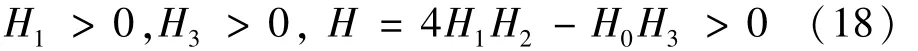
3 系統參數計算結果與討論

這里提出的振動系統結構要解決如下三個問題：①振動系統隔振問題；②增加兩激振器同步能力；③保證系統同步運行的穩定性。在此通過數值計算，討論系統參數對這三個問題的影響規律。數值計算僅研究兩偏心轉子質量相等的情況，即η＝1。

3.1 系統對基礎的力傳遞系數

采用隔振架減小振動系統工作過程對地基的動態激勵，同時保證工作質體要有足夠的工作振幅。單偏心轉子所激勵起的系統振動引起隔振體對地基作用力的幅值可以表示為：

將隔振架對地基作用力與z方向單偏心轉子激勵的幅值比定義為系統對基礎的力傳遞系數。考慮到式（5）和式（6）各無量綱系數定義，得：

圖2給出了工作質體與隔振質體質量比σ2r為0．1、1和5時系統對基礎的力傳遞系數隨兩個頻率比的變化規律。由圖可知，當工作質體工作于超共振態時（nz＞1），力傳遞系數隨隔振頻率比增大而迅速減小，而且σ2r越大，力傳遞系數趨近零的速度越快。當工作質體工作于亞共振態時（nz＜1），一個確定的σ2r對應一個隔振頻率比值nzrc，稱為臨界隔振頻率比，當nzr＞nzrc時，力傳遞系數隨著隔振架頻率比增大逐漸趨近于零；σ2r越大，nzrc越小，力傳遞系數趨近零的速度越快。當nzr向零趨近時，力傳遞系數隨nz在亞共振區向1接近逐漸增大；但當nzr從0向nzrc增大時，對應每個nz值的力傳遞系數會出現一個最大值，此值的最大值對應的nzr值隨σ2r增大而減小。

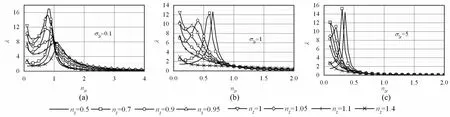
圖2 系統的力傳遞系數隨系統參數的變化Fig．2 Variation of the force transfer coefficientwith the system parameters

式（6）中μz為表征了單個偏心轉子激勵起的工作質體幅值隨系統動力學參數的變化規律，在此定義為工作質體的無量綱特征幅值，簡稱特征幅值。圖3給出特征幅值隨系統動力學參數變化規律。比較圖中四種計算結果，可以將特征幅值隨工作質體工作頻率比變化分為兩個區間，第一區間nzr在小于nzrc到0區間，第二區間nzr大于nzrc。在第一區間，特征幅值隨著工作頻率比向1接近而增大，且變化規律比較復雜；在第二區間，特征幅值隨nzr增加逐漸趨近于恒定值，且對應最大特征幅值的工作質體頻率比略大于1，隨工作質體頻率比遠離此值，特征幅值迅速下降。隨σ2r增大，第一區逐漸減小，第二區逐漸消失。

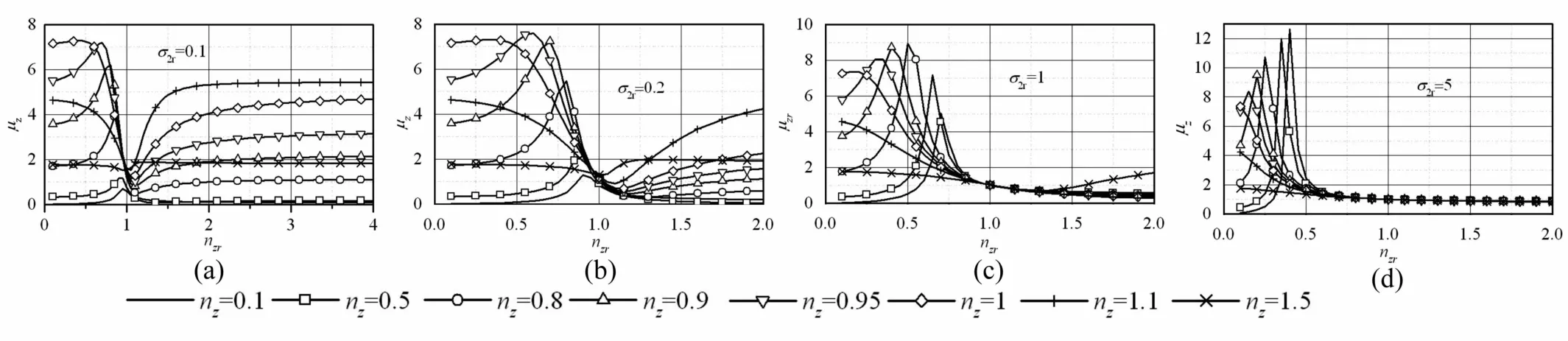
圖3 無量綱特征幅值隨系統參數變化Fig．3 Variation of the dimensionless characteristic amplitude with the system parameters

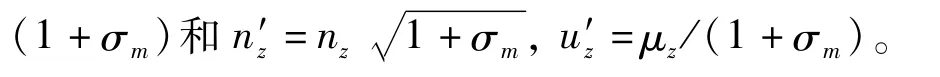
圖4和圖5給出了特定參數下特征幅值和力傳遞系數隨參振物料質量比的變化規律。依據圖2和圖3的數值計算結果，圖中（a）和（b）隔振頻率比選擇為3，而圖（c）為0．15。由圖4和圖5可見，振動系統動力學參數決定著振動機性能指標。表1給出了不同工況下性能參數數值計算結果。通過表1與圖4、5可以看出，特征振幅的初值，即空載特征振幅，隨工作質體工作頻率比在亞共振區向1接近而增大，但最大參振物料系數減小，特征幅值放大倍數減小，最大力傳遞系數增大。比較圖3、圖4中的（a）（b）與（c），表1的第1、2行與第3、4行，可以看出，當隔振頻率比小于臨界隔振頻率比時，力傳遞系數較大，不適合于此類振動系統。比較圖3和圖4中的（a）、（b）及表1中第1、第2行數據可以看出，在隔振頻率比相同且大于臨界隔振頻率比時，對應于工作質體在亞共區確定的頻率比，隨σ2r減小，初始特征幅值增大，特征幅值放大倍數略有減小，最大力傳遞系數略有增大，最大參振物料系數減小。綜合各性能指標可以看出，較小的σ2r值，有利于提高振動系統綜合性能指標。

3.2 系統的同步能力系數

由2．1節可知，當Wcc為正時，廣義動態對稱角0；當Wcc為負時，廣義動態對稱角π。由系統結構可以看出，當相差為0時，兩激振器在x和y方向的兩個激勵相互疊加，而z方向的激勵相互抵消；當相位差為π時，兩激振器在x和y方向的兩個激勵相互抵消，而z方向的激勵相互疊加。即系統有兩種運動選擇，質體m1在xy平面的橢圓運動或三質體在z方向的振動［12－13］。由Wcc表達式可見，若ωm0大于ωnx和ωny，則前兩項小于0；而b′c′z－a′d′z和a′c′z+b′d′z同號時，第三項為負，否則為正。如果設計時保證x和y兩個方向為過共振工作，z方向亞共振工作，系統的廣義動態對稱角為π，由Wcc表達式可以看出，系統三個運動都驅動兩偏心轉子的相位差向π接近。在此設定nx＝ny＝4，通過數值計算研究系統工作過程中同步能力系數隨系統參數的變化。

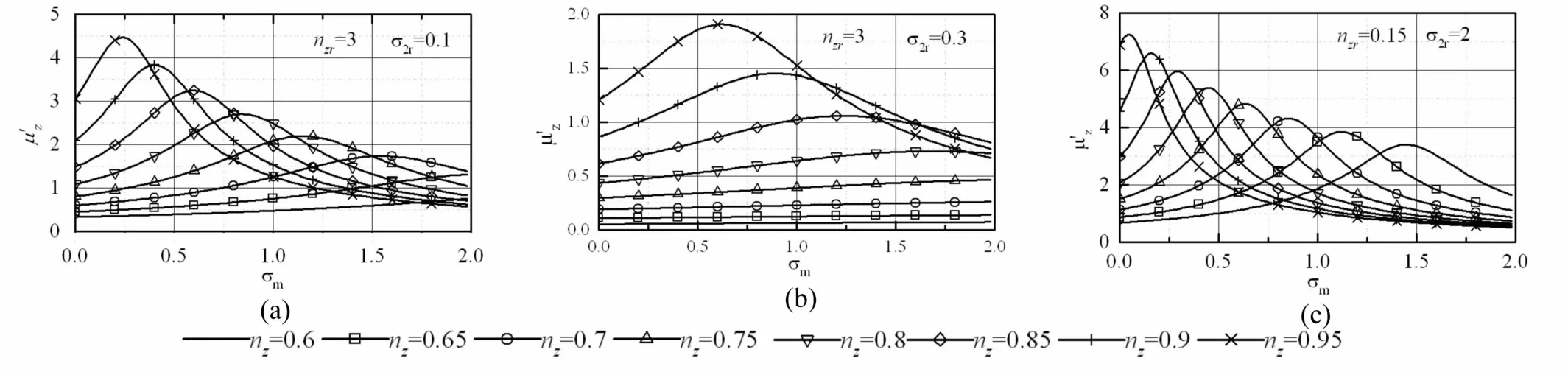
圖4 特征幅值隨參振物料質量比的變化Fig．4 Variation of the characteristic amplitude with the ratio of vibrationmaterial

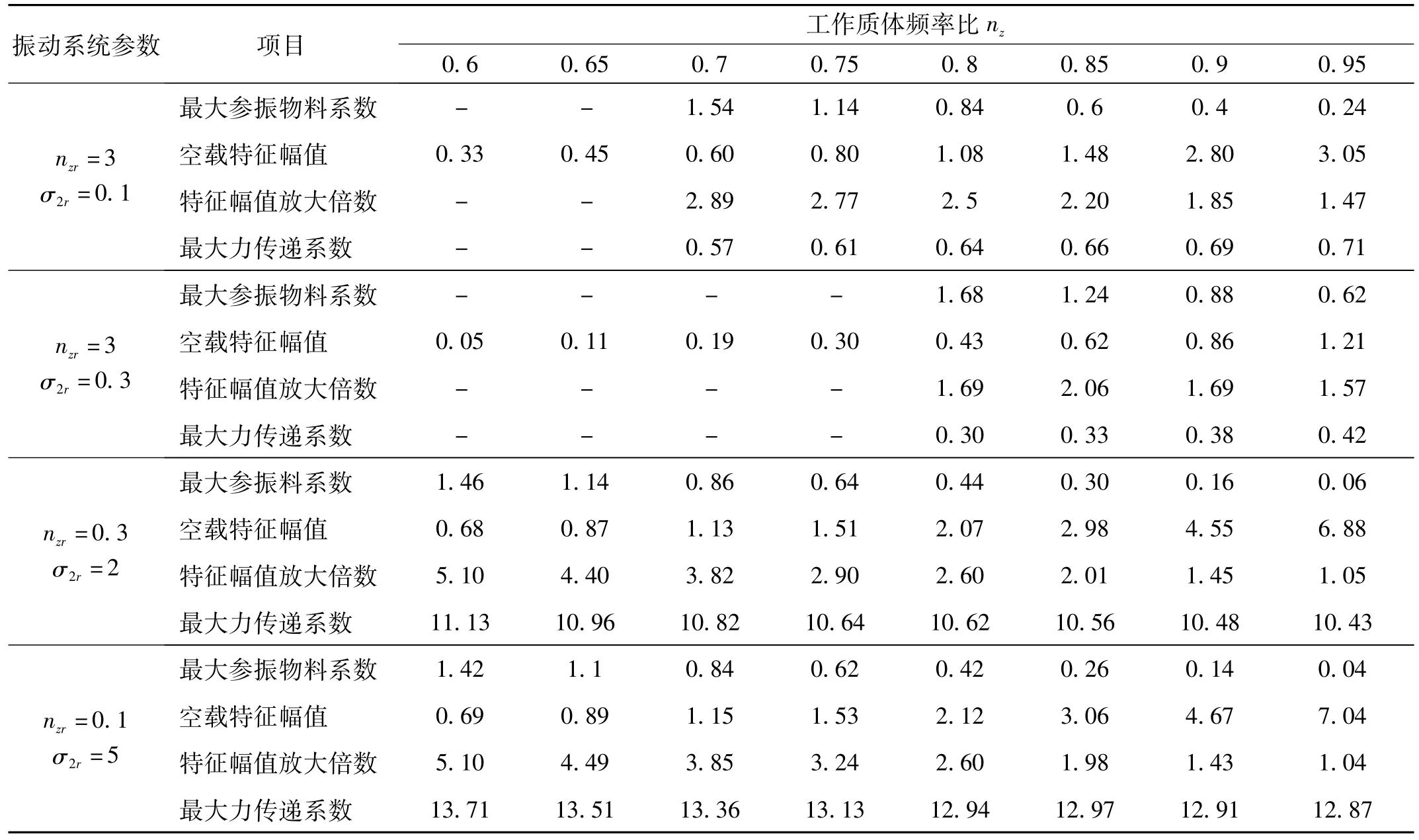
表1 不同給定參數下的振動系統特征參數Tab.1 Performance param eters of the vibrating system under different dynam ic param eters

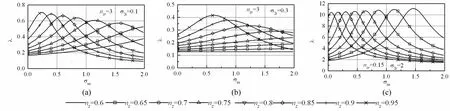
圖5 力傳遞系數隨參加物料質量比的變化Fig．5 Variation of the force transfer coefficientwith the ratio of vibration materials

圖6給出了兩種工況情況下同步能力系數的計算結果。將圖4與圖6比較可見，同步能力系數在特征幅值最大時達到最小值，而且當δ一定時，同步系數最小值受其它參數影響較小，其原因是Wcc中無量綱參數σ21隨參振物料系數的變化引起的。圖7給出了同能力系數最小值隨激勵角的變化規律，其中，圖7（a）物料箱為激振器安裝剛體m1，圖7（b）物料箱為支撐剛體m2。由圖可見，振動激勵角越小，最小同步能力系數越大。但為了獲得z方向的工作振幅，在保證系統具有足夠同步能力的基礎上，激勵角越接近于π／2越好。由式（14）可見，當兩偏心轉子相同時，同步能力系數分母僅與z方向振動相關（Wcc＜0），而分子與三個方向的振動都相關。當系統達到共振狀態時，同步能力系數最小，此時z方向對同步能力系數分子項影響為零，而分母項達到最大值。當質體m1做為物料箱時，參振質量直接加在m1上，增加了質體m1的質量，使得同步能力系數中σ21減小，而σ21初始值對同步能力系數影響不明顯，如圖（a）所示。當質體m2為物料箱時，物料增加m2的質量，使σ21增大，因此，σ21初值對同步能力系數影響較大，如圖（b）所示。當同步能力系數大于1時，系統可以實現振動同步傳動［12］，即可認為同步能力系數已達到足夠大。比較圖7（a）和（b）的計算結果可以發現，質體m2作為物料箱可以大大提高振動激勵角，增加系統有效激振力。

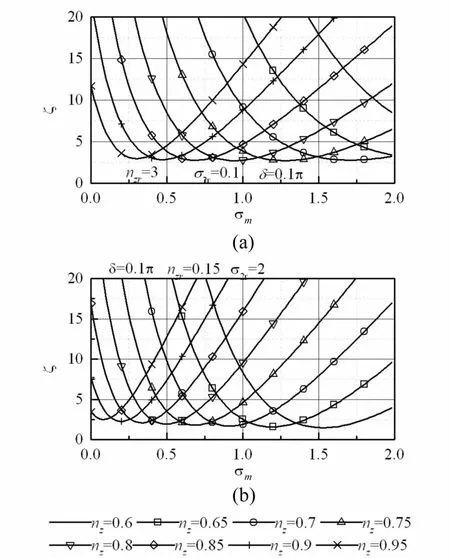
圖6 同步能力系數（σ21＝0．5）Fig．6 Coefficient of synchronization ability（σ21＝0．5）

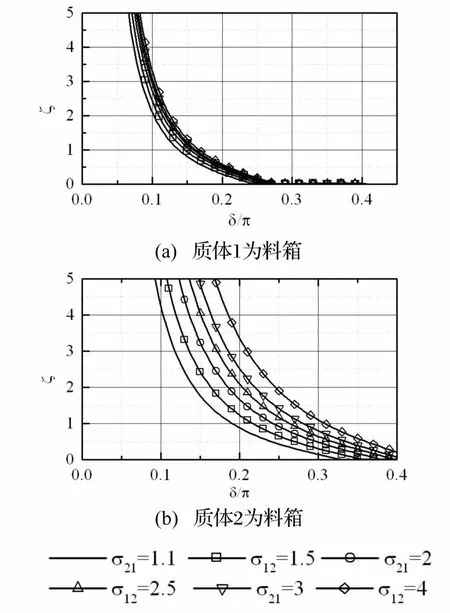
圖7 同步能力系數與隨偏心轉子激勵角的變化（nz＝0．8，σ2r＝0．1，nzr＝3）Fig．7 Variation of synchronization ability synchronization with the exciting angle of the unbalanced rotors（nz＝0．8，σ2r＝0．1，nzr＝3）

3.3 同步運行的穩定性

當系統結構參數滿足式（18）條件時，同步運行是穩定的。式（18）中H0、H1、H3和H均為無量綱結構參數的函數。設rm＝0．05，nz＝0．8，δ＝0．3π，其它參數與圖6（b）的參數相同。對振動系統工作過程的穩定性參數進行了計算，圖8為計算結果。由圖可見，系統工作過程中能夠保證各指標都大于0，即兩偏心轉子同步運行是穩定的。大量計算結果表明雙機驅動振動系統的結構總能夠保證兩偏心轉子同步運行的穩定性要求。

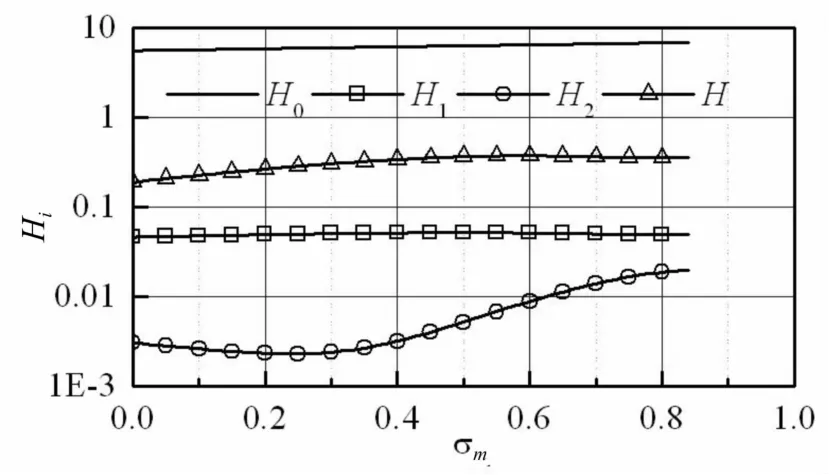
圖8 H0、H1、H2和H隨參振物料系數的變化Fig．8 Variations of H0－，H1－，H2－and H-values with the coefficient of vibration materials

4 計算機仿真結果

通過計算機仿真驗證上述理論分析結果。為了驗證同步系統同步能力，選擇不同的兩個電動機，且選擇m2為物料箱。設激振器安裝剛體m1＝900 kg，物料箱剛體m2＝1 600 kg，Mr＝2 500 kg，兩偏心轉子質量同為40 kg，偏心距r＝0．15 m，kz＝17 300 kN／m，kx＝k2＝200 kN／m，kr＝30 000 kN／m，fx＝fy＝1 080 N／（m·s－1），fz＝29 kN／（m／s），δ＝20°。系統的無量綱參數為：σ21＝2．8，σ2r＝0．1，ξi＝0．07（i＝x，y，z，zr），nz＝0．8，nzr＝3，nx＝ny＝4。

圖9為計算機仿真結果。由圖可知，系統啟動約4 s后，系統進入兩偏心轉子同步運行狀態，轉速為993．1 r／min，兩偏心轉子的穩態相位差為181．4°，x和y方向振幅接近0，而z方向振動幅值為1．66 mm，而隔振體也出現穩定的振幅0．04 mm。在9 s時，對偏心轉子2施加10°的相位差擾動，由于同步力矩的調節作用，兩偏心轉子轉速及相位差產生了波動，但在1．5 s后，系統又進行穩定運行狀態。由此可見，相位差π是穩定的。

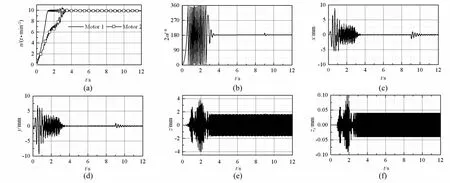
圖9 計算機仿真結果Fig．9 Results of computer simulation

5 結 論

（1）提出了一種新的兩偏心轉子驅動三質體亞共振振動機構，其中，工作質體由激振器安裝剛體和支撐剛體組成，可以實現振動幅值隨參振物料質量的增加而增大，推導出系統實現同步與同步穩定性運行的條件。提出了振動系統無量綱特征幅值、同步能力系數、無量綱特征幅值放大倍數、系統的力傳遞系數及臨界隔振頻率比衡量振動機性能指標。

（2）在振動系統空載情況下，當工作質體工作于超共振態時或隔振頻率比大于臨界隔振頻率比時，力的傳遞系數隨隔振頻率比增大而減小，且隨隔振質量比增加趨近零的速度越快；當工作質體工作于亞共振態時，力傳遞系數在隔振頻率0與臨界隔振頻率比之間存在一個最大值，此最大值隨工作頻率向共振態接近而增大。當隔振頻率在0與臨界隔振頻率比之間變化時，特征幅值與力傳遞系數變化規律基本相同；但當隔振頻率比大于臨界隔振頻率比時，特征幅值隨隔振頻率比增加逐漸趨近于恒定值，且對應最大特征幅值的工作質體頻率比略大于1，隨工作質體頻率比遠離此值，特征幅值迅速下降。隨σ2r減小，特征幅值隨工作質體頻率比變化的差異越大，而隨σ2r的增大這種差異會逐漸消失。

（3）在振動系統工作于帶載狀態情況下，當隔振頻率比小于臨界隔振頻率比時，力傳遞系數較大。在隔振頻率比相同且大于臨界隔振頻率比時，對應于工作質體在亞共區確定的頻率比，隨σ2r減小，初始特征幅值增大，特征幅值放大倍數略有減小，最大力傳遞系數略有增大，最大參振物料系數減小。綜合各性能指標可以看出，較小的σ2r值，有利于提高振動系統綜合性能指標。

（4）振動激勵角越小，系統同步能力系數越大。當激振器安裝剛體作為物料箱時，工作質體與激振器安裝剛體的質量比對系統達到共振態時的最小同步能力系數影響不大；但當支撐剛體作為物料箱時，可以大大提高振動激勵角，增加系統有效激振力及系統的同步能力系數。系統結構可以保證兩偏心同步運行的穩定性。

［1］Blekhman I I．Synchronization in Science and Technology［M］．New York：ASME Press，1988．

［2］Blekhman I I．Method of direct separation ofmotions in the action of vibration on nonlinear dynamic system［J］．Izv，A N SSSR，MTT，1976，6：13－27．

［3］Wen BC，Fan J，Zhao CY，etal．Vibration synchronization and controlled synchronization in engineering［M］．Beijing：Science Press，2009．

［4］聞邦椿，李以農，張義民．振動利用工程［M］．北京：科學出版社，2005．

［5］Wen Bang-chun，Zhang Hui，Liu Shu-ying，et al．Theory and techniques of vibrating machinery and their applications［M］．Beijing，Science Press，2010．

［6］劉勁濤，劉杰，李小號，等．反共振時質體振幅最小的反共振振動機動力學分析與仿真［J］．振動與沖擊，2009， 28（9）：109－112．

LIU Jin-tao，LIU Jie，LI Xiao-hao，et al．Analysis and simulation of dynamics for a anti-resonant vibrating machine of the minimum amplitude［J］．Journal of Vibration and Shock，2009，28（9）：109－112．

［7］Zhao Chun-yu，Zhu Hong-tao，Bai Tian-yu，et al．Synchronization of two non-identical coupled exciters in a non-resonant vibrating system of linear motion［J］．Part I：Theoretical analysis，Shock and Vibration，2009，16（5）：505－516．

［8］Zhao Chun-yu，Zhu Hong-tao，Bai Tian-yu，etal．Synchronization of two non-identical coupled exciters in a non-resonant vibrating system of linearmotion［J］．Part II：Numeric analysis，Shock and Vibration，2009，16（5）：517－528．

［9］Zhao Chun-yu，Zhang Yi-min，Wen Bang-chun．Synchronization and general dynamic symmetry of a vibrating system with two exciters rotating in opposite directions［J］．Chinese Physics B，2010，19（3）：030301．

［10］趙春雨，劉戡，葉小芬，等．反向回轉雙機驅動振動系統的自同步理論［J］．機械工程學報，2009，35（9）：24－30．

ZHAO Chun-yu，LIU Kan，YIE Xiao-fen，et al．Theory of self-synchronization for a vibrating system with two exciters rotating in opposite directions［J］．Journal of Mechanical Engineering，2009，35（9）：24－30．

［11］陸啟韶．常微分方程的定性方法與分叉［M］．北京：北京航空航天大學出版社，1989．

［12］Zhao Chun-yu，Zhu Hong-toa，Zhang Yi-min，et al．Synchronization of two coupled exciters in a vibrating system of spatial motion［J］．Acta Mech Sin，2010，26（2）：477－493．

［13］趙春雨，王得剛，李杰，等．同向回轉雙機驅動振動系統的頻率俘獲［J］．應用力學學報，2009，26（2）：283－287．

ZHAO Chun-yu，WANG De-gang，LI Jie，et al．Frequency capture of a vibrating system with dual-motor drives rotating in the same direction［J］．Chinese Journal of Applied Mechanics，2009，26（2）：283－287．

Effects of dynam ic parameters on the performance of a three-mass vibrating machine

ZHAO Chun-yu，ZHAO Qian-bin，HE Bin，WEN Bang-chun
（School of Mechanical Engineering and Automation，Northeastern University，Shenyang 110819，China）

The dimensionless characteristic amplitude ofworkingmass（DCAWM），themagnification coefficient of characteristic amplitude（MCCM），the maximum coefficient of vibration of material（MCVM），the force transfer coefficient between vibration isolation frame and foundation（FTCBVIFF），the synchronization ability coefficient（SAC），and the critical frequency ratio of vibration isolationmass（CFRVIM）were proposed to describe the performance of a threemass vibratingmachine．The effects of dynamic parameters of system on the performance of the vibrating machine was investigated by numeric method．When the working mass operates in a state of supper resonance，the DCAWMand the FTCBVIFF decrease with the increase of frequency ratio of vibration isolation mass（FRVIM）．When the FRVIMis greater than the CFRVIM，with the increase of the FRVIM，the initial DCAWMand themaximum FTCBVIFF increase，and the MCCMand the MCVMdecrease．Hence，the smaller the FRVIMis，the better the performance of the vibrating machine is．The smaller the exciting angle is，the bigger the synchronization ability coefficient of the two exciters is．When the supporting rigid body serves asmaterial box，the synchronization ability coefficient increaseswith the increase of the ratio of the workingmass to themass of exciter installation body．The structural parameters of the system can satisfy the synchronization stability criterion．Anumerical simulation verifies the theoretical investigation results．

vibrating system；vibration isolation；self-synchronization；stability

TH113

A

10．13465／j．cnki．jvs．2015．12．013

國家自然科學基金資助項目（51075063）

2014－03－19 修改稿收到日期：2014－05－30

趙春雨 男，教授，博士生導師，1963年生