依托旋轉研究極限，函數思想破解難關

☉江蘇省南京市六合區實驗高級中學 王安寓

依托旋轉研究極限，函數思想破解難關

☉江蘇省南京市六合區實驗高級中學 王安寓

“直線與圓”是解析幾何的重要組成部分，其地位同圓錐曲線.很多考試都會命制質量上乘的考查直線與圓的位置關系的題目.求解直線與圓的位置的關系的題目，最關鍵的是靈活轉化——將題目所給的條件靈活轉化為相關的式子，要能透過表象看透本質，看透命題人的目的，看透命題人想考查的知識點，看透命題人想考查的數學方法，應用之求解.

題目1 （2014年江蘇南通五校聯考，18）已知△ABC的三個頂點A（-1，0）、B（1，0）、C（3，2），其外接圓為圓H.

（1）求圓H的方程；

（2）若直線l過點C，且被圓H截得的弦長為2，求直線l的方程；

（3）對于線段HB上的任意一點P，若在以C為圓心的圓上都存在不同的兩點M、N，使得點M是線段PN的中點，求圓C的半徑r的取值范圍.

易求得：（1）x2+（y-3）2=10；（2）x=3或4x-3y-6=0.

本文主要研究第三問.

分析1：由（1）知H（0，3）.解析幾何的一個特點是數形結合.首先作出適合題意的圖形，如圖1，觀察圖1，我們發現：此題中圓心雖定，但半徑不定——圓C在動；點P動帶動M、N動，而且M、N的位置對于一個點P還可能有第二種可能.四個動的元素間還沒有一個定其余隨之定的關系，而是既相互干擾又有變動.初讀題，覺得無從入手，找不到切入口.重新讀題，想到MN是圓的弦，而圓中既變（位置）又不變（長度）的弦是直徑，是不是從圓的直徑入手？點P是線段HB上的動點，是不是優先考慮HB的端點？連接HC、BC，易知|HC|＞|BC|，取CH的靠近C的三等分點M0，以C為圓心，以|CM0|=為半徑作圓，延長HC，與圓C交于N0，則|HM0|=|M0N0|，適合題意（如圖2）.當P是線段HB上任意一點時（不與H重合），連接PC并延長，與圓C交于M1、N1兩點，則|PM1|＜|HM0|=|M0N0|= |M1N1|，可將PM1N1繞P旋轉，則PM1變長，M1N1變短，到某一位置PMN，必有|PM|=|MN|，即該圓C適合條件.隨著圓C的半徑增大總可以用旋轉的方法找到適合題意的割線PMN；而當圓C的半徑太大時，直線HB與圓C不相離，不存在割線，不合題意；當圓C的半徑太小時，連接HC，與圓C交于M2、N2兩點，則|HM2|＞|M2N2|，而M2N2是圓C的最長的弦，無論怎樣旋轉都不會有|HM2|=|M2N2|，不合題意.從而求得圓C的半徑的范圍是

圖1

圖2

解析1：見分析1.

分析2：?P∈HB，都有P在圓C外，得|CP|-r＞0.|PM|= |MN|如何轉化？注意到MN是圓C的弦，因此聯系圓C的直徑，必有|MN|≤2r，PM是線段HB上任意一點與圓C上一點連線的長度，自然與圓心C有關，依據三角形中兩邊之差小于第三邊得|CP|-r≤|PM|，從而形成不等式鏈0＜|CP|-r≤|PM|=|MN|≤2r，再考慮?P∈HB，自然轉化為最值求解.

解析2：依題意得0＜|CP|-r≤|PM|=|MN|≤2r，即r＜|CP|≤3r恒成立.

分析3：從代數的角度思考，求出BH的方程，設出P、N的坐標，應用中點公式求得M的坐標，進而考慮M、N在圓C上，轉化為兩個圓有公共點問題，再轉化為函數的最值問題求解.

解析3：易求得直線BH的方程為3x+y-3=0，設P（m，n）（0≤m≤1），N（x，y）.

因為該方程組有解，所以兩個圓（以（3，2）為圓心、以r為半徑的圓和以（6-m，4-n）為圓心、以2r為半徑的圓）有公共點，所以2r-r≤≤2r+r.

易求得f（m）=10m2-12m+10，m∈［0，1］的值域為

點評：解析1是依托運動（旋轉）找到解決的方法.解析2是由點P在圓C外得|PC|-r＞0，由三角形兩邊之差小于第三邊和圓的弦中直徑最長，得到PC-r≤PM，MN≤2r，再由條件M為NP的中點溝通，形成一個不等式鏈，通過恒成立達到解題的目的，這種求解的想法是源于前面的分析，是通過特殊到一般才形成的解題過程.?P∈HB，都有r＜|CP|≤3r成立，自然運用函數思想，轉化為最值問題求解.求解的過程簡單，而思維的過程艱難.解析1呈現復雜而學生易于理解；解析2呈現簡單而學生不易想到.如果把解析1的求解過程縮減，用相關的數學式子表征，那么就得到解析2.解析1是解析2的動態演示.解析3是從代數的角度入手，將點點、點圓的位置關系通過式子表示出來，進而轉化為函數的最值問題求解.解析3是解析2的代數化.

變式1：已知點B（1，0）、H（0，3）、C（3，2），P為線段HB上任意一點，過點P作以C為圓心的圓的割線PMN，與圓C交于M、N，設M為PN的中點，則由所有滿足上述條件的圓C組成的圖形的面積為______.

變式2：已知點B（1，0）、H（0，3）、C（t，2），P為線段HB上任意一點，過點P作以C為圓心、以為半徑的圓的割線PMN，與圓C交于M、N，設M為PN的中點，則實數t的取值范圍是_________.

變式3：已知點B（1，0）、H（0，3）、C（2，s），P為線段HB上任意一點，過點P作以C為圓心、以為半徑的圓的割線PMN，與圓C交于M、N，設M為PN的中點，則實數s的取值范圍是_________.

變式4：已知點B（1，0）、H（0，3）、C（t，s），P為線段HB上任意一點，過點P作以C為圓心、以為半徑的圓的割線PMN，與圓C交于M、N，設M為PN的中點，則所有適合條件的圓心C的軌跡所構成的圖形的面積是________.

變式5：已知點B（1，0）、H（0，3）、C（t，s），P為線段HB上任意一點，過點P作以C為圓心、以為半徑的圓的割線PMN，與圓C交于M、N，設M為PN的中點，則所有適合條件的圓的軌跡所構成的圖形的面積是________.

變式6：已知點B（1，0）、H（0，3）、C（3，2），P為線段HB上任意一點，過點P作以C為圓心的圓的割線PMN，與圓C交于M、N，設（λ＞0，λ為已知的數），則圓C的半徑的取值范圍是_________.

高考鏈接

題目2 （2014年江蘇，18）如圖3所示，為保護河上古橋OA，規劃建一座新橋BC，同時設立一個圓形保護區.規劃要求：新橋BC與河岸AB垂直；保護區的邊界為圓心M在線段OA上并與BC相切的圓，且古橋兩端O和A到該圓上任意一點的距離均不少于80m.經測量，點A位于點O正北方向60m處，點C位于點O正東方向170m處（OC為河岸），tan∠BCO=

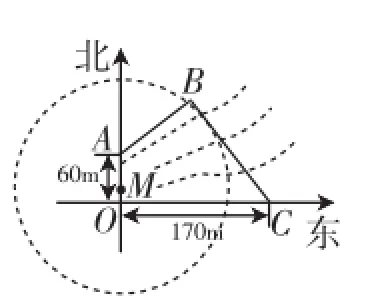
圖3

（1）求新橋BC的長.

（2）當OM多長時，圓形保護區的面積最大？

題 目 3 （2011年 江 蘇 ，14） 設 集 合 A=≤（x-2）2+y2≤m2，x、y∈B =（｛x，y）|2m≤x+ y≤2m+1，x、y∈R｝，若A∩B≠?，則實數m的取值范圍是_______.

題目4 （2012年江蘇，12）在平面直角坐標系xOy中，圓C的方程為x2+y2-8x+15=0，若直線y=kx-2上至少存在一點，使得以該點為圓心、1為半徑的圓與圓C有公共點，則k的最大值是_________.

題目5 （2013年江蘇，17）在平面直角坐標系xOy中，點A（0，3），直線l：y=2x-4.設圓的半徑為1，圓心在l上.

（1）若圓心C也在直線y=x-1上，過點A作圓C的切線，求切線的方程；

（2）若圓C上存在點M，使|MA|=2|MO|，求圓心C的橫坐標a的取值范圍.

直線與圓的呈現千姿百態、百媚千嬌，其求解過程美不勝收、令人流連，其答案馭繁于簡、合理平實.如果再深層探究，那么會更搖曳生姿，會變換得美輪美奐，會讓你進入另一個仙景——圓錐曲線景觀.

1.王安寓.圓背景 橢圓題 推陳出新淡出奇［J］.中學數學（上），2013（9）.A