一道調(diào)研試題的多視角求解

☉江蘇省南京市秦淮中學 周國溢

一道調(diào)研試題的多視角求解

☉江蘇省南京市秦淮中學 周國溢

一、試題呈現(xiàn)

題目（南京、鹽城2014屆高三年級第二次模擬考試第17題）如圖1，經(jīng)過村莊A有兩條夾角為60°的公路AB、AC，根據(jù)規(guī)劃擬在兩條公路之間的區(qū)域內(nèi)建一工廠P，分別在兩條公路邊上建兩個倉庫M、 N（異于村莊A），要求PM=PN=MN=2（單位：千米）.如何設計，使得工廠產(chǎn)生的噪聲對居民的影響最小（即工廠與村莊的距離最遠）.

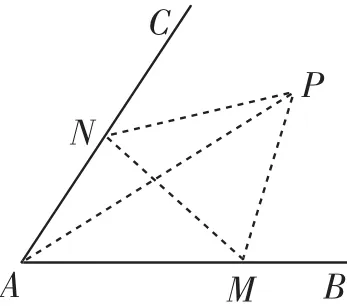
圖1

二、視角選擇

分析：根據(jù)題意易知，倉庫與工廠三點構成的三角形始終為等邊三角形，并且要求工廠對村莊的影響最小，即PA的距離最長.綜合上述解讀，可以將題意理解成：將一邊長為2的等邊三角形放置在一個60°角的區(qū)域內(nèi)，使三角形的兩頂點分別置于角的兩邊上，并且第三個頂點到A點的距離最大.明顯，這是一道求最值的問題，按一般的解題思路，求最值問題往往會利用函數(shù)的有界性、不等式的有界性，或者利用圖形本身的幾何特性限制范圍.

（一）視角一——函數(shù)的有界性

要利用函數(shù)的有界性，首先，構造相關函數(shù)，找出函數(shù)定義域，對于本題易知所要構造的目標函數(shù)是三角函數(shù)，然后，求出目標三角函數(shù)的上界，即可求出最大值.

1.單刀直入，解三角形

本解單刀直入，從正余弦定理切入，將等邊三角形的邊MN與角的一邊AM所形成的角作為自變量θ，利用解三角形的相關知識將所求線段長度轉化成關于θ的三角函數(shù)，利用三角函數(shù)的有界性，求其上界得到最大值.

2.直角特殊，構造直角

過點P作AB的垂線PD，易知PA2=PD2+AD2，要求PA，需將勾股定理表達式轉化成三角函數(shù)的表達式即可.

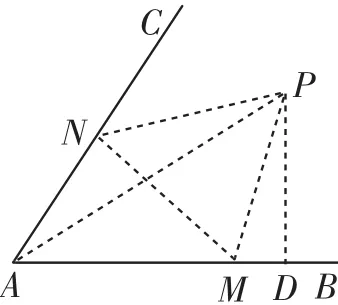
圖2

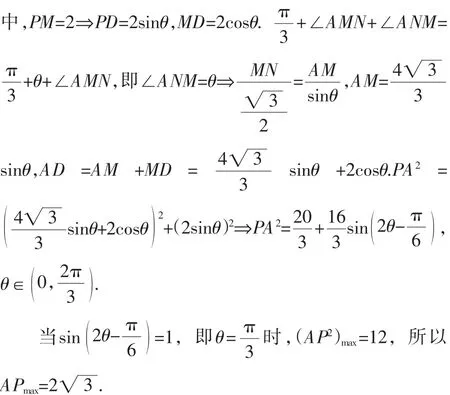
本解法在解題思路上與上解出于同源，但卻不同路.其不同之處即所利用的三角形為直角三角形，而構