如何利用“數形結合”高效解題

☉湖北省孝感高級中學 徐運麗

如何利用“數形結合”高效解題

☉湖北省孝感高級中學 徐運麗

數形結合的思想，實質上是將抽象的數學語言與直觀的圖形結合起來，也就是對問題中的條件和結論分析其代數含義，挖掘其幾何背景，在代數與幾何的結合上尋找解題思路.要注意培養學生這種數形結合的意識，逐步使學生胸中有圖，見數思圖，逐步開拓他們的思維視野.縱觀多年來的高考試題，巧妙運用數形結合的思想方法解決一些抽象的數學問題，可起到事半功倍的效果，數形結合的重點是研究“以形助數”.用好“以形助數”，同時兼顧“以數助形”，可以給解題帶來簡捷、高效.

一、以形助數——數缺形時少直覺

“以形助數”，即根據數的結構特征，構造出與之相適應的幾何圖形，并利用圖形的特征和規律，解決數的問題.例如利用“形”的直觀來研究方程根的情況，討論函數的值域（或最值），求解變量的取值范圍等.“以形助數”不僅直觀易于尋找解題途徑，而且能避免繁雜的計算和推理，簡化解題過程.

例1 已知函數f（x）滿足f（x+1）=f（x-1），且f（x）是偶函數，當x∈［0，1］時，f（x）=x2，若在區間［-1，3］內，函數g（x）= f（x）-kx-k有三個零點，則實數k的取值范圍是（ ）.

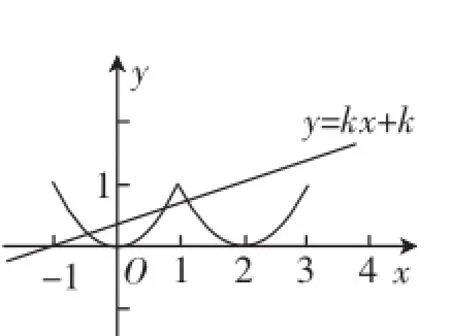
圖1

解析：因為函數f（x）滿足f（x+1）=f（x-1），所以函數f（x）是周期為2的周期函數.又f（x）是偶函數，且當x∈［0，1］時，f（x）=x2，故可畫出函數f（x）在區間［-1，3］的圖像.由于函數g（x）=f（x）-kx-k有三個零點，所以函數f（x）在區間［-1，3］上的圖像與直線y= kx+k有三個交點，如圖1所示.把點（3，1）代入y=kx+k，可得k=，將（1，1）代入y=kx+k，可得k=，數形結合可得實數k的取值范圍是故選C.

點評：討論方程的解（或函數的零點）可構造兩個函數，使問題轉化為討論兩曲線的交點問題，但用此法討論方程的解一定要注意圖像的準確性、全面性，否則會得到錯解.

例2 （2012年浙江理科第17題）設x＞0時，均有［（a-1）x-1］（x2-ax-1）≥0，則a=_________.

分析：作為客觀題的最后一題，有一定的難度，主要考查的是靈活處理問題的能力及數形結合的思想.根據當年的考試和評卷情況，此題的得分率是不高的，其原因是缺少數形結合思想，許多考生陷入了常見的兩種思路模式.

（1）由題意分兩種情況：或

（2）令f（x）=［（a-1）x-1］（x2-ax-1）=（a-1）x3-（a2-a+ 1）x2+x-1，等價于f（x）≥0在（0，+∞）上恒成立，再利用導數討論求解.

這兩種方法過程繁雜，甚至無法進行下去，半途而廢.而用數形結合思想解決此題則比較清楚明了.

解：（數形結合法）將原題化為：［ax-（x+1）］［ax-（x2-1）］≤0，分別作出f（x）=ax，g（x）=x+1，h（x）=x2-1的圖像，如圖2所示.要x＞0時，滿足［f（x）-g（x）］［f（x）-h（x）］≤0，等價于x＞0時，f（x）的圖像在g（x）與h（x）之間.所以f（x）=ax只能過g（x）與h（x）的交點，此時a=

圖2

也可以直接從y1=（a-1）x-1，y2=x2-ax-1的圖像都過點P（0，-1）分析，如圖3所示.y1的圖像與x軸的交點M必須在x軸的正半軸上，否則不能保證x＞0時，y1y2≥0，所以a＞1.這時y2的圖像必須過點M才能使x＞0時，恒有y1y2≥0.

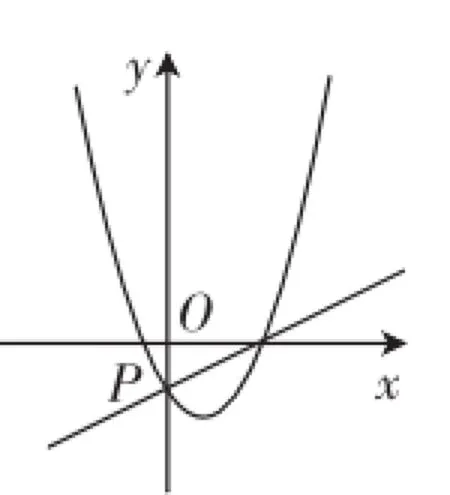
圖3

點評：求參數范圍或解不等式問題經常聯系函數的圖像，根據不等式中量的特點，選擇適當的兩個（或多個）函數，利用兩個函數圖像的上、下位置關系轉化為數量關系來解決問題，往往可以避免煩瑣的運算，獲得簡捷的解答.

二、以數定形——形缺數時難入微

借助圖形可以方便地處理一些數學問題，從而提高探究問題的能力，但過分地依賴直觀圖形，缺乏理性的認知深度，極有可能造成“眼見為虛”的被動局面.“以數定形”，即將圖形信息部分或全部轉換成代數信息，削弱或清除形的推理部分，使要解決的形的問題轉化為數量關系的討論.常用的有借助于幾何軌跡所遵循的數量關系、運算結果與幾何定理的結合.

例3 如果曲線y2=6x與（x-m）2+y2=4沒有公共點，求實數m的取值范圍.

圖4

錯解：如圖4，考慮半徑為2，圓心為（m，0）的圓與拋物線y2=6x的兩個相切的臨界位置.一種是外切于原點，此時m=-2.另一種是相切于兩點，則聯立方程組消去y得x2-（2m-6）x+ m2-4=0（*），令Δ=0，解得m=.綜合以上兩種臨界位置，結合圖形，可知m的取值范圍是（-∞，-2）∪

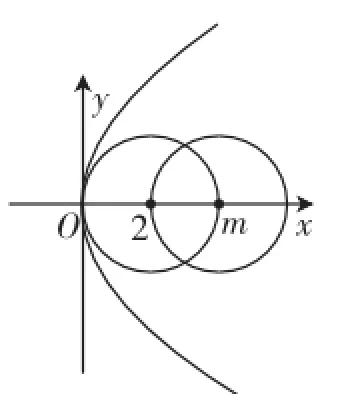
圖5

正解：兩曲線有公共點的充要條件是方程（*）至少有一個非負實數根，即或解得-2≤m≤2，故兩曲線無公共點時m的取值范圍是（-∞，-2）∪（2，+∞）.

三、數形兼顧——數形結合百般好

數缺形時少直觀，形缺數時難入微，只有“數”與“形”相輔相成，才能達到靈活運用數形結合思想.圖形能提供直觀的視覺信息，從而降低思維的起點，突破思維障礙.代數方法具有表述容易、結構嚴謹、結論精確等優點.若能靈活地將兩者融為一體，數學解題將變得游刃有余！

解析：因為方程f（x）=kx2有4個根，即方程=kx2有 4個根，顯然x=0為方程的一個根，則只要方程=kx2再有3個不同的非零根即可.而當x≠0時，=構造函數g（x）=，則只要函數g（x）的圖像與函數y=的圖像再有3個交點即可，在同一坐標系內畫出兩個函數圖像，由圖像容易看出當0＜＜1，即k＞1時，兩函數的圖像有3個非零交點，即對應的方程有3個不同的非零根.綜上可知：當k∈（1，+∞）時關于x的方程f（x）=kx2有4個不同的實數解.

點評：題目本身是有關方程解的問題，經過上述的處理，將方程解的問題轉化成兩函數圖像的交點問題，利用數形結合，直觀簡捷，比用純代數方法求解要方便快捷許多.

數形結合，不僅是一種有效的解題方法，更是一種重要的數學思想和思維方式，它兼具了數的嚴謹性與形的直觀性兩個方面的長處，是優化解題過程的重要途徑，也是對知識和能力的集中反映.誠如華羅庚大師所言：“數形相倚依，‘數’準確而抽象，‘形’形象而粗略，二者的結合溝通了數與形的聯系，從而使得用數量的抽象特性來說明圖形形象直觀的事實，同時又用圖形直觀具體的特征來說明數量的抽象性質，這正是數形結合的本質所在.”F