淺析“向量坐標系”在解題中的應用

☉江蘇省蘇州市田家炳實驗高級中學 王 耀

淺析“向量坐標系”在解題中的應用

☉江蘇省蘇州市田家炳實驗高級中學 王 耀

文1中，筆者通過建立“向量坐標系”解決了一類高考題.事實上，對“”這種形式的許多問題，［2］還可利用平面向量基本定理去進一步研究“向量坐標系”，并通過與平面直角坐標系的類比，得到向量坐標系中的一些重要推論，從而可直接基于向量視角順利解決問題.

一、“向量坐標系”的三要素

1.認識“向量坐標系”中的“點”的屬性

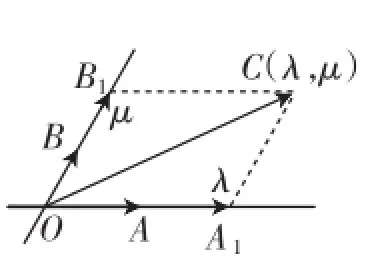
圖1

2.分析“向量坐標系”中的距離、夾角和數量積

這里，以剛結束的一道2014年卓越聯考自主招生試題為例來研究“向量坐標系”中的兩點距離問題.

試題 n1、n2是兩個夾角為θ的單位向量，以n1、n2為基的坐標系中，A（x1，y1），B（x2，y2），求|AB|.

首先，以n1方向為x軸建立平面直角坐標系，此時n1=（1，0），n2=（cosθ，sinθ），那么由A（x1，y1）知得到A（x1+y1cosθ，y1sinθ）；同理，可知B（x2+y2cosθ，y2sinθ），則可得到|AB|=

事實上，若建立向量坐標系的話，只要通過向量基本運算即可得到同樣的結果，這也說明選擇不同的坐標系，距離是不變的.具體解法如下：

設n1、n2的交點為O，則那么=（x2-x1）n1+（y2-y1）n2，那么（y2-y1）2+2（x2-x1）（y2-y1）n1n2，利用n1n2=cosθ即可解得

此時，即可探究向量坐標系中的兩個向量的數量積定義與計算公式，不妨設a=一方面：a·b=（x1n1+y1n2）·（x2n1+y2n2）=x1x2+y1y2+（x1y2+ x2y1）n1·n2=x1x2+y1y2+（x1y2+x2y1）cosθ； 又由定義a·b=，及余弦定理：=|a|·|b|·cos〈a，b〉，則可知在向量坐標系中，向量數量積a·b=|a|·|b|·cos〈a，b〉仍然成立，這與平面直角坐標系中的結論一致.并且，向量極化恒等式a·b=和平行四邊形公式|a+b|2+|a-b|2=2（|a|2+|b|2）依然成立.

3.探究“向量坐標系”中的“線”的本質

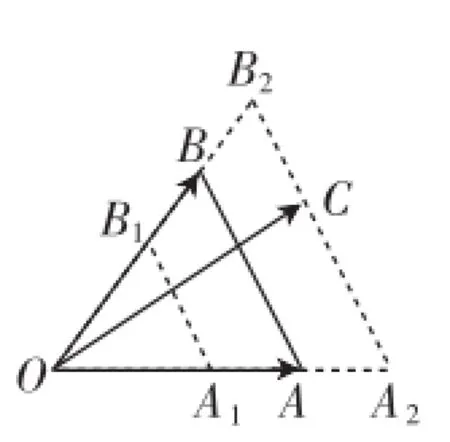
圖2

文1中，基于平面向量基本定理的推論進一步討論了一類可化為“”的向量值線性規劃區域問題，即將問題轉化為共起點的基底向量，從而研究k= λ+μ的取值范圍，其中k=，如圖2所示.那么，對于向量坐標系中任意的一條線aλ+bμ=c（a，b，c∈R）又表示何種意義呢？首先，分別考慮如下情形.

評注：事實上，此處也可用平面幾何知識，過點C分別作OA、OB的平行線，由平行線分線段成比例定理更容易得到，同理也能夠得到向量在直線μ=λ上.

二、例題賞析

例1 （1）（2013年北京（文）14）已知點A（1，-1），B（3，0），C（2，1）.若平面區域D由所有滿足（1≤λ≤2，0≤μ≤1）的點P組成，則區域D的面積為_________.

（2）（2014年福建預賽8）已知點A（1，-1），B（4，0），C（2，2）.平面區域D由所有滿足（1＜λ≤a， 1＜μ≤b）的點P（x，y）組成.若區域D的面積為8，則a+b的最小值為_________.

（3）已知-1≤x≤3，1≤y≤4，|a|=1，|b|=2，〈a，b〉=60°，則|xa+yb|的取值范圍為_________.

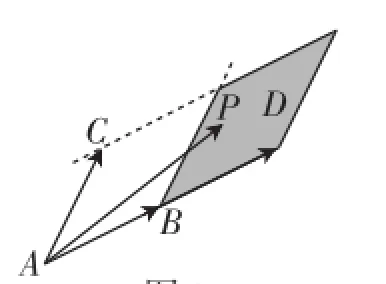
圖3

那么區域D的形狀為平行四邊形，夾在兩對平行線λ=1，λ=2與μ=0，μ=1之間，其面積與以為鄰邊的平行四邊形面積相等，即

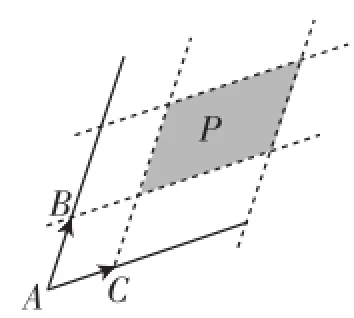
圖4

由題意可知SP=（a-1）8（a-1）（b-1）=8，即（a-1）（b-1）=1.

（3）建立向量坐標系（如圖5），分別作直線x=-1，x=3，y=1，y=4，易知|xa+yb|min=|m|，|xa+yb|max=|n|.

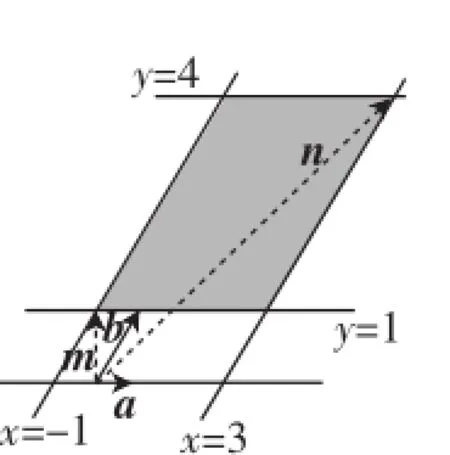
圖5

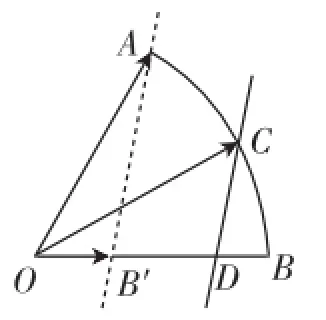
圖6

例2（1）（2013年浙江省杭州市高三一模17）如圖6，在扇形OAB中，∠AOB=60°，C為弧AB上的一個動點，若則x+3y的取值范圍是_________.

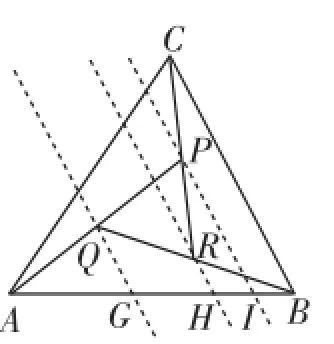
圖7

（3）（2014年浙江省寧波市高三模擬）已知點O是△ABC的外心（外接圓的圓心），且AB= 3，AC=4，若存在非零實數x，y，使得且x+ 2y=1，則cos∠BAC=_________.

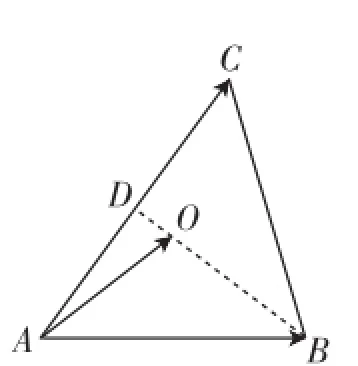
圖8

（4）（2014年蘇錫常鎮高三第一次調研12）如圖8，在△ABC中，BO為邊AC上的中線，，則λ的值為_________.

（2）如圖7所示，分別過點Q、R、P作BC的平行線，分別交AB于G、H、I三點，則可設AG=GI=x，IB=y，HI=z；BH= GH=y+z，那么AB=AG+GH+IB=x+x+y；AB=BH+HG+AG= 2（y+z）+x.由此可知x=y+2z.又由P為CR的中點，可知HI= IB，即y=z，那么x=3z.因此，由可知m+n==

評注：此題中若沒有“若存在非零實數x、y”這個條件，結果將會發生變化.通過上述解析過程發現，當x=0， y=時，△ABC的外心點O和點D重合，此時△ABC為直角三角形，且AB⊥BC，則cos∠BAC=，故結果將會有兩解.

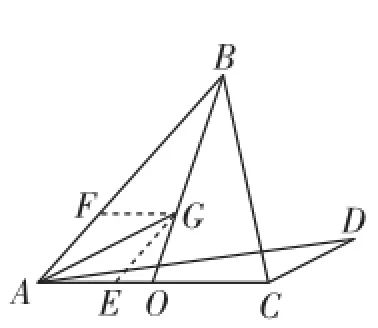
圖9

（4）在圖9中，過點G作AB的平行線交AO于點E，作AC的平行線交AO于點F，由可知即有=；同理那么

例3 （1）（2014屆成都二診數學（文科）試題15）已知單位向量i、j的夾角為θ（0＜ θ＜π，且θ≠），若平面向量a滿足a=xi+yj（x，y∈R），則有序實數對（x，y）稱為向量a在“仿射”坐標系Oxy（O為坐標原點）下的“仿射”坐標，記作a=（x，y）θ.有下列命題：

①已知a=（2，-1）θ，b=（1，2）θ，則a·b=0；

③已知a=（x1，y1）θ，b=（x2，y2）θ，則a-b=（x1-x2，y1-y2）θ；

④已知=（1，0）θ，=（0，1）θ，則線段AB的長度為2sin

其中為真命題的是________（寫出所有真命題的序號）.

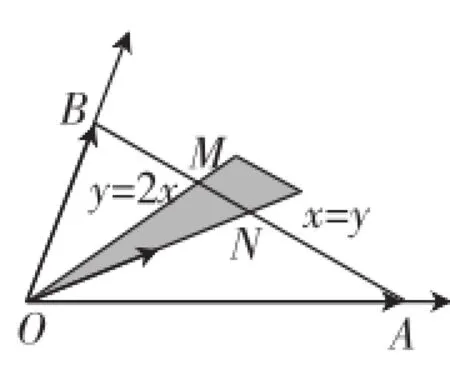
圖10

①x≥0，y≥0；②x-y≥0；③x-y≤0；④x-2y≥0；⑤2x-y≥0.

解析：（1）①由前文分析知a·b=（2i-j）·（i+2j）=3i·j= 3cosθ，當且僅當θ=90°時，a·b=0.故①錯.

②在向量坐標系下考慮，若向量a、b的夾角取到最小值0時，則向量a、b共線且同向，那么x=y＞0；反之，若x= y＜0時，向量a、b共線但是反向，故它們夾角取到最大值π.因此，②錯.

③a-b=（x1-x2）i+（y1-y2）j=（x1-x2，y1-y2）θ.

綜上可知，③④為真命題.

（2）建立如圖10所示的“向量坐標系”，仿照平面直角坐標系，首先同樣得到：x≥0，y≥0.

此外，線段MN上滿足x+y=1；右上方的平行線段上滿足x+y=k（k＞1）.故圖10中所示區域內的系數滿足：

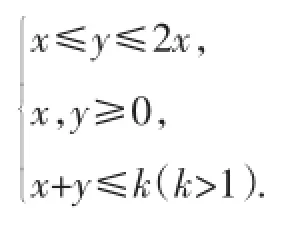
三、題后總結

文中，筆者從純向量的角度分析了“向量坐標系”的特性，并成功應用到一系列可化為此背景的高考或模考試題中.常規做法主要是建立直角坐標系進行向量坐標運算或者直接利用向量基本運算，這種傳統的處理方式在解決問題時，耗時耗力；而本文提供的這種“幾何通法”的優勢主要體現在：利用平面向量的基本定理，將一類涉及基底的線性表示系數之和的問題，化歸為建立基底“向量坐標系”進行問題分析.這種做法既能避免煩瑣的代數運算，又能夠充分體現向量的“形”的幾何優勢，將“形”的魅力展現到極致.

在教學中，要對重要知識點有選擇地“把書讀厚”，即指要讓學生明白知識的核心和本質是什么，它的上位知識是什么，以及構成知識的基本要素又有哪些，它的用處在哪兒.結合對文中相關內容的教學實踐來看，筆者并沒有涉及“仿射坐標系”等高深的概念，而是直接用“向量坐標系”來描述，并且通過與平面直角坐標系的類比而研究得到向量坐標系中的許多性質，這樣的處理方式適合學生的認知結構，避免讓學生覺得很難很高深，反而容易被學生理解和掌握.［3］

綜上所述，作為教師，要了解知識體系結構，深諳個中的關系，并自覺地指導和幫助學生認識問題，參悟本質，形成思維.只有這樣，作為求知者的學生，才能從被動的解題中解放出來，知曉知識的來龍去脈，深究核心知識的數學本質，從而做到了然于心，方能運用自如.

1.王耀.一類可化為向量值線性規劃問題的研究及其應用［J］.中學數學（上），2014（3）.

2.蔣明建.破解向量難題 挖掘潛在信息［J］.中學數學（上），2013（9）.

3.齊民友.中學數學教學中的向量［J］.數學通報，2007（4）.F