城市軌道交通運營管理專業也需要學概率

柯肇螢

【摘 要】概率論與數理統計是數學的一個重要分支，它是一門用確定數學作為工具研究不確定的隨機現象、挖掘外在表象下的內在客觀規律的科學。目前，城市軌道交通行業迅猛發展，要求人才素質不斷提高，軌道交通運營管理中隨機現象又無處不在，因此中等職業學校的學生學好概率，用好概率在今后的崗位上會受益匪淺。概率教學的核心問題恰是讓學生了解隨機現象與概率的深刻意義，而理解把握概率與數理統計的概念，對于整體把握概率學習是重中之重。本文就學習概率的必要性、概率的定義、在概率概念理解中常見的誤區及概率分布的應用四方面談談自己的看法。

【關鍵詞】概率；頻率；獨立性；分布

一、時代背景

人人學有價值的數學，人人都能獲得必需的數學，不同的人在數學上得到不同的發展。在信息社會，收集、整理、描述、展示和解釋數據，根據情報作出決定和預測，已成為公民日益重要的技能，是每個公民基本素養的一部分。當今的城市軌道交通運營管理專業已經進入數字化經營的時代。城市軌道交通運營專業的發展對綜合專業人才的需要也越來越迫切。大量的事實表明，城市軌道交通行業的競爭歸根結底都將涉及綜合專業人才的競爭，城市軌道交通運營管理專業中隨機現象如：運輸計劃與運輸能力、列車運行組織與調車工作、客流預測與分析、票務管理、等問題又無處不在，因此在中職學校對學生進行概率和統計知識的普及是非常必要的。例如，日常生活中，我們經常會聽到：“某地區今天降水概率是70%。”、“分時段的客流分析，運能與運量相匹配”、“斷面客流短時預測。”概率與數理統計所提出的“運用數據進行推斷”的思考方法，已經成為現代社會一種普遍適用并且強有力的思維方式。

概率教學的核心問題是讓學生了解隨機現象與概率的意義，培養隨機觀念。弄清隨機變量的取值規律是用概率和分布刻畫的，會用隨機觀點處理隨機現象，知道統計結果是概率地呈現的，可能有誤差。因此，作為職業學校數學教師，引導學生正確理解隨機事件發生的不確定性及其頻率的穩定性，并嘗試澄清日常生活中遇到的錯誤認識；讓學生初步學會把一些實際問題化為古典概型。讓我們的學生學好概率，用好概率知識，培養高素質、創新型、綜合管理能力人才，以便日后更好地服務社會，如何更好地把握教材，服務專業，已成為當務之急。

二、概率的概念

在當今信息爆炸的年代，任何人不要說掌握全部科學知識，即使是全面掌握某一學科的知識都是不可能的。但各學科都有其特有的學科思想。知識體系就是在這種學科思想的指導下建立起來的。理解把握概率與數理統計的概念，對于整體把握概率教學是重中之重。

傳統的處理方法：隨機抽樣→總體→描出黑體字讓學生去背。

概率、總體、樣本的概念很復雜，對高中學生難以嚴格地說清楚，中專里只要描述即可。

著名數學家柯朗在《數學是什么》一書中的一段話：“世世代代以來，數學家一直把他們研究的對象，例如數、點等等，看成實實在在的自在之物。但是，至于點、線、數，“實際上”是什么，這不可能也不需要在數學科學中加以討論。“可驗證”的事實只是結構和關系：兩點決定一直線，一些數按照某些規則組成其它一些數，等等。基本的數學概念必須抽象化，這一見解是近代公理化發展中最重要和最豐富的成果之一”。其實概率的概念可以和點、線、面一樣看作是描述性概念。

概率的統計定義通常可以這樣敘述：在相同的條件下做大量的重復試驗，一個事件出現的次數m和總的試驗次數n之比，稱為這個事件在這n次試驗中出現的頻率。當試驗次數n很大時，頻率將“穩定”在一個常數附近，n越大，頻率偏離這個常數大的可能性越小.這個常數稱為該事件的概率.這里的定義就是描述性的。定義中的“可能性”，指的就是概率。

三、概率概念的理解

概率的概念應該從整體上把握理解，定義理解中的幾點誤區：

誤區1：所有不確定現象都是概率論研究的對象

事實上，并不是所有不確定現象都是概率論研究的對象。我們所討論的現象是可以做“重復試驗”的，例如：某球星是否退役，她今天是否不高興，等等。這類問題沒有重復試驗的意義，屬于人們的主觀猜測與愿望，并非概率論研究的對象。概率論描述的是可以重復試驗的模型。如買彩票中獎率的問題及乘客流動性等問題。

誤區2：結果的隨機性等于結果未知

事實上，結果的隨機性不同于結果未知。 例如，拋擲一枚硬幣，結果雖然隨機，但投擲結果不是正面幣值朝上，就是反面“國徽”朝上。再如，列車一旦運行，乘客的數量，雖然隨機，不能事先預知，但結果是三種，一種是達到基本客流量，一種是沒有達到基本客流量，一種是超過基本客流量。

多次拋擲一枚質地均勻的硬幣，隨著拋擲次數的不斷增加，正面朝上的頻率就在0.5附近擺動，拋擲次數越多，擺動范圍越小，而一枚質地均勻的硬幣正面朝上的概率一直都是0.5。

誤區4：概率=分布

事實上，概率反映的是“多次試驗”中頻率的穩定性，例如：擲骰子是四點出現的 “概率等于六分之一”決不等于“擲六次骰子中，四點出現一次”；即使告訴你中獎的概率為1/1000，但你買1000張獎券卻不一定能中獎。

誤區5：小概率事件就一定不發生。

事實上，小概率事件，發生概率雖小，但也會出現。不然就不會有馬航失聯；列車的安全門擠壓致人死亡的事故了。相反，大概率事件也不一定一定發生。例如：天氣預報今天降水概率是80%，但可能晴空萬里；明天的降水概率為10%，卻瞬間電閃雷鳴，概率并不提供確實無誤的結論。

誤區6：概率大就好

例如：甲校升學率為99%，乙校升學率為80%。人們自然愿意入甲校，盡管你可能入甲校沒有考上大學，入乙校卻考上大學。但人們還是認為甲校比乙校好，拼命進甲校，這是很盲目的，其實升學還有很多條件的，要科學分析，概率大不是絕對好，但從整體方面來說還是好的。又如兩個地鐵運營公司招聘，甲公司錄取率為50%，乙公司錄取率為70%，那么乙公司就一定比甲公司容易加入嗎？當然不一定。也許甲公司是對員工的個人素質需求較高，一般應聘者滿足不了。

誤區7：事件出現概率具有關聯性

例如，在買彩票時，有人說過去中獎的號碼里某一數碼，比如“15”出現最多，下次一定還會出現。“7”，在過去出現最少，由于每個數出現的機會是一樣的，因此，下次“7”出現的機會就大了，應該買“7”這個號碼，這些說法是不科學的。如果能認識到每次抽獎都是獨立的，那么不難看出上述的說法都是錯誤的，要學會用事件的獨立性概念來分析周圍的一些現象。

又如早晚高峰出行的問題，每天早7：00～8：30、晚5：00～6：30乘客較多形成早晚高峰，中午10：30～15：00乘客少形成客流空閑，當一個人要出行時，若選在早晚高峰出行，此時交通運營管理的作用是非常關鍵的，如何利用概率數理統計知識，選好出行時間，即目的地準時到達，又不受交通擁擠影響，是需要好好思考研究的。其實乘客完全可以利用時間差，錯過早晚高峰出行，既節約時間，又愉悅出行。

四、概率分布的應用

任何一種研究總是把未知的，不認識的事物逐漸變為已知的，可以認識的事物。 “了解”一個隨機現象是指：知道①這隨機現象中所有可能出現的結果。②每個結果出現的概率。最重要的隨機分布有如二項分布、正態分布等等，它們描述了隨機現象中最有用最常見的情形。隨機現象的分布列非常有用。

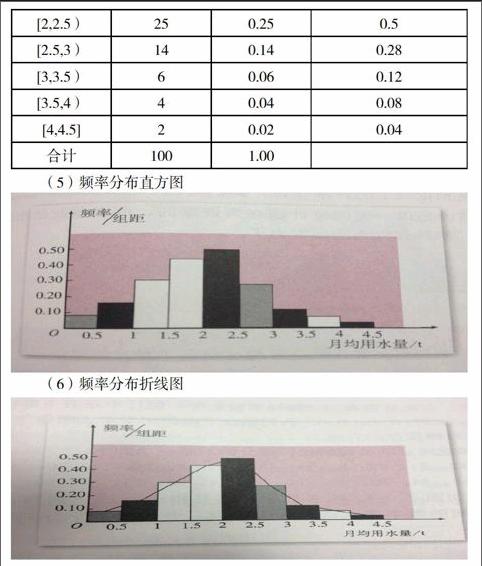
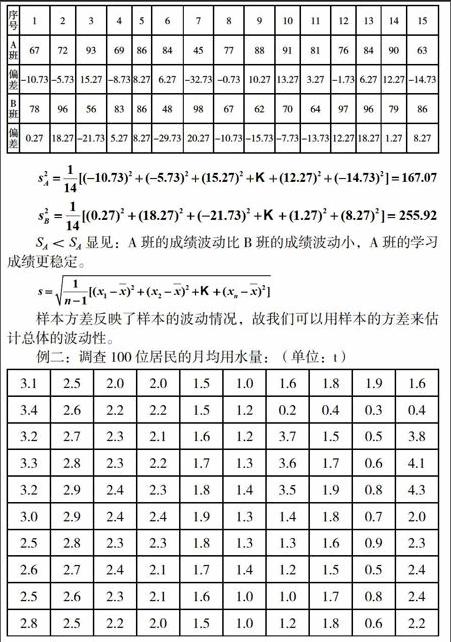
顯見，根據樣本數據的頻率分布，推測這個城市全體居民月均用水量分布的大致情況，也就是根據樣本的頻率分布，大致估計總體的分布。因為這種估計是以一定的統計調查為依據的，所以據此給市政府提出每位居民月用水量標準的建議，就具有較強的說服力了。用此方法同樣可以提供客流峰值數據，為城市軌道交通運營管理服務。

五、結語

“用數字說話”這是我們經常可以聽到的一句話，但是，即使學了一些概率統計知識，也不會一下就解決問題。例如：在前面講到的早晚高峰問題中，當一個人要出行時，盡管他知道了高峰出行的難度，還會在可以避免的前提下愿意選擇高峰出行。又比如他學過概率課后，知道抽簽與順序無關，但在實際生活中，碰到抽簽的事，他還是拼命地搶，爭取先抽到。因此，作為中職數學教師既要吃透教材培養學生的隨機意識，又要科學地講有價值的數學。一定要先把握好其概念、內涵，才能便于知識的普及。

參考文獻：

[1]《都市快軌交通》.北京交通大學主辦，2015.1.

[2] 王孝玲著.《教育統計學》.華東師范大學出版社.

[3] 張飴慈著.《談談中學概率的教學》.首都師范大學數學系.

[4] 周楷翠著.《七年級<統計與概率>教學分析》.資陽市簡陽城北中學.

[5]《數學3（必修）A版》.課程教材研究所.中學數學課程教材研發開發中心編著.人民教育出版社.