基于運輸問題的求解方法探討
段連偉 牛鳳秋 劉芬


[摘要]運輸問題是運籌學的一個分支,是線性規劃的特殊形式。它研究的是如何在一個大物資調運中,制定出一個由若干個產地將物資根據已知的運輸交通網運到各個銷售地的方案,使得總運費最小。利用Matlab依據遺傳算法的理論來計算出最佳結果是很有必要的,文章以運輸問題為例闡述了基于Matlab 的定量分析方法,解決了運輸最優方案求解這一大難題,可以廣泛應用于物流配送領域。
[關鍵詞]Matlab;遺傳算法;產銷平衡;產銷不平衡;表上作業法
[DOI]1013939/jcnkizgsc201533073
1問題陳述和正文內容
運輸是物流功能中最基本的功能。為了降低物流成本,我們有必要研究物流運輸中如何組織物資調運才能使總運輸成本最低這一重要問題。利用Matlab優化工具箱,可以求解線性、非線性、多目標和二次規劃等大中型問題,為優化方法在工程中的實際應用提供了更快捷的途徑。
在Matlab中構建函數l(x)解決線性規劃問題。運輸問題的最優解本質屬于極值問題,極大值問題的求解可以轉化為極小值問題,因此在Matlab中以求極小值為標準形式,構建的函數l(x)的具體格式如下:
[X,v,e,o,l]=l(F,A,b,m,n,M,N,P,Z)。
式中:X為問題的解向量;F為由目標函數的系數構成的向量;A為一個矩陣;b為一個向量,表示線性規劃中不等式約束條件,A,b是系數矩陣和右端向量;m和n為線性規劃中等式約束條件中的系數矩陣和右端向量;M和N為約束變量的下界和上界向量;P為給定的變量的初始值;Z為控制規劃過程的參數系列;v為優化結束后得到的目標函數值。e=0表示優化結果已經超過了函數的估計值或者已聲明的最大迭代次數,e>0表示優化過程中變量收斂于解X,e<0表示計算不收斂。
Matlab處理矩陣運算的強大功能編寫遺傳算法程序有著巨大的優勢,它們結合的原理步驟如下:
(1)編碼:采用二進制編碼方案,用二進制數構成的符號串表示個體,然后隨機產生一個初始種群。
(2)解碼:編碼后的個體構成的種群須經過解碼轉換成原問題空間的決策變量構成的種群,之后才能計算相應的適應值。
(3)選擇與交叉:選擇過程是利用解碼后求得的各個體適應值大小,淘汰一些較差的個體而選擇出一些比較優良的個體,選擇產生的新個體重新配對,形成新的交配對象。
(4)變異:對于二進制的基因串,變異操作就是按照變異概率隨機選擇變異點,在變異點處取反。
2實例分析
針對產銷不平衡問題,核心方法是將產銷不平衡轉換為產銷平衡的情形,然后進行求解。
(1)對于“產>銷”情形:可虛擬一個銷售地(庫存),讓多余的產量均運抵此銷售地,則其銷售量=“產-銷”,同時令該虛擬的銷售地的單位運價為0;
(2)對于“銷>產”,可虛擬一個產地,讓其產量=“銷-產”,同時令該虛擬的產地的單位運價為0。
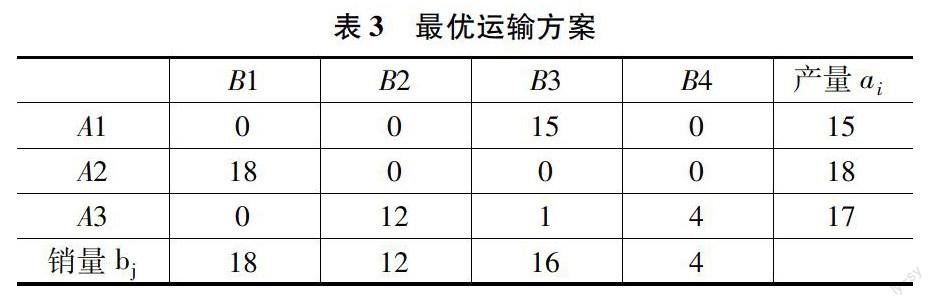
對于這個實際問題,虛設一銷地,令其銷量為產銷量之差:B4=ai-bj=4。該列單位運價為0,即可化為產銷平衡問題。如表1所示。
3結論
在物流運輸中運用Matlab軟件,借助遺傳算法的思想,解決運輸線路的優化問題,簡化了復雜的運輸過程,提高了運輸規劃的效果。且能尋找出物流運輸方案的最優解,從而降低物流成本,使得一些公司在物流上的投資可以進行優化,贏得更多的效益。

