反激開關電源的混沌現象與混沌控制的研究

魏廣平　龍素華

摘 要：混沌主要指出現在確定系統中相關“不確定”現象。而這種“不確定”現象往往發生在非線性系統中。其中開關電源作為一種非線性動力學系統，其特點就是非線性現象比較豐富。另外，在有關參數影響下，開關電源就會出現混沌現象。對此，經過對開關電源的混沌現象進行分析和研究，從而更為全面與深入理解開關電源具備的非線性行為。

關鍵詞：反激；開關電源；混沌現象；混沌控制

單端反激式的拓撲結構具有輸出穩定、輸出波紋小和體積小等特點，因此被大量應用在開關電源相關設計中。對此，從反激式開關電源入手，通過對開關電源相關非線性行為進行研究，制定了混沌有效控制方案，進而可以確保開關電源實現穩定和可靠以及優化運行。

1 應用MATLAB完成數學模型仿真

在研究反激式開關電源離散模型相應混沌現象的過程中，研究方式一般分成定性與定量兩類。其中定性分析方式主要依靠狀態變量頻譜與相圖以及分岔等有效觀察混沌運行現象。而定量分析方式主要包含了Lyapunov指數的分析方式和功率譜的分析方式以及分形維數的分析方式等。在上述分析方式中，利用分岔圖可以清晰的展現出系統處于周期狀態下到混沌狀態的各個流程。而且在分岔圖性方面而言，系統狀態一般情況下是由許多有序點構成。在系統從穩定的狀態慢慢轉換至混沌狀態時，其中參數值的變化，可以利用迭代計算方式獲取數值點，同時各個數值點并非重合，將各個數值點繪制的坐標圖上，就可以充分體現出分岔圖。同時敏感參數嚴重影響著系統的總體運行狀態。若是敏感參數在相應的范圍之內發生變化，就會充分體現出系混沌狀態和周期運行的流程。針對存在混沌問題的非線性系統而言，所有的敏感參數在出現變化時，都會嚴重影響系統的整體運行狀態。可是并非敏感參數的任意排列和組合都造成系統進入混沌狀態。同時系統的混沌狀態僅僅在對應的敏感參數有限的相關范圍之內出現變化。通過上述分析，在電路分析過程中，只可以選取參數可以使系統進入混沌狀態之后，調節系統至小范圍之內的敏感參數變化。

2 創建反激式開關電源的離散模型

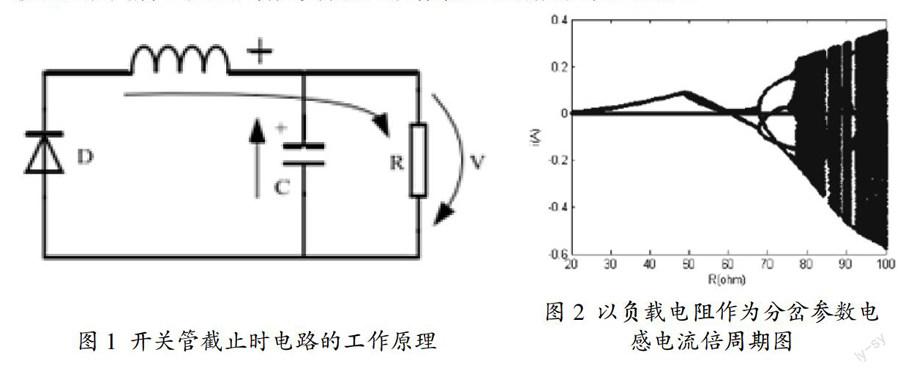
對于反激開關電源而言，高頻變壓器既是變壓器又是儲能電感。一般情況下，可以將電路運行過程分成兩個流程，然后對各個流程完成分析。其中開關管有效連接后，一直到整流二極管截止，此時的高頻變壓器就實施能量的儲存，同時輸出的電眼一般由輸出電容提供。當開關管截止后，整流二級管導通，輸出電壓主要由高頻變壓器（相當于儲能電感）和輸出電容提供。該原理如圖1所示。

以負載電阻當作分岔參數，獲取的圖形如圖2所示。

在MATLB中，利用迭代計算方式對反擊變化器形成的離散映射有關模型進行計算，并且把負載電阻R作為相應分岔參數，該取值的范圍是20Ω至100Ω，而迭代步長是0.1Ω。其它相關電路的參數確定是V1=48V，T=100us，L=0.5mH，C=4.7uF，Vref=20V等。把數值的求解結果合理繪畫在以負載電阻R作為橫坐標、電感電流作為縱坐標的相關坐標平面中，能夠獲取系統分岔圖如圖2所示。從圖中能夠看出，反激變頻器通過周期1和周期2以及周期4等，然后進入了混沌狀態。若是負載的電阻R處在20Ω至100Ω間發生變化，表明系統處于比較穩定周期里。如果負載電阻數值R為45.2Ω，此種狀況下反擊變化器就會產生成倍周期分岔，并且系統就會步入周期2狀態。另外，若是負載電阻數值R為72.8歐姆，此時反激變換器處在周期4狀態。若是負載的電阻數值R逐漸變大，系統最后就會步入混沌狀態。

3 反激變換器的混沌控制

3.1 混沌運動的特點

混沌運動狀態不僅是非周期的，而且運動軌道也是非周期的。簡而言之，對于變量空間而言，混沌吸引子維數通常比周期狀態下的吸引子大，而且混沌運動系統中，所有混沌吸引子每一個對到都為各態遍歷。此種狀況下，混沌可以在對應的混沌吸引子的有關范圍之內，合理控制操作和選取控制目標態，進而確保混沌控制方式具備良好的靈活性。其次，混動運動狀態相應本質特征主要是對初值存在敏感依賴性，所有相鄰的軌道間有關距離會在時間的改變下，通過指數方式變化，從而就造成混沌運動在長期行為下存在不可預見性。對此，在系統中施加相對較小的擾動就能夠使系統運動出現較大變化。

3.2 混沌控制方式

首先是OGY控制方式，其為一項參數微擾先進控制行駛，合理利用混沌運動對于小參數擾動敏感依賴性，可以選擇便于調節敏感參數完成微擾，同時把相關奇異吸子里存在的不穩定軌道實現穩定，進而使被控系統步入固定的周期狀態，實現控制混沌的目標。在設計OGY控制方式的過程中，可是忽視系統相關動力學行為，但必須充分了解系統相圖，選擇有關試驗方法對系統狀態變量實現連續測量，并且計算出系統里閃頻映射，然后建立“龐加萊”截面，確定系統中相關奇異吸引子。并且在確定混沌吸引子相關不穩定周期軌道基礎上，選擇一條可以在混沌吸引子中期望不穩定的周期軌道作為控制目標，同時在混沌運動遍歷運動至該周期周圍時，針對系統此時的狀態變量實現微小擾動，就能夠把混沌的運動穩定在此周期軌道中。其次，參數共振擾法和外加周期的微擾方法。在混沌控制過程中，這兩種方式較為相似，主要為外加周期的微擾信號，其中參數共振的微擾方法一般是干擾動力方程的相應輸入源，然而外加周期的微擾方法一般是微擾系統相應敏感性參數。但是都能夠將混沌有效抑制，并且使系統轉換至期望的周期態。另外，參數共振的微擾方法為一項無反饋型的混沌控制方式，為OGY控制模式中相關改進控制方法。針對敏感參數實現特定頻率的微小擾動，可以有效實現系統混沌狀態轉換至周期運動狀態。即參數振動相應擾動模式可以使動力學系統與之前軌道偏離，并且進入周期軌道。若是施加相應頻率參數擾動，可以使系統慢慢進入某個周期軌道。因此，科學施加參數擾動能夠有效防止系統出現混沌運動，或是消除系統的混沌運動。一般狀況下，選取敏感性參數的過程中，選取對系統狀態的方程影響相對比較大，便于改變狀態變量當作擾動參數。

4 結束語

經過對開關電源的混沌現象進行分析和研究，從而更為全面與深入理解開關電源具備非線性行為，充分應用混沌控制方式，比如說OGY控制方式、參數共振擾法和外加周期的微擾方法等，可以有效確保系統避免或是消除混沌現象。

參考文獻

[1]羅曉曙，汪秉宏，等.DC-DC buck變換器的分岔行為及混沌控制研究[J].物理學報，2013，52（1）：11-17.

[2]張波，曲穎.BUCK DC/DC變換器分岔和混沌的精確離散模型及實驗研究[J].中國電機工程學報，2013，23（12）：99-103.

[3]張波，曲穎.電壓反饋型Boost 變換器DCM的精確離散映射及其分岔和混沌現象[J].電工技術學報，2012，17（3）：43-47.

[4]周宇飛.DC-DC開關變換器的滑模變換結構控制方法及混沌狀態研究[D].廣州：華南理工大學，2011（10）：12-18.