基于線性方程模型的經濟賠償方案的建立

姜妍　劉羽　金晗　張銘升　沈玉波

摘 要：文章結合2014年“深圳杯”數學建模夏令營C題，運用線性方程模型，建立了經濟補償與污染物之間的線性關系。

關鍵詞：線性方程；經濟補償；模型

1 概述

文章結合2014年“深圳杯”數學建模夏令營C題垃圾焚燒廠的經濟補償問題，運用線性方程對經濟補償方案進行求解，其用層次分析法求得的權重作為影響系數，建立了經濟補償與各污染物濃度的線性方程。

2 污染物濃度分析

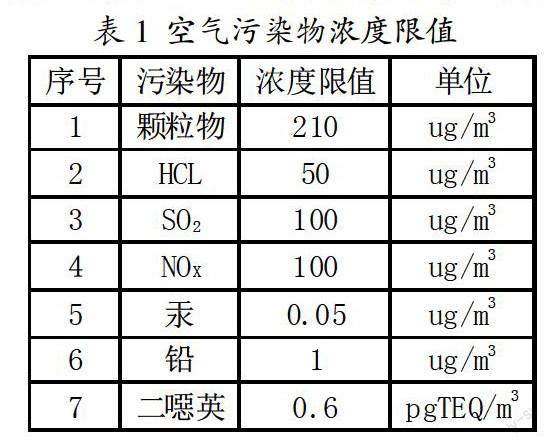
（1）根據我國環境空氣質量標準（GB3095-2012），空氣污染物濃度限值如表1（注：文章中一、二級濃度限值取平均值）。

（2）由上述4、5中模型求得的各污染物在不同地點的濃度和（1）中表1可知，在距離垃圾焚燒廠100m距離之外的污染物濃度遠小于空氣污染物濃度限值（文章中一、二級濃度限值取平均值），但是考慮到時間累積、氣候、風向、空氣濕度等因素的影響，我們在不同地點動態監測的污染物濃度基礎上，乘以一個系數n，作為標準，乘以系數之后，如果污染物濃度大于空氣污染物限定濃度，則根據各污染物濃度進行居民風險經濟補償；反之，如果污染物濃度小于空氣污染物限定濃度，則不賠償。

（3）不同情況下（靜風條件下非沉降性污染物、靜風條件下沉降性污染物，有風條件下非沉降性污染物、有風條件下沉降性污染物）動態監測濃度基礎所乘系數n如表2。

3 線性方程建立與求解

3.1 模型假設

（1）假設居民風險承擔經濟賠償與各污染物濃度呈線性關系；

（2）假設距離污染源每100m進行一個測點，進行經濟賠償；

（3）假設各污染物之間相互獨立。

3.2 相關符號（表3）

3.3 模型建立

則得到居民風險承擔經濟賠償與各污染物濃度的線性方程為：

S=？撞i=1kihj（Ci-Di）mi+P 若Ci

3.4 模型求解

我們選取一個算例（有風條件下距離污染源1000m處經濟賠償金額）進行求解。

已知距離污染源1000m處HCL、SO2、NOX、顆粒物、汞、鉛、二噁英濃度分別為：0.160？滋g/m3、0.256？滋g/m3、0.801？滋g/m3、0.0672？滋g/m3、3.28×10-4？滋g/m3；3.28×10-3？滋g/m3；3.24×10-4？滋g/m3由層次分析法得到的HCL、SO2、NOX、顆粒物、汞、鉛、二噁英系數ki分別為：0.1512、0.1660、0.1647、0.1849、0.1048、0.1013、0.1270。

參考文獻

[1]鄭阿奇，等.MATLAB實用教程[M].北京：電子工業出版社，2005.

[2]李學文，李炳照，王宏洲.數學建模優秀論文（2005-2010）[M].北京：清華大學出版社，2011.

[3]周凱，宋軍全，鄔學軍.數學建模競賽入門與提高[M].浙江：浙江大學出版社，2012.