淺談結構彎矩圖快速正誤分析的方法

摘 要：《結構力學》是工科學生所學三大力學中的最后一門，有一定難度，要學好此門課程除了要具備高等數學、理論力學和材料力學知識外，還要做很多題。其中由等截面直桿組成的結構，其彎矩圖的繪制和檢查是《結構力學》的重點和難點。

關鍵詞：彎矩；桿件；鋼架

《結構力學》是一門連貫性很強的課程，章節之間就像鏈條一樣環環相扣，缺一不可，因此結構內力計算，尤其是彎矩圖的繪制是該門課的重中之重。彎矩圖是否正確，需要進行校核，通常情況應任取多個結點或是桿件為隔離體，將主動力和求好的內力帶入，看是否滿足平衡條件。但是這樣做，一是要多花時間，二是很多人認為多此一舉，因為在求解內力時所用的就是截面法，這樣類似于重復計算。所以很多人不愿意做。結構力學中公式復雜且較多，作者根據多年來的結構力學教學經驗，對最常用的由等截面直桿組成的結構，總結出了一些行之有效的方法，來快速檢查彎矩圖是否正確，從而避免了繁瑣的計算。

1 鉸處彎矩為零

凡是鉸處和自由端（除集中力偶外）彎矩為零，有集中力偶時，該處彎矩值為集中力偶值。如圖1、2所示。

2 結點平衡

結構的剛結點處彎矩值相等（除有集中力偶外），如圖1。我們知道結點要平衡，結點處的兩桿件桿端彎矩一定大小相等，方向相反，同時內側受拉或同時外側受拉。

剛結點處若有集中力偶作用，則從圖上看，結點處的彎矩值不應相等，應相差該集中力偶值。如圖3。

3 固端負彎矩

結構受豎向荷載作用后，固定端會產生負彎矩（上部纖維受拉）或可以理解為桿件受拉側與荷載指向相反。如圖4中A、B端的彎矩與荷載方向相反。

4 傾向性分析

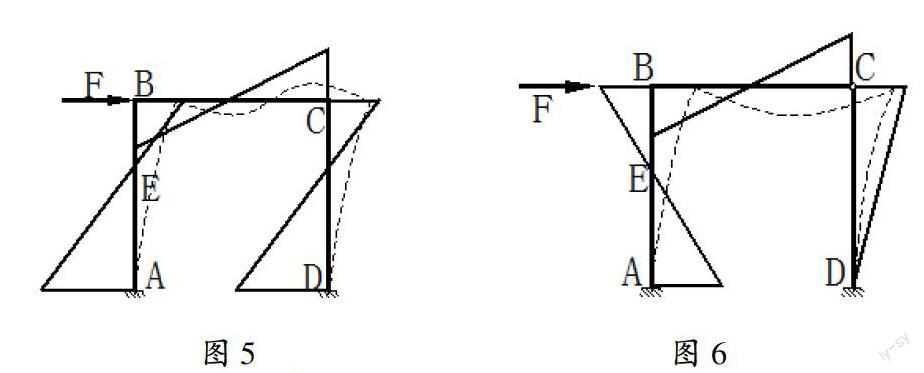
桿件的彎矩圖與桿件受力后的變形相一致。（或可以理解M圖斜率與桿件受力后的傾斜一致）如圖5，其中虛線為結構的變形。如圖6顯然錯誤。聯系上幾個規則，我們可以看出：剛結點B沒有結點平衡；AB桿彎矩傾向性錯誤；鉸C處彎矩應為零；D點應該有固端負彎矩。

5 過鉸不變原則

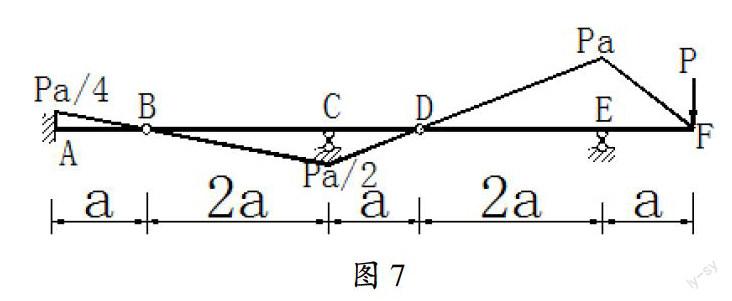
彎矩穿過鉸，若未受到任何荷載作用則斜率不便，直至遇到荷載才變。利用這一點我們可以很快速的繪制一些結構彎矩圖，如圖7。

6 微分關系

其實這一點已經不是什么新鮮的了，教材上都有，只不過學者們做完題后，總是忘了用它來檢驗計算結果。這里就彎矩與荷載的關系而言有：（1）無荷載段M為（斜）直線，如圖5、7等。（2）有集中力處M有尖點，如圖4、7，（支座反力也可以看作集中力）。（3）有均布荷載段，M成二次拋物線。如圖2等。（4）有集中力偶兩側彎矩有突變，突變值即為集中力偶值，如圖1、3等。這是計算中非常適用的判斷依據。

7 平衡力系問題

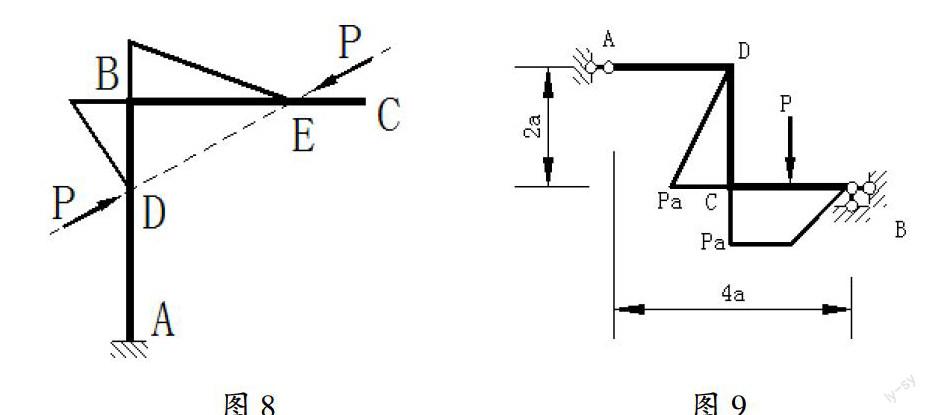
如果有一平衡力系作用在某一幾何不變的部分時，則只有該部分有內力和反力（DBE段），該部分以外沒有任何內力和反力。如圖8。

8 直鏈桿問題

若某桿件支座端為一可動鉸支座鏈桿且指向桿軸，且該桿未受任何橫向外力作用，則該桿彎矩為零。如圖9的AD桿。

綜上所述，只要將這八點牢牢掌握，則不僅可以簡化計算、提高計算速度，更重要的是可以快速檢查彎矩圖的正誤。除此之外，對于靜定結構中，荷載作用在附屬部分和作用在基本部分上受力的異同，文章就不再冗述。

參考文獻

[1]龍馭球，包世華.結構力學[M].北京：高等教育出版社，1999.

[2]高健.建筑力學[M].黃河水利出版社，2009，6.

作者簡介：白建昆（1977，12-），男，籍貫：昆明，學歷：研究生，職稱：工程師，從事工作：建筑工程。