波動方程非線性傳播仿真

孟艷

【摘要】波動方程是波動傳播過程中，介質中各個質點振動物理特性的數學描述。非線性作用是介質的一種固有屬性，與衰減作用類似，在波動傳播的過程中改變波源的振動波形。通過對波動方程的非線性仿真，為進一步的研究波的非線性特性提供了基礎

【關鍵詞】波動方程 非線性 仿真

一、引言

非線性現象是指波在傳播過程中，產生波源整數倍的高次頻率，非線性是傳播介質的基本特性。 本文以三維Westervelt波動方程為基礎， 利用其時間域有限微分解， 通過計算機仿真的方式，完成對波動場內任意點的波動仿真， 為仿真研究非線性特性提供基礎。

二、非線性波動方程的數值解

常見波動方程都是非常復雜的偏微分方程，其中聲場描述參數聲壓p是一個與時空都有關系的物理量，在笛卡爾坐標系下可以表示為：P（x，y，z，t）。時域有限微分法的基本思想是使用微分替換方程中的導數，將未知的時間空間變量用已知時間或者空間變量表達。通過不斷的重復，計算時間和空間上未來的結果。

為了研究方便，我們首先將Westervelt方程在一維坐標下展開化簡為僅含對p的偏導數，其中拉普拉斯算子定義為空間的偏導數：

對于 的導數，代入Westervelt方程得到：

上式中包含壓強P在時間和空間上的偏導數，在時間t區間內，振動的函數。每個坐標點 代表了t時刻，x軸上的坐標點i的壓強。 的一階導數表示為：

使用上面的微分形式替換導數形式，可以獲得 的精度，其中h為時間或空間的步長。上面兩個公式中時間和空間步長都為1。從上面的兩個公式可以化解出：

從上面兩個公式可以看出，空間上點i+1在時間t的值可以通過上一空間點（i-1）以及點i處的導數獲得。在給定初始條件 條件下，使用前一個公式在x軸方向上計算下一個坐標位置的值，使用后一個公式計算t+1時刻的坐標值，這樣在x-t平面延伸，最后獲得x軸方向上，t時間區間內，所有的點的壓強。

三、仿真結果

從公式可以看出，非線性系數和液體黏滯系數分別作用到不同的壓強分量上，我們可以將β與η分別設置為0來研究衰減和非線性對波動傳播的影響。

首先我們以人體組織介質的物理參數值作為模擬的基礎，假設x方向的長度為200 ，在100 處放置一個振源，振源的激勵波為：

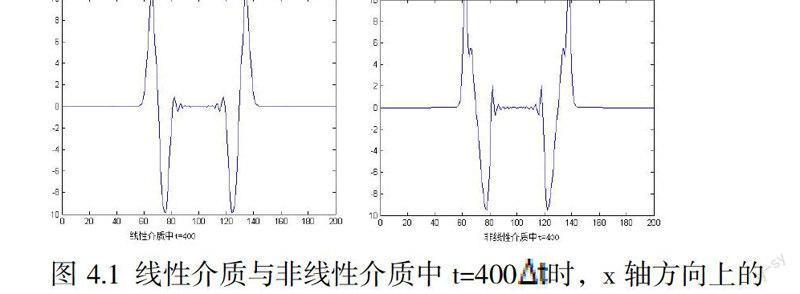
我們首先假設介質黏滯系數η及非線性系數β都為0，使用FDTD計算波動在x軸方向傳播。經過400 時刻后，x軸方向上質點的振幅如圖4.1所示：

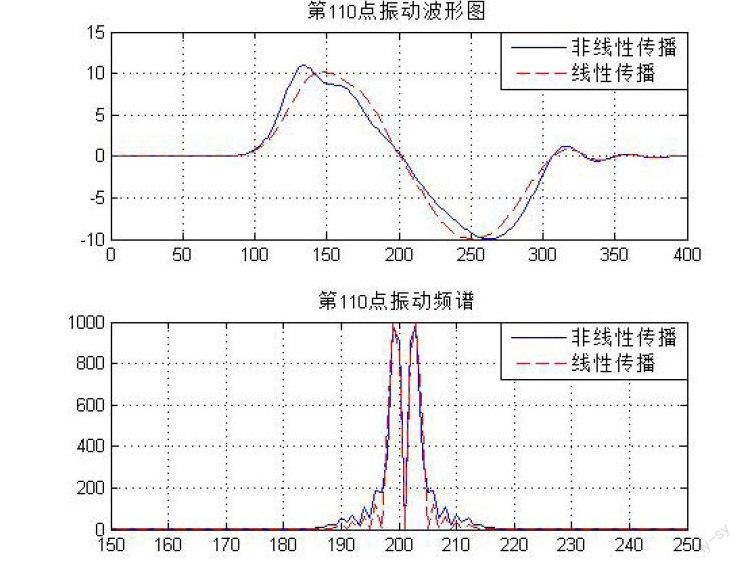
對比圖4.1中波形可以看出，在線性介質中，波動波形能夠保持振源振動波形的光滑特性，但是，在非線性介質中，質點壓縮周期的斜率高于線性作用下的傳播。下面，我們對比非線性介質與線性介質中，距離振源長度為10 和20 處，質點在[0，400 ]時間周期內，振動的波形曲線和頻譜曲線。

線性介質中傳播的質點先到達最大距離。由于距離的導數是速度，那么，從振動曲線的斜率可以看出質點在對應時間區間內振動的速度。也就是說，在非線性介質中，時間區域[100，150]，[250，350]內，質點振動速度大于線性介質。這與非線性產生的物理解釋完全吻合。

【參考文獻】

【1】J.F.Greenleaf Measurement of the acoustic nonlinearity parameter B/A in human tissue by a thermodynamic method. The Journal of the Acoustical Society of America， vol. 76， no4， pp. 1023-1029

【2】V. P. Kuznetsov， “Equations of Nonlinear Acoustics，” Sov. Phys. Acoust. 16， 467-470.

【3】Y.-S. Lee， "Numerical solution of the KZK equation for pulsed finite amplitude sound beams in thermo viscous fluids，" Ph.D. dissertation， The University of Texas at Austin

【4】凌濤 ，鄭海榮，“超聲造影微泡非線性聲學特性與成像研究進展”中國介入影像與治療學2009年第6卷第4期 p392～p396

【5】TL SZABO Diagnostic Ultrasound Imaging Inside Out，Appendix B