鐵路軌檢車軸箱振動特性分析

肖 乾，方 駿，譚祖賓，袁其剛

(1 華東交通大學 現代軌道車輛研究所，江西南昌330013; 2 南車洛陽機車有限公司，河南洛陽471002)

鐵路軌檢車軸箱振動特性分析

肖 乾1，方 駿1，譚祖賓2，袁其剛2

(1 華東交通大學 現代軌道車輛研究所，江西南昌330013; 2 南車洛陽機車有限公司，河南洛陽471002)

軸箱是輪對與構架既相互連接又相互運動的關鍵部件，它起著承上啟下的關鍵作用。鐵路軌檢車主要用于鋼軌探傷，探傷設備的固定支架一般與軸箱相連，因此研究鐵路軌檢車軸箱振動特性對于提高探傷設備的使用壽命和探測精度具有重要意義。針對某型號軌檢車建立整車車輛動力學模型，在此基礎上建立了運動方程，得到車輪—軸箱系統頻率響應輸出;結合Hypermesh和Abaqus軟件建立有限元模型并利用Block Lanczos算法進行了模態分析，得出軸箱前六階的固有頻率和主振型，得到第一階模態固有頻率為637.26 Hz;使用SIMPACK動力學軟件建立軌檢車動力學仿真模型，使軌檢車在定義有激勵的直線軌道上以70 km/h的速度行駛，計算出軌檢車的車輪—軸箱系統垂向和橫向頻率響應輸出并得出其共振頻率，得到橫向和垂向振動共振頻率分別為20 Hz和63 Hz。可以發現第一階模態固有頻率遠遠大于其共振頻率，因此軸箱的結構設計合理，在其工作速度范圍內是安全的。

軌檢車;軸箱;振動特性;模態分析

鐵路軌檢車主要用于鋼軌探傷，探傷設備的固定支架一般與軸箱相連，因此，軸箱的振動特性將直接影響探測精度。另外，軸箱的振動特性對于列車懸掛裝置選型及其自身結構優化也有非常重要的參考作用。軸箱振動特性研究一般通過動力學仿真或實際跟車檢測兩種方式進行，任尊松［1］等在車輛上布置加速度傳感器［2］獲得了武廣客運專線高速動車組車輛軸箱、構架以及車體振動加速度曲線圖，給出振動加速度功率譜密度計算方法。研究結果表明，與列車運行速度和車輪半徑對應的輪軸轉動頻率在輪對、構架和車體振動中均有明顯體現;列車運行速度越高系統振動加速度峰值越大，通過道岔時可激起車輛系統振動幅值更大的振動。劉楠［3］等利用有限元分析軟件ANSYS對軸箱結構進行了靜強度與模態分析，獲得了軸箱結構的固有頻率和振型，為了解結構的薄弱環節、動態性能評定及結構綜合強度性能的評定提供依據。因此了解軸箱在特定激勵的軌道上的振動特性和固有頻率、主陣型，避免車輪—軸箱系統垂向和橫向振動頻率接近軸箱固有頻率，對于保證探傷設備的探測精度具有重大意義。

1 軸箱動力學分析模型

強迫振動分析有兩種不同的方法，時域分析法和頻率分析法［4-5］。時域分析法所求的是系統的瞬態響應，需要用到數值積分，這種方法很容易處理系統的非線性特性。頻域分析法所求的是系統對不同頻率干擾的穩態響應，所得到的是系統的頻率響應函數，優點是計算速度快，計算結果的分析也比時域法簡單。根據軌檢車的結構、裝配特點建立動力學分析模型如圖1所示，該模型由車體，轉向架，車輪—軸箱系統，一系懸掛，二系懸掛組成。

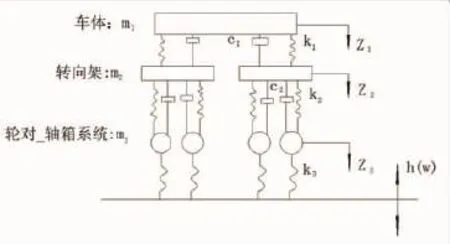
圖1 完整的車輛動力學模型

圖1中m1是車體質量;m2是轉向架的質量;m3是車輪對—軸箱質量;K1，C1是二系懸掛的垂向剛度和阻尼; K2，C2是一系懸掛的垂向剛度和阻尼;K3是輪軌等效線性接觸剛度［6］。軌檢車的參數如表1和表2所示。

表1 軌檢車質量參數

表2 軌檢車懸掛參數

懸掛參數剛度/(MN·m－1) 阻尼/(kN·S·m－1)一系縱向 12 6一系橫向 10 6一系垂向 0.6 6二系縱向 0.15 60二系橫向 0.15 60二系垂向 0.45 80

建立車輛系統運動方程為:

式中M為系統質量矩陣，C為系統阻尼矩陣;K為系統剛度矩陣;Z為位移矢量，Z=(Z1Z2Z3)T;Ft為來自于軌道的垂向干擾力矢量;Ft=F(w)=TTkKh(w)，其中h(w)，為線路干擾矢量;TTk為系統剛度關聯矩陣的轉置矩陣。

根據上面所述條件求解車輛系統運動方程(1)得到系統頻率響應方程(2):

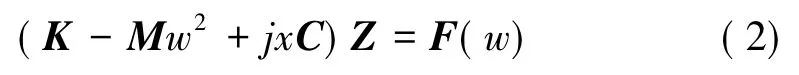
得到Z=(Z1Z2Z3)T，其中Z3為輪對—軸箱頻率響應輸出。

2 軸箱的振動特性求解

SIMPACK是機械系統動力學性能仿真分析軟件，可以描述并預測復雜機械系統的運動學及動力學性能，可以分析其系統振動特性，受力狀況以及零部件的運動位移、速度、加速度等［7］。利用動力學軟件SIMPACK和動力學模型(如圖1)建立軌檢車整車動力學仿真模型如圖2所示。軌檢車模型參數如表1和表2所示，車輪名義滾動圓直徑920 mm，車輪踏面為標準踏面S1002;軌距為1 435 mm。

圖2 在SIMPACK中建立的車輛模型

建立車輛動力學模型時，為了更加真實模擬實際情況，研究輪軌之間的相互作用，特別是為了準確預測和分析車輛的動態響應，須要定義軌道激勵［8-9］，軌道隨機激勵是引起車輛系統產生各種動態響應的主要原因。SIMPACK軟件主要提供兩種軌道激勵(Track Excitation and Rail Excitation)，其中軌道不平順是軌道激勵之一，本次建模選擇的是相對于軌道的類型，軌道不平順選用的美國五級軌道譜，五級軌道譜密度函數表達式如式(3)所示［10］:

其中Sv(Ω)為譜密度，cm2·m/rad;Ω為空間波數，rad/m。

在SIMPACK前處理中，建立了車輛模型和定義了軌道激勵，在車輪參考坐標系上定義傳感器，使其在10 000 m直線軌道上以70 km/h行駛，可以計算出車輪—軸箱橫向加速度和垂向加速度隨時間的變化情況如圖3和圖4所示。

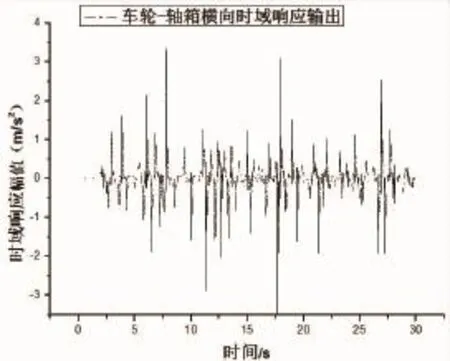
圖3 車輪—軸箱橫向加速度時域響應輸出

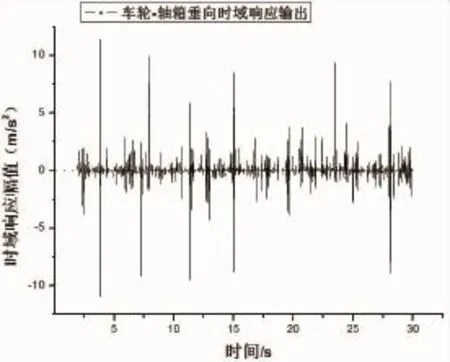
圖4 車輪—軸箱垂向加速度時域響應輸出

在上述兩條曲線基礎上可以得到車輪—軸箱系統橫向和垂向頻率響應輸出，也能得到橫向和垂向共振頻率如圖5和圖6所示。

圖5 車輪—軸箱橫向頻域響應輸出

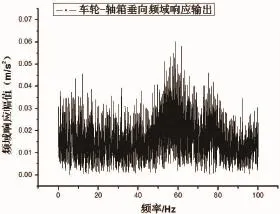
圖6 車輪—軸箱垂向頻域響應輸出

將車輪與軸箱作為一整體對象，計算出如上圖所示的車輪—軸箱時域響應輸出和頻率響應輸出。從圖3和圖4可以知道橫向和垂向時域響應輸出在開始階段波動比較劇烈，但是隨后呈衰減趨勢，直至列車運行平穩。圖5和圖6中表明車輪—軸箱系統橫向振動共振頻率約為20 Hz，垂向振動共振頻率約為63 Hz。并且橫向頻率響應幅值在0～20 Hz比較大，垂向頻率響應幅值在0～100 Hz范圍內呈現極大值，這個極大值點就是共振頻率。

3 軸箱模態分析

將軸箱模型導入網格劃分軟件Hypermesh［11］中劃分網格。因為軸箱體形狀比較復雜，所以在建立有限元模型時，對軸箱體采用四面體單元C3D4對結構進行離散，得到軸箱體有限元模型如圖7所示。

建立有限元模型后，導入Abaqus中，利用Block Lanczos算法進行模態分析。網格劃分的精度直接關系到有限元計算的準確性，網格劃分力求幾何形狀與原結構一致，并采用疏密相結合的方式，軸箱裝配體共離散成64 290個節點，261 635個單元。

圖7 軸箱體有限元模型

模態分析的最終目標是識別出系統的模態參數，為結構系統的振動特性分析、振動故障診斷和預報以及結構動力特性的優化設計提供依據［12］。通過Abaqus模態分析得到前6階模態，得到相應固有頻率和主陣型如圖8和表3所示。

軸箱第1階頻率是637.26 Hz，軸箱體軸承孔繞X軸扭轉變形，第2～6階頻率為1 090.5～1 778.7 Hz，軸箱體軸承孔和兩只吊耳都發生變形，兩只吊耳繞X軸扭轉變形第1階頻率為1 485.9 Hz，軸箱底部也發生微小變形。

如果模態分析結果與車輪－軸箱系統橫向和垂向頻率響應輸出的結果進行對比，可以發現，橫向共振頻率和垂向共振頻率沒有出現在軸箱模態中，并且第1階模態遠遠大于上述兩個頻率?？梢灾涝撥墮z車軸箱結構設計較為合理，保證了測量儀器的精度，使軸箱的共振頻率遠遠偏離第1階固有頻率。

圖8 軌檢車軸箱前6階陣型

表3 軌檢車軸箱模態

4 結論

(1)在Abaqus中給軌檢車振動模態施加邊界條件計算后，軸箱第1階頻率是637.26 Hz，軸箱體軸承孔繞X軸扭轉變形，第2～6階頻率為1 090.5～1 778.7 Hz，軸箱體軸承孔和兩只吊耳都發生變形，兩只吊耳繞X軸扭轉變形第一階頻率為1 485.9 Hz。

(2)在動力學軟件SIMPACK中建立車輛模型，計算表明:車輪—軸箱系統橫向振動共振頻率約為20 Hz，垂向振動共振頻率約為63 Hz。如果將該結果與軸箱振動模態的計算結果進行對比，可以發現上述2個頻率沒有出現在軸箱模態中，并且第1階模態遠遠大于上述兩個頻率。

(3)通過上述分析知道該軌檢車軸箱結構設計較為合理，保證了測量儀器的精度，軸箱的共振頻率遠遠偏離第1階固有頻率，在第6階模態時，軸箱兩只吊耳繞X軸反向扭轉變形，軸箱底部也發生微小變形。為增大軸箱底部剛度，可以在底部兩只吊耳處分別增加兩桿，連接吊耳底部和軸箱底部。

［1］ 任尊松，劉志明.高速動車組振動傳遞及頻率分布規律［J］.機械工程學報，2013，49(16):1-7.

［2］ 何聲漢，林建輝，張兵.高速列車軸箱振動無線采集器［J］.工程與實驗，2010，50(1):54-57.

［3］ 劉楠，傅茂海，金鑫，王平.機車車輛軸箱結構靜強度與模態分析［J］.機械制造，2013，43(3):17-23.

［4］ 陸冠東.車輛系統動力學計算方法研究［M］.北京:中國鐵道出版社，2011.

［5］ 倪振華.振動力學［M］.西安:西安交通大學出版社，1988.

［6］ 陳果，翟婉明，蔡成標，王其昌.傳統車輛模型與車輛－軌道耦合模型的垂向隨機振動響應分析及比較.［J］.鐵道學報，1999，21(5):70-73.

［7］ 王晨，羅世輝，馬衛華，劉韋，方翁武.直線電機懸掛結構的振動特性分析［J］.鐵道機車車輛，2013，33(4):66-70.

［8］ 李增光，吳天行.浮置板軌道參數激勵振動研究［J］.振動與沖擊，2010，29(2):17-21.

［9］ 陳伯靖，錢小益，秦超紅，李成輝.鐵路鋼軌受力分析模型比較研究［J］.工程力學，2013，30(6):93-97.

［10］ 翟宛明.車輛一軌道耦合動力學(第3版)［M］.成都:科學出版社，2007.35-42.

［11］ 周新建，王若飛，等.基于Hypermesh的立式加工中心立柱結構的拓撲優化［J］.華東交通大學學報，2013，30(6):78-83.

［12］ 魯寨軍，田紅旗，周丹.270 km/h高速動車模態分析［J］.中國鐵道科學，2005，26(6):18-22.

Axle-box Vibration Characteristic Analysis for a Railway Track Inspection Vehicle

XIAO Qian1，FANG Jun1，TAN Zubin2，YUAN Qigang2
(1 Institute of Modern Railway Vehicles，East China Jiaotong University，Nanchang 330013 Jiangxi，China; 2 CSR Luoyang Locomotive Co.Ltd.，Luoyang 471002 Henan，China)

Axle-box is the key components of mutual connection and movement between wheel and frame.Railway track inspection vehicle is mainly used for rail flaw detection，and fixed bracket of inspection equipment are commonly connected to the axle-box，so vibration characteristic analysis is of great significance for improving the service life and detection precision of a flaw detection equipment.The dynamics model of the vehicle was established for one type of vehicle，and then the equation of motion was established and solved on this basis.The finite element model was set up by combination of Hypermesh and Abaqus，and Block Lanczos algorithm was used for the modal analysis.It obtained first six order natural frequency and main modes of the axle box.The first order modal natural frequency was 637.26 Hz.Vehicle dynamics simulation model was established by using SIMPACK.The inspection vehicle was driven at the speed of 70 km/h in linear orbit defining incentive.Vertical and horizontal frequency response output and its resonant frequency of wheel axle-box system were obtained respectively as 20 Hz and 63 Hz.It＇s found that the first order modal natural frequency is far greater than its resonant frequency，so the axle-box structural design is reasonable and safe within the scope of the work speed.

Inspection vehicle;Axle-boxes;vibration characteristics;modal analysis

U216.61

A

10.3969/j.issn.1008－7842.2015.02.03

1008－7842(2015)02－0010－04

)男，副教授(

2014－11－03)