生化參數對耦合回路的影響

鄭赟　孔唯旺

摘 要：網絡組成的互連元件之間具有復雜的動態行為。一些子網通常被視為他們的特殊功能的網絡模塊。反饋回路在這些網絡圖案中發揮的重要作用。通過改變一個參數值，我們發現，耦合回路可以表現出豐富的動力學行為。我們通過分岔圖分析兩個耦合結構的動力作用，我們找出了耦合系統發生hopf分岔時的hill系數的區間和發生雙穩態的時的壓制參數的區間。

關鍵詞：hill系數 耦合回路 壓制參數 hopf分岔 雙穩態

中圖分類號：TP211 文獻標識碼：A 文章編號：1674-098X（2015）04（c）-0008-05

Abstract：Network consisting of the complex between the interconnection elements may have a complex dynamic behavior.Some subnet usually is regarded as a network of their special function module.Feedback loop play important role in these network motifs in the.By changing the value of a parameter， we find that， the coupling loop can exhibit rich dynamic behavior. We analyze the dynamic action of two coupled structure by means of the bifurcation diagram，we find the parameter interval of Hill coefficient when Hopf bifurcation occurs and the range of suppression parameters state when the bistability occurring.

Key Words：Hill Coefficient；Coupling Loop；Compaction Parameters；Hopf bifurcation； Bistability

眾多的細胞內或細胞外的生物分子之間復雜的相互作用本質上總是存在的。正是由于這些相互作用，細胞的復雜行為可以很容易找到，如雙穩態[1-3]，振蕩[ 4-5 ]等其他的動力學行為。

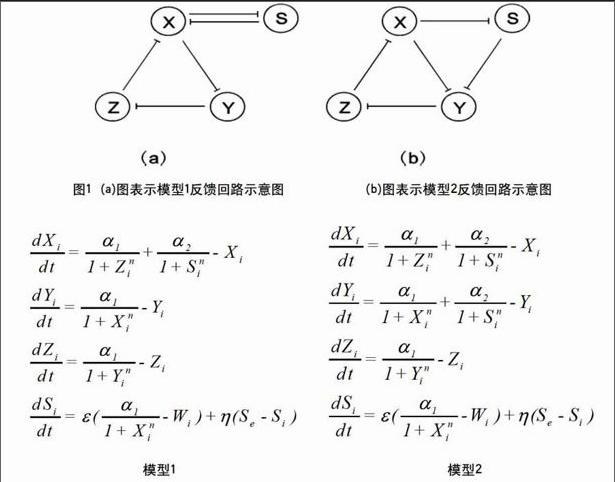
耦合反饋回路由一個中心負反饋回路和一個額外的反饋回路，根據拓撲知識可知，這樣的耦合反饋回路共有12種情況[6]，為了更加方便的考慮生化參數對耦合系統的影響，在這里只考慮12種耦合反饋回路中的2種，這里稱為模型1和模型2，其中模型1用于考慮hill系數變化對耦合反饋回路的影響，模型2用于考慮壓制參數對耦合反饋回路的影響。

生化參數對其他類型的耦合系統的影響已經得到了一些較為有用的結果，例如hill系數對壓制振子耦合系統的影響[7]；細胞個數對耦合系統的影響[8-10]；以及對耦合系統群里感應的影響[11-12]；改變生化參數導致的振動死亡[13]。

該文主要關注hill系數對模型1耦合反饋回路的動力學影響和壓制參數對模型2耦合反饋回路的動力學影響。利用分岔分析和數值模擬，發現當hill系數在一定范圍時，模型1耦合系統在隨著密度Q的增大，會由穩定的同質平衡態變成周期1振動，當hill系數小于或者大于一定范圍值時，耦合系統將會一直處于穩定的同質平衡態的動力學狀態。對于模型2神經網絡的反饋回路，雙穩態動力學現象是發生在較小的參數區間。即當抑制參數在區間[3.1， 3.3]內取值時，系統才會出現雙穩態。

1 數學模型

這里將會用2個模型進行分析，2個模型都是一個負反饋回路三者加上一個額外的反饋回路，2個模型中相同的負反饋回路稱為中央反饋回路，并且是由X，Y，Z3個蛋白質組成，X，Y，Z是由基因x，y，z生成的蛋白質，模型1在中央反饋回路中X上添加了與S的相互壓制的正反饋回路，模型2是在中央負反饋回路中X上添加了對S的壓制且S對Y的壓制。這樣就在中央反饋回路上添加了X，Y，S組成的前饋環。

模型1主要用于對分析hill系數的變化對耦合系統的動力學的影響，而模型2是主要用于抑制參數對耦合系統的影響模型之間通過群體感應機理耦合而構成多細胞系統，其中信號分子可以擴散到群體中每一個細胞的內部，并調控目標基因的表達。合并轉錄、翻譯過程為單步過程，并采用擬平衡態假設，來建立數學模型，由此得到如下多細胞系統模型。

參數為hill系數，無量綱參數和表示最大調控速率，參數描述時間尺度分離，擴散系數描述細胞膜對信號分子的滲透性。注意到：利用擬平衡態假設，其中代表細胞密度，在恒化器實驗中通過改變整個恒化器的體積可以控制在0到1之間變化，我們的主要目的在于分析hill系數是n和最大調控速率如何影響多細胞系統的協作行為，應用Matlab和Xppaut進行分析。其他參數被固定如下：

模型1：；

模型2：。

2 hill系數n對耦合系統動力學的影響

這里主要考慮的是模型1振子的耦合系統，以細胞密度作為分岔參數，做關于的分岔圖。首先考察當hill系數n≤2.3時對耦合系統動力學的影響。見圖2（a），從分岔圖中可以看到耦合回路系統處于穩定的同質平衡態。下面考慮hill系數n≥2.4時，耦合系統的出現了什么變化，從以細胞密度作為分岔參數，做關于的分岔圖，從圖2（b）中可以看出，當hill系數n=3時，在時，耦合系統還是穩定的同質平衡態，當時，出現Hopf分岔，圖像2（b）中紅色粗線段代表穩定的同質平衡態，藍色虛線段代表不穩定狀態，綠色虛實線段代表系統處于周期1振動狀態。當hill系數n≥3.1時，可以從圖2（c）中看出，耦合系統又處于同質平衡態，出現與圖2（a）相同的動力學現象。根據3個分岔圖像可以得出當hill系數2.4≤n≤3.1時，耦合系統在隨著密度Q的增大，會由穩定的同質平衡態變成周期1振動的動力學現象，當hill系數不取區間[2.4，3.1]值時，耦合系統將會一直處于穩定的同質平衡態的動力學狀態。endprint

3 抑制參數對耦合系統的影響

這里主要是用模型2振子的耦合系統進行分析，還是以細胞密度作為分岔參數，做關于的分岔圖。首先考察當抑制參數時對耦合系統動力學的影響，根據分岔分析，由圖3（a）可知，耦合系統系統是一直處于穩定的同質平衡態，故可知當對抑制程度較低時，耦合系統將會處于穩定的同質平衡態，再考慮當對抑制程度提高到一定程度時，即當抑制參數滿足條件時，根據圖3（b）的分岔圖可知，耦合系統出現了雙穩態的動力學現象，即細胞密度在[0.9272， 0.9629]取值時，耦合系統會場出現雙穩態現象，最后考慮抑制參數時，此時對抑制程度提高到很大，且在具有生物意義的范圍以內，由圖3（c）可知，耦合系統又處于穩定的同質平衡態。

4 結論

在這篇文章中，主要了耦合反饋回路的動力學行為。耦合反饋環被認為是由一個中央負反饋回路加上另一個額外的反饋回路。通過改變hill系數和抑制參數的取值，并隨著XPPAUT和MATLAB的幫助，為這2個系統得到了分岔圖。通過數值分析，發現發生振蕩是在模型1耦合回路系統，且是通過Hopf分岔。只有2種動狀態：振蕩和穩定狀態。且要求hill系數在區間[2.4， 3.1]內取值時，耦合回路系統才能發生振蕩。對于模型2神經網絡的反饋回路，雙穩態動力學現象是發生在較小的參數區間。即當抑制參數在區間[3.1， 3.3]內取值時，系統才會出現雙穩態。

該文用了2個模型進行了分開的討論，模型在幾個方面進行了簡化。首先，沒有考慮詳細的生物過程，把轉錄、翻譯、啟動子結合等過程合并成了一步，并且沒有考慮組合調控的效果；其次，忽略了一些生物因素，如細胞的多樣性，基因表達過程中固有的隨機漲落，信息傳輸過程中的時間滯后，轉錄因子協作性的效果等等。這些方面對耦合系統動力學現象的影響以及在一個耦合回路系統中同時對這兩個生化參數的討論需要進一步的研究。

參考文獻

[1] J.J.Tyson and H.G.Othmer， The dynamics of feedback control circuits in biochemical pathways，Progr.Theor. Biol. 1976，5：1-62.

[2] A.D.Keller，Model genetic circuits encoding autoregulatory transcription factors，J.Theor. Biol.1995，172：169-185.

[3] R. Thomas，D.Thieffry and M. Kaufman， Dynamical behaviour of biological regulatory networks，Bull. Math.Biol，1995，57：247-276.

[4] K.Pye and B. Chance， Sustained sinusoidal oscillations of reduced pyridine nucleotide in a cell-free extract of Saccharomyces carlsbergensis， Proc.Natl.Acad.Sci.USA， 1996，55： 888894.

[5] B.Hess and A.Boiteux， Oscillatory phenomena in biochemistry.Annu.Rev. Biochem，1971，40：237-258.

[6] CHEN Aimin，WANG Xingwang，LIU Caixia，WANG Junwei，Coupled Feedback Loops Form Birhythmicity and Inhomogeneous Limit Cycles of Synthetic Regulatory Networks， proceeding of the 32nd Chinese control confeience， 2013.

[7] I. Potapov，E. Volkov， Dynamics of coupled repressilators： The role of mRNA kinetics and transcription cooperativity[J].PRE ，2011，83：031901.

[8] Qizhi Yi，Tianshou Zhou.Communication-induced multistability and multirhythmicity in a synthetic multicellular system[J].PRE，2011，83：051907.

[9] 易奇志，杜焰，周天壽，系統規模對群體行為的效果[J]，物理學報，A Sin.2013，62（11）：544-533.

[10] Q.Z.Yi，J.J.Zhang，Z.J.Yuan，etal Collective dynamics of genetic oscillators with cell-to-cell communication：a study case of signal integration[J].Eur.Phys.J.B，2010，75（3）：365-372.

[11] D.Yang，Y.Li，A.Kuznetsov. Characterization and merger of oscillatory mechanisms in an artificial genetic regulatory network[J].CHAOS，2009，19（3）：033115.

[12] A.Koseska，E.Ullner，E.Volkov ，J.Kurths，er al.Cooperative differentiation through clustering in multicellular populations[J]. Journal of Theoretical Biology， 2009，263（2）：189-202.

[13] A. Koseska，E.Volkov，J. Kurths.Detuning-dependent dominance of oscillation death in globally coupled synthetic genetic oscillators[J]. EPL，2009，85：（2）.endprint