基于波形捷變的多傳感器機動目標跟蹤

盛 丹,王國宏,張翔宇

(海軍航空工程學院信息融合研究所,山東煙臺264001)

基于波形捷變的多傳感器機動目標跟蹤

盛 丹,王國宏,張翔宇

(海軍航空工程學院信息融合研究所,山東煙臺264001)

針對現代戰場中目標往往采用機動方式運動的情況,為了提高目標跟蹤的準確性和精確性,結合多傳感器數據融合的優點,提出了一種基于波形捷變的多傳感器機動目標跟蹤方法。該算法通過波形捷變來改變量測的精度。首先在現有文獻的基礎上,將波形捷變方式推廣到二維空間,把雷達量測的克拉美羅下限(Cramer-Rao lower bound,CRLB)近似為量測誤差協方差,由于該CRLB是關于發射波形參量的,從而把雷達跟蹤的信號處理與數據處理結合在一起,通過波形參量的動態選擇得到量測誤差協方差的最小值。從而在整個雷達跟蹤過程中提高信噪比(signal to noise ratio,SNR),降低量測誤差。其次,在數據處理上,采用多傳感器數據融合及粒子濾波進一步提高機動目標跟蹤的精度。最后,將該算法與傳統的Kalman濾波、粒子濾波及只對一維空間的量測采用波形捷變的算法和交互多模型方法(interacting multiple model,IMM)進行仿真比較,仿真結果顯示該算法對機動目標的跟蹤精度顯著提高。

波形捷變;機動;多傳感器;克拉美羅下限

0 引 言

機動目標跟蹤由于其復雜性、隨機性和多樣性成為目標跟蹤領域研究的熱點和難點,國內外眾多學者致力于研究有效的機動目標跟蹤算法。目前的研究主要集中在目標的運動模型和濾波算法的研究,常用的模型有多模型(multiple model,MM)、交互多模型(interacting multiple model, IMM)、切換模型等。在多模型基礎上,Shalom提出了交互式多模型方法,這一方法對無序目標的機動檢測顯示了更好的魯棒性和跟蹤的穩定性。目標機動時其運動模型和觀測模型通常是非線性的,常用的濾波方法有擴展卡爾曼(extended Kalman filter,EKF)、不敏卡爾曼(unsensitive to Kalman,UKF)、粒子濾波(particle filter,PF)等,其中,粒子濾波由于不受系統非線性非高斯的約束,已成為研究的熱點。盡管現已有的這些研究都取得了一定的成效,但是大多數方法只是從數據處理方式上尋求最優的效果。而目標的跟蹤精度不僅與數據的處理方式相關,也受信息的處理方式的影響,比如發射信號的波形及其參量的選擇、回波信號的處理方式等。因此把信號處理和數據處理相結合是當前提高跟蹤精度的研究方向之一。隨著傳感器技術及數字波形產生器的發展,自適應波形設計及調制也得到越來越多的應用[45],波形捷變傳感器就是通過控制發射信號的波形或其參量來適應目標和周圍環境。因此可以提高傳感器的各項性能,如減小跟蹤誤差、提高檢測概率、提高識別精度及提高傳感器的利用效率等。文獻[6-7]討論的是一維空間沒有雜波的情況下,跟蹤水下目標時波形的動態選擇及設計。目標的運動模型和觀測模型均假設為線性,通過波形的最優設計和參量選擇實現了跟蹤均方誤差的最小化。在文獻[8]中該方法與概率數據互聯相結合,實現了雜波存在下的目標跟蹤。此后,Sira等人對波形捷變進行了一系列的研究,研究對象仍是水下目標[914]。文獻[9]把兩部聲納的量測直接合并成新的量測,然后建立量測誤差的克拉美羅下限(Cramer-Rao lower bound,CRLB)方程,通過動態選擇波形的參量來尋求量測誤差協方差的最小值,從而提高跟蹤精度。文獻[10]給出3種調制波形,建立量測誤差的CRLB方程,同時對波形及波形的參量進行動態選擇,以使量測誤差協方差達到最小。文獻[11]考慮的是雜波存在條件下的目標檢測問題,濾波過程采用概率數據互聯處理雜波,波形捷變方式與文獻[10]相同。文獻[12]是波形捷變傳感器在雜波存在下對多個目標的跟蹤,通過動態選擇4個調制波形來減小量測誤差協方差,并采用聯合概率數據關聯及粒子濾波處理多目標和雜波問題。文獻[13]基本上是對以上工作的整理總結。而文獻[14]對波形的帶寬進行動態選擇,實現距離的量測誤差協方差最小化,并把波形捷變方式應用到MIMO雷達中。盡管上述文獻方法取得了一定的效果,但是其波形捷變方法都只是針對距離維的量測進行的,只考慮了對距離精度的影響,而沒有考慮方位。而目標跟蹤的精度與方位的量測精度有著密切的聯系,尤其當目標相對雷達較遠時,角度誤差對跟蹤精度影響較大。

由上,本文針對二維空間的距離、速度和方位量測采用波形捷變,建立3個變量的誤差的克拉美羅下限方程,通過動態設計或調制雷達發射波形的參量,在一定的范圍內使三者的克拉美羅下限達到最小值,并把此時的克拉美羅下限近似為量測的誤差協方差,提高了信噪比(signal-to-noise ratio,SNR),并提高了距離和方位的跟蹤精度。本文在數據處理上采用粒子濾波來完成目標的跟蹤。另外,與上述文獻方法不同,兩部雷達分別進行波形捷變后再采用多傳感器數據融合,使目標的跟蹤結果更加精確。

1 問題描述

本文采用兩部雷達對空中機動目標進行跟蹤。給出跟蹤過程如圖1所示。

兩部雷達得到量測后采用數據融合方法將結果融合,而融合的系數與二者的量測誤差有關,此時的量測誤差通過波形捷變進行改善,其波形捷變算法流程如圖2所示。

圖1 跟蹤過程流程圖

圖2 波形捷變流程

從圖2可以看出,雷達通過控制發射波形的參量優化了數據處理的效果,而數據處理又反饋指導信息層的參量選擇,即把信息層與數據層相結合來提高最終的跟蹤效果。因此,不但要研究數據層濾波處理時目標的狀態和量測模型,還要考慮雷達發射信號的模型,并建立量測誤差的克拉美羅下限方程將兩者聯系在一起。

2 目標運動模型

2.1 線性狀態模型

目標運動狀態模型由下式給出:

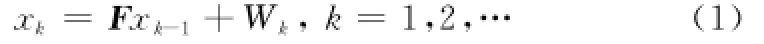
式中,x=(x;x,¨x,y;y,¨y)'是狀態變量,包括目標在笛卡兒坐標中的位置、速度和加速度。過程噪聲W=(wx,wy)'在狀態上產生擾動,為高斯白噪聲,有協方差矩陣Q。轉換矩陣F如下:

式中,T是取樣周期。

2.2 非線性量測模型

考慮目標進行機動,量測變量包括距離、徑向速度和方位角,給出目標的量測方程如下:式中,h(x)是非線性量測,采用目標到雷達的距離、多普勒及方位角作為雷達量測,量測模型與狀態模型存在關系如下:

式中,vk是量測噪聲,也是高斯白噪聲。

3 雷達發射信號模型

噪聲是雷達量測精度的最主要限制。在SNR較大的情況下,并且進一步假設,和某一特定參數有關的量測誤差與任何其他參數中的誤差無關,精度只受接收機噪聲限制,并且所有偏置誤差都已分別考慮。文獻[15]給出了雷達量測M的理論均方根誤差δM的表達式為

式中,k是大約為1的常數;E是接收信號能量;N0是單位帶寬噪聲功率。

因此,雷達的距離、徑向速度及角度的量測誤差與k有關,而k是在固定雷達的相關參量下的值,如果對雷達參量調制就會得到不同的常量k。其中,雷達的徑向速度(頻率)量測精度與信號的有效持續時間有關:

雷達的距離量測精度與時延精度是一致的,而時延誤差可以寫成:

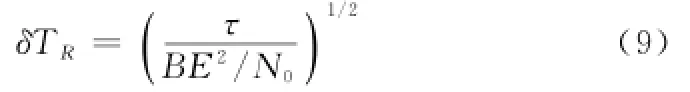
可以簡化為

而角度的量測精度理論表達式來自時延量測精度,因為空域(角度)與頻譜(頻率)域數學上是相似的。因此角度量測的均方根誤差為

式中,γ為有效孔徑寬度,是由孔徑照射(孔徑上的電流分布)決定的。因此,對于不同的照射幅度,角度量測誤差也是不同的,而不同的照射方式,對應的半功率波束寬度也是不同的,因此角度精度可以進一步表示為

根據上面的分析給出具有復雜高斯包絡的信號形式如下:

式中,α為信號的有效持續時間;b為頻率調制率;F(θ)= cos(πθ/2θ0.5),為天線方向圖。由信號形式的設定可以看出不同的參量選擇可以得到不同的信號波形,并通過信號層與數據層的聯系來優化數據層的效果。

4 波形捷變方式

目標在空間機動,采用兩個傳感器進行跟蹤,假設每個傳感器發射的是線性調制波形,主要對其波形參量:脈沖持續時間α、頻率變化率b進行動態選擇。用?=[α b]T表示該傳感器的線性調制波形的參量,建立雷達量測的克拉美羅下限方程,該方程的變量恰好是雷達發射波形的參量,因此量測噪聲的協方差可以用波形的參量表示為N(?)。

4.1 建立量測誤差的CLRB

雷達發射的線性調制波形s(t)如第1節給出,定義其模糊性函數[16]為

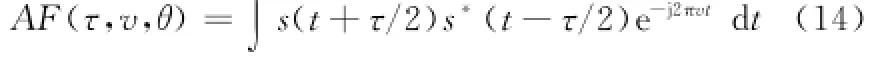
式中,τ和v分別表示波形經目標反射后被雷達接收時的時間延遲和多普勒頻移;θ表示目標偏離法線的角度。這樣,模糊性函數就是關于時延、多普勒和法線偏離角度等信息層變量的函數。建立3個變量的克拉美羅下限方程,因為CRLB[17]是參數估計的理想形式,即Cramer-Rao下界給出了估計的均方誤差下限,實際的估計均方誤差不可能再低于它。這樣,可以得到3個變量估計的最優解。產生Fisher信息矩陣如下:

在理想狀態τ=0,v=0,θ=0時,

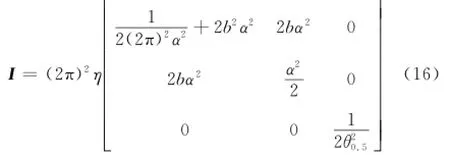
式中,η為雷達的信噪比,則I-1就是參量τ、v和角度θ的估計誤差協方差的CRLB。

根據距離方程及多普勒方程,雷達的量測r和r可以表示為τ和v的形式:r=cv/2;r=cv/(2fc),其中,fc為載頻,而方位角的量測直接對應θ。從而建立了雷達量測誤差協方差與I-1的關系式:

式中,Γ=diag(c/2,c/(2fc),1)。在進行匹配濾波時,選擇使矩陣I-1最小的參量組合,此時的結果就是CRLB方程的最優解,相應得到的量測協方差為一定范圍內的最小值。

4.2 最優參量組合的選擇

由上面的介紹可以看出,通過波形參量的動態選擇來使跟蹤效果達到最佳是波形捷變的最終目的。在這里,采用序貫的方法來進行波形參量的選擇。定義狀態估計的誤差協方差方程如下:

由于不同的波形捷變雷達發射波形的參量是有限的,并且限制在一定的范圍內,因此對參量采用如下的選擇方式:

式中,αmax和αmin分別為信號包絡參量的最大值和最小值; bmax為波形調制的最大可能調制率。從M個α參量和N個b選擇最優配對,使誤差協方差最小。

由以上步驟得到最優的參量組合后,根據第3.2節給出的量測誤差協方差與量測誤差的CRLB的關系,得到優化的量測誤差協方差,并能夠有效提高SNR。把此結果應用于數據處理的濾波過程,實現跟蹤精度的提高。另外,文中采用兩部雷達實施跟蹤,多傳感器的數據融合也是數據處理的一個重要應用。

5 多傳感器數據融合

多個傳感器對目標跟蹤[18],首先帶入坐標及相對位置的問題,如果直接進行各個傳感器之間繁瑣的幾何位置轉換,勢必帶來復雜的誤差轉換,影響跟蹤的精度。

假設兩個雷達對目標進行跟蹤,如圖3所示。兩個傳感器對目標進行觀測,得到觀測值(z1,z2),采用自適應加權算法對數據進行融合,該方法的思想是在總均方誤差最小的最優條件下,根據各個傳感器的量測尋求各個傳感器的最優加權因子。從而使融合后的目標觀測值達到最優。

圖3 雷達與目標位置關系圖

兩雷達數據仍然采用加權方式進行融合,即

則可求得總均方誤差最小時所對應的加權因子為

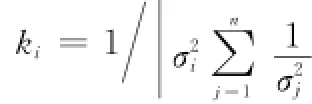
設觀測時存在觀測誤差εi(i=1,2),其均方誤差為σi(i= 1,2),而該誤差及其方差的實時值就是通過上節波形捷變計算得到。波形捷變不僅對量測誤差進行實時更新,而且提高信噪比,從而可以自適應得到多傳感器最優數據融合結果。

6 仿真試驗

6.1 仿真條件

目標在二維空間中機動,采用兩部波形捷變雷達跟蹤,兩部雷達位置設定為[200,975]和[0,220],目標的初始狀態為X0=[1 000,100,1 000,200]T。目標的機動方式設定如表1所示。

__________________表1 目標機動的加速度設定

過程噪聲協方差為

式中,設定T=1。不進行波形捷變的Kalman和粒子濾波的距離量測誤差設定為150 m,角度誤差設定為1°,波形捷變只對距離誤差協方差進行優化的方法(文獻[13])角度誤差也設定為1°。假設雷達發射的為高斯包絡的波形,載波的頻率為fc=5 GHz,有效脈沖寬度為Ts,對所有的波形,當帶寬限定為B=5 k Hz時,脈沖寬度限定在范圍[0.01 s, 0.3 s]內,可進一步限定參量波形包絡持續時間λ,λ=Ts/ε, ε=7.433 8;參量頻率變化率b的范圍限定在[-bmax,bmax],其中最大值bmax=B/(λα)。在距離r處雷達信噪比設定為SNR=(r0/r)4,則目標量測的初始信噪比設為SNR=(r0/ rt)4,r0=10 km。半功率波束寬度設定為θ0.5=3°。在參量選擇過程中,式(19)、式(20)中分別取N=L=10,則參量選擇時的遞歸次數L=(NM)2。

6.2 仿真結果及分析

首先在濾波算法上給出采用波形捷變方式與不采用波形捷變方式的跟蹤效果比較。不采用捷變的方法為Kalman濾波和PF濾波方法,采用捷變的方法為本文方法(同時優化角度和距離)與文獻[13](只對距離誤差進行優化)給出的方法。后兩種方法在數據層也都采用PF進行數據處理,但是通過信息層的波形參量動態選擇來降低量測誤差協方差。

仿真結果如圖4～圖7所示。

圖4 4種濾波方法下的跟蹤結果

圖5 4種濾波方法下距離誤差

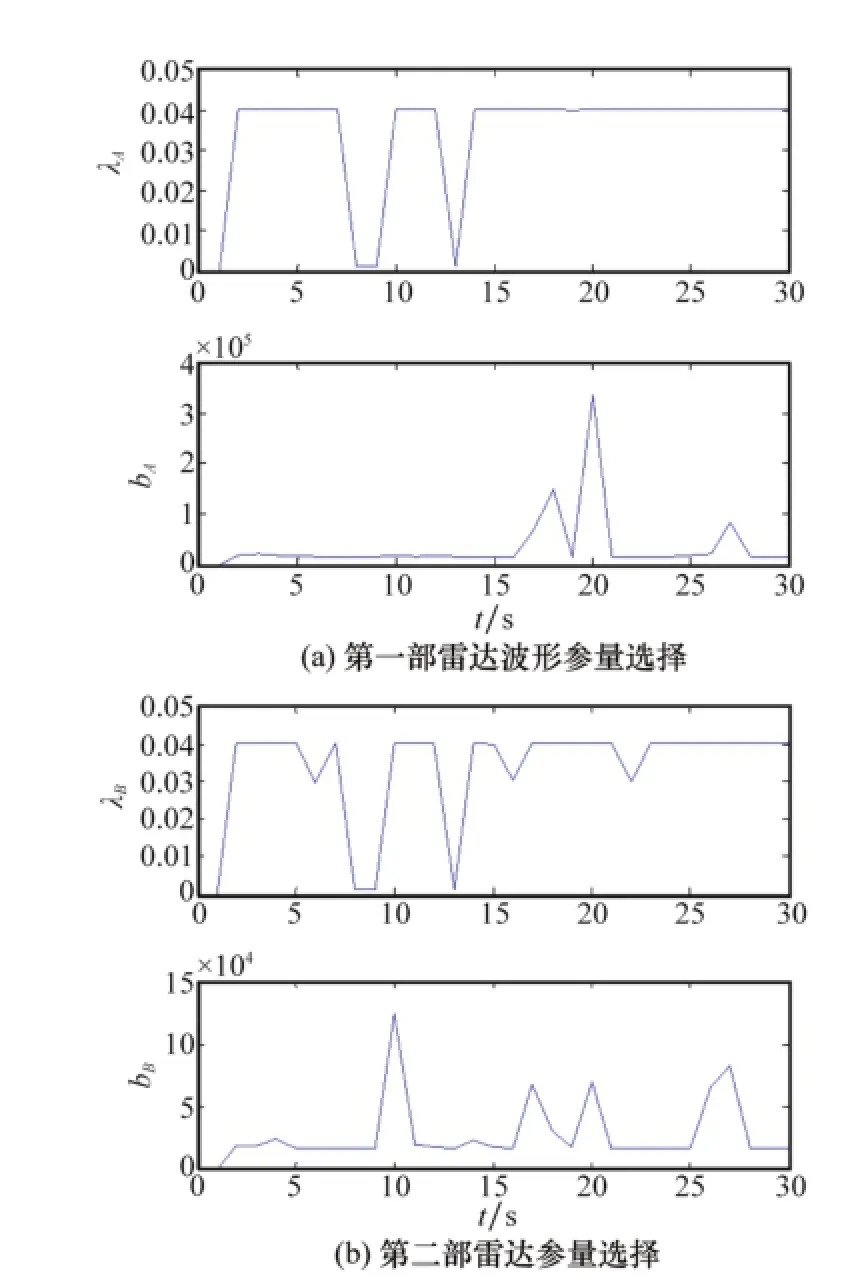
圖6 兩部雷達對脈沖持續時間和頻率變化率的選擇(文獻[13]方法)

圖7 兩部雷達對脈沖持續時間和頻率變化率的選擇(本文方法)

從仿真結果可以看出:

目標采用文中設定的機動方式時,顯然由于Kalman濾波方法只適用于線性運動,因此當目標出現機動時的跟蹤效果較差。而粒子濾波由于其不受系統非線性非高斯的約束,因此在機動部分呈現出較好的效果。目標的跟蹤精度不僅跟數據的處理方式有關,而且與雷達自身的量測精度有著密切的關系。因此,文獻[13]基于一維空間的量測(距離、速度)采用波形捷變的方式來降低雷達的量測誤差協方差。從圖4和圖5可以看出,文獻[13]的跟蹤效果較只采用一種波形的PF方法要好。但是,該文獻只考慮了距離精度的提高,沒有討論角度的精度,而實際上,雷達量測的角度精度對目標的跟蹤精度有著更深的影響。本文基于二維空間的量測(距離、速度和方位角)進行波形捷變,來同時降低距離和角度的量測誤差協方差,提高SNR。在數據處理的過程采用粒子濾波來跟蹤。從圖4和圖5中可以看出,在本文設定的跟蹤環境下,本文的方法具有更好的跟蹤效果,并且跟蹤精度較其他方法有顯著的提高。圖6為采用文獻[13]方法時的參量選擇。圖7為采用本文方法時兩部雷達的參量選擇。

其次,在運動模型處理上IMM是對機動目標跟蹤的一種有效方法。把本文的波形捷變方法與交互多模型進行比較。仿真條件不變,給出仿真結果如圖8～圖11所示。

圖8 跟蹤效果圖

圖9 距離均方誤差

圖8為目標機動時IMM方法和本文方法的跟蹤效果圖,可以看出IMM方法尤其在目標方向變化較大時跟蹤效果不理想。圖9給出了兩種方法相應的跟蹤距離誤差。圖10和圖11為波形捷變時兩部雷達的波形參量的相應取值。上面分別分析了不同濾波方式及不同跟蹤模式下的跟蹤效果,不同濾波方式和跟蹤模式下信噪比的變化及多傳感器融合的效果由表2給出,該結果是在初始信噪比SNR= 6.69 dB,目標真實狀態為[6 196.9 m 160.45 m/s]時各方法下的濾波結果。可以看出無論是采用一部雷達還是兩部雷達跟蹤,基于二維空間波形捷變的跟蹤方法距離精度和速度精度都有較大幅度的提高,而且其信噪比也較實際設定提高。采用一維空間波形捷變方法只是在距離維進行了改進,而其距離精度的提高也證實了方法的有效性。而當跟蹤方式一定時,兩部雷達信息融合的跟蹤效果較單部雷達效果有所改善。

圖10 波形捷變時第一部雷達的參量(脈沖持續時間和頻率變化率)選擇

圖11 波形捷變時第二部雷達的參量(脈沖持續時間和頻率變化率)選擇

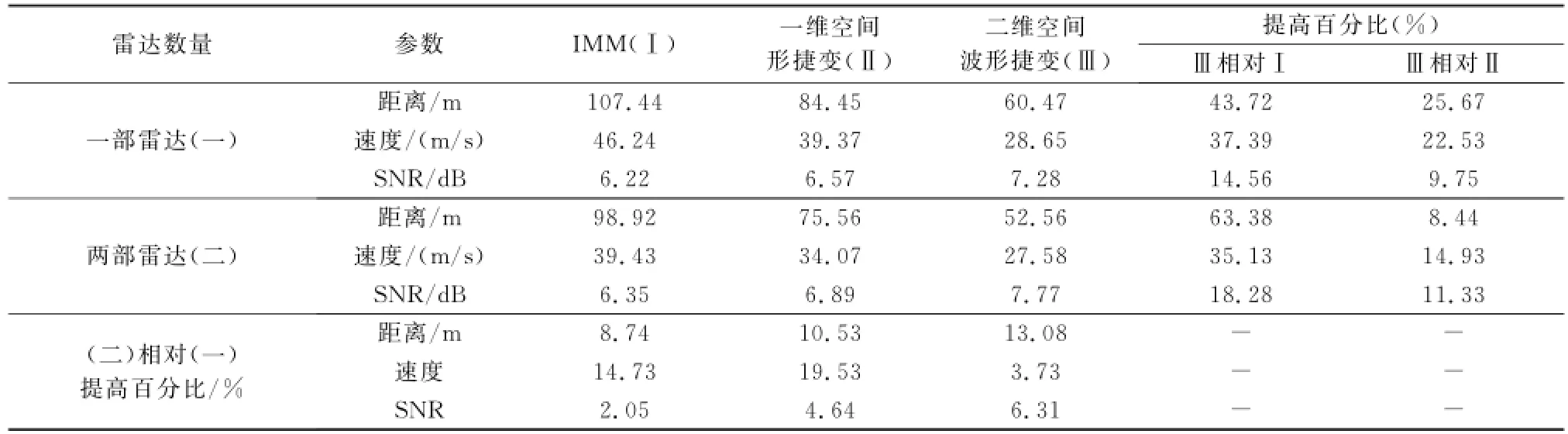
表2 跟蹤模式、濾波方式及雷達數量不同時跟蹤比較

7 結 論

本文研究了機動目標的跟蹤問題,提出了一種基于對二維空間量測進行波形捷變的多傳感器機動目標跟蹤方法。該算法將雷達量測的CRLB近似為量測的誤差協方差,而該CRLB是關于發射波形參量的,因此將目標跟蹤的信號處理和數據處理相結合,通過適時動態選擇雷達發射波形的參量來改變雷達量測的誤差協方差,提高信噪比,提高對距離和方位跟蹤的精度。而跟蹤精度的提高又進一步指導了下一時刻信號處理時的參量選擇。同時,采用多傳感器數據融合及粒子濾波對機動目標進行數據處理,進一步提高跟蹤效果。并在相同的環境下,將本文方法在濾波方式上與Kalman、PF、文獻[13]的方法進行了比較,得到較好的效果;在運動模型方面,與經典的IMM方法進行了比較,也得到了較好的跟蹤效果。

[1]Chang D C,Fang M W.Bearing-only maneuvering mobile tracking with nonlinear filtering algorithms in wireless sensor networks[J].Systems Journal,2014,8(1):160-170.

[2]Han C W,Kang S J,Kim N S.Reverberation and noise robust feature compensation based on IMM[J].IEEE Trans.on Audio, Speech,and Language Processing,2013,21(8):1598-1611.

[3]Song E,Xu J,Zhu Y.Optimal distributed Kalman filtering fusion with singular covariances of filtering errors and measurement noises[J].IEEE Trans.on Automatic Control,2014,59 (5):1271-1282.

[4]Amuso V,Blunt S,Mokole E,et al.Applications and methods of waveform diversity[M].NC:SciTech Publishing,2009.

[5]Stefania B,Andrea C,Andrea G,et al.Sensor radar networks for indoor tracking[J].IEEE Trans.on Wireless Communications Letters,2014,3(2):157-160.

[6]Kershaw D J,Evans R J.Waveform selective probabilistic data association[J].IEEE Trans.on Aerospace and Electronic Systems,1997,33:1180-1188.

[7]Kershaw D J,Evans R J.Optimal waveform selection for tracking systems[J].IEEE Trans.on Information Theory,1994, 40:1536-1550.

[8]Hong S M,Evans R J,Shin H S.Optimization of waveform and detection threshold for target tracking in clutter[C]∥Proc.of the SICE Annual Conference,2001:42-47.

[9]Sira S P,Morrell D,Papandreou-Suppappola A.Waveform design and scheduling for agile sensors for target tracking[C]∥ Proc.of the Asilomar Conference on Signals,Systems and Computers,2004.

[10]Sira S P,Papandreou-Suppappola A,Morrell D.Time-varying waveform selection and configuration for agile sensors for target tracking applications[J].Proc.of the ICASSP,2005.

[11]Sira S P,Cochran D,Papandreou-Suppappola A,et al.Adaptive waveform design for improved detection of low-RCS targets in heavy sea clutter[J].Journal of Selected Topics in Signal Processing,2007,1:56-66.

[12]Sira S P,Papandreou-Suppappola A,Morrell D.Waveform-agile sensing for tracking multiple targets in clutter[C]∥Proc.of the Conference on Information Sciences and Systems,2006: 1418-1423.

[13]Sira S P,Antonia Y L,Papandreou-Suppappola A,et al. Waveform-agile sensing for tracking[J].IEEE Signal Processing Magazine,2009,26(1):53-59.

[14]Zhang J J,Ghassan B M,Papandreou-Suppappola A,et al. Dynamic waveform design for target tracking using MIMO radar[C]∥Proc.of the IEEE Asilomar Conference,2008

[15]Skolnik M I.Introduction to radar systems[M].3rd ed.Zuo Q S, Ma L,Wang D C,et al,trans.Beijing:Publishing House of Electronics Industry,2007:238

247.)

[16]Hu GS.Modernsignal processing tutorial[M].Beijing:Tsinghua University Press,2004:98-103.(胡廣書.現代信號處理教程[M].北京:清華大學出版社,2004:98-103.)

[17]Zhang M Y.Signal detection and estimation[M].3rd ed.Beijing:Publishing House of Electronics Industry,2011:31-32. (張明友.信號檢測與估計[M].3版.北京:電子工業出版社, 2011:31-32.)

[18]Song E,Xu J,Zhu Y.Optimal distributed Kalman filtering fusion with singular covariances of filtering errors and measurement noises[J].IEEE Trans.on Automatic Control,2014,59 (5):1271-1282.

Maneuvering target tracking based on waveform agility with multi-sensor

SHENG Dan,WANG Guo-hong,ZHANG Xiang-yu
(Institute of Information Fusion Technology,Naval Aeronautical and Astronautical University,Yantai 264001,China)

To deal with the case that modern battlefield often has maneuvering targets,a method of maneuvering target tracking is proposed based on waveform-agility with multi-sensors to improve the veracity and accuracy of the performance.First,we establish the Cramer-Rao lower bound(CRLB)function of the measure errors of the sensors.Since the function consists of the parameters of the transmitted waveform,which can be selected adaptively,we can minimize the covariance of the measurements.Then the tracking precision is improved and the signal-to-noise ratio(SNR)is increased.The algorithm given above takes the measurements from two-dimensions space to realize target tracking.And we compare it with the conventional Kalman filtering,particle filtering and the method with waveform-agility which only has measurements from the one-dimension space.Simulation results show that the proposed algorithm provides better tracking performance.

waveform agility;maneuvering;multi-sensor;Cramer-Rao lower bound(CRLB)

TN 958.93

A

10.3969/j.issn.1001-506X.2015.03.02

盛 丹(1983-),女,博士研究生,主要研究方向為信息融合、目標跟蹤。

E-mail:2855221900@qq.com.

王國宏(1963-),男,教授,主要研究方向為數據融合、目標跟蹤。

E-mail:wangguohong@vip.sina.com

張翔宇(1986-),男,博士研究生,主要研究方向為數據融合、目標跟蹤。

E-mail:zxy627289467@sina.com

網址:www.sys-ele.com

1001-506X(2015)03-0485-07

2014 03 13;

2014 06 12;網絡優先出版日期:2014 10 17。

網絡優先出版地址:http:∥w ww.cnki.net/kcms/detail/11.2422.TN.20141017.1611.011.html

國家自然科學基金(60972159,61102165,61179018);“泰山學者”建設工程專項經費資助課題