自錨式懸索橋主纜架設監控

包大海， 袁堂超， 陸久飛

(長安大學公路學院， 西安710064)

?

自錨式懸索橋主纜架設監控

包大海， 袁堂超， 陸久飛

(長安大學公路學院， 西安710064)

自錨式懸索橋在纜索體系施工過程中，主纜線形控制貫穿整個施工過程。主纜架設作為主纜線形控制的首要環節直接影響著主纜線形能否達到設計要求。以浙江中湖大橋主纜架設為例，論述了主纜空纜線形各控制點的確定方法及處理措施；對比標準狀態下解析法與有限元法計算主纜空纜線形結果；研究了無應力索長、跨度、溫度對索股垂度的影響，以便快速、精準地確定基準索股線形。

橋梁工程；自錨式懸索橋；施工控制；主纜架設

引言

自錨式懸索橋是一個自平衡體系，主纜作為主要的傳力部件，主纜線形直接影響著全橋整體受力[1]。主纜線形控制作為自錨式懸索橋施工控制重要組成部分，貫穿整個施工過程。主纜錨固點、散索套IP點和主索鞍IP點作為主纜線形主要控制點，在主纜架設前必須確定其初始狀態。主纜架設作為主纜線形控制第一個環節，其空纜線形直接影響著全橋最終受力能否達到設計要求。對于由預制平行鋼絲索股(PPWS)[2]組成的主纜而言，其空纜線形主要由基準索股線形控制。基準索股線形主要受索股無應力長度、跨度和溫度影響。研究基準索股線形與各影響因素之間關系，對基準索股線形快速調整具有重要的指導意義。

1 工程概況

中湖大橋[3]是一座主跨120 m的三跨混凝土自錨式懸索橋，跨徑組合為45 m+120 m+45 m，橋梁全長214 m，橫斷面寬30 m。主梁為現澆混凝土格子梁體系，主塔為門式鋼筋混凝土框架，全橋共兩根主纜，采用預制平行鋼絲索股(PPWS)，每根主纜由37束平行鋼絲組成，每一束由91根φ5.0 mm的鍍鋅高強絲組成，吊桿縱向間距5 m，橫向間距17 m，全橋吊桿共74根，采用GJ15-22環氧涂層鋼絞線成品索，共869.78 m。大橋整體布置如圖1所示。

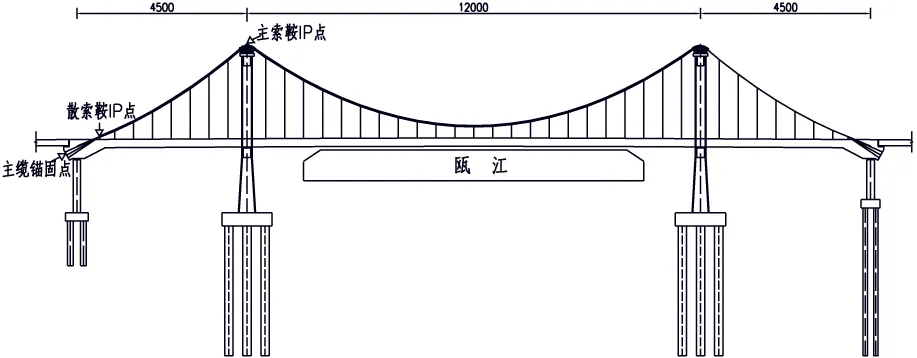
圖1 全橋整體布置圖2空纜線形各控制點的確定及部分處理措施

自錨式懸索橋索股架設是在主塔、主梁施工完成，貓道架設完畢后進行的[4]。主纜錨固點、散索套IP點和主索鞍IP點作為空纜線形的主要控制點，在索股架設前必須確定。由于施工過程中不可避免地會存在誤差，設計中的一些材料特性并不能真實地反應現場實際，伴隨著施工的進行必須對結構狀態進行調整，確保達到設計狀態。

主索鞍IP點：主索鞍設置在主塔上，主塔塔頂偏位及標高直接影響著主索鞍IP點的確定。主塔修筑完成其偏量主要受溫度影響，在索股架設前必須對橋塔進行周日位移持續性觀測。

主梁錨固點、散索套IP點：這兩個控制點設置在主梁上，由多次穩定溫度情況下的測量結果確定。主梁容重、彈性模量在主梁澆筑完成后，根據實際情況進行修正。

主纜參數：主纜各索股在加工完成后，會對部分索股進行張拉試驗，根據實驗結果修正主纜彈性模量等各方面材料參數。

經過現場多次測量及采用數值分析法(懸鏈線理論)[5-7]和有限元分析法計算，得到中湖大橋在穩定溫度、自由狀態下各控制點的偏位及標高見表1。

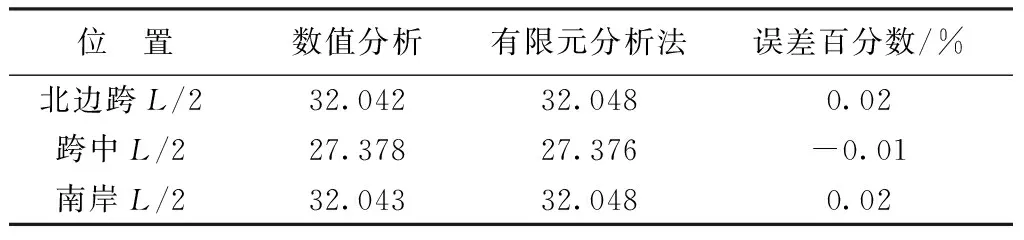
表1 不同計算方法求得空纜各控制點標高(單位：m)

在結構控制點確定以后，必須根據現有實際情況對全橋整體進行受力分析。對個別由于控制點差異較大而引起結構局部受力較大、施工不便的進行適當調整，確保全橋結構在施工中安全、簡便地達到目標狀態。

本橋主塔下部結構屬于高樁承臺，主纜架設初期主塔塔頂偏位受不平衡水平力影響較大。而主索鞍設置預偏的主要目的是為了減少空纜狀態下邊、中跨主纜不平衡水平力對主塔塔頂偏位的影響。預偏量設置最理想狀態是塔頂沒有不平衡水平力出現。由圖2可以看出本工程裸塔具有一定初始偏位，且上下游偏位不一致。為了便于后期結構分析和吊桿對稱張拉，需在設置主索鞍預偏時考慮主塔偏位不同步影響，保證主索鞍IP點上下游絕對里程一致。主塔標高較設計值偏高，可以通過在保證中跨失跨比不變的情況下，適當調整主纜線形。

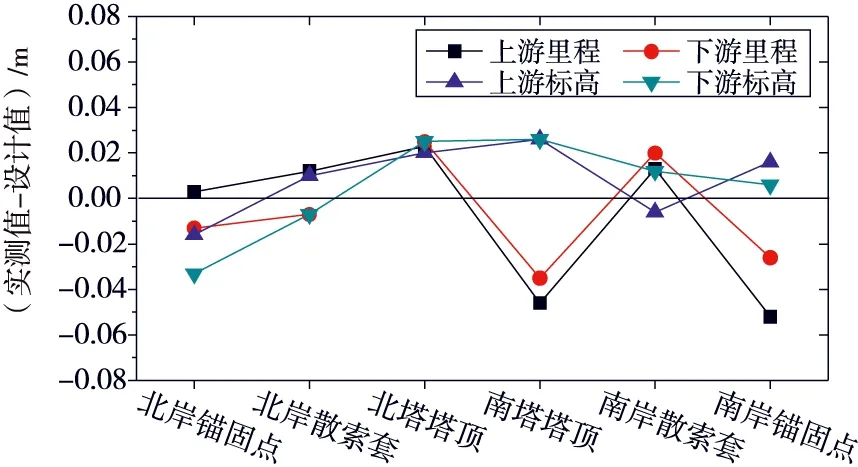
圖2 中湖大橋各控制點偏位

由于工程進度需要主纜在主梁修筑期間開始生產，主纜各索股無應力長度已經確定。由圖2可以看出，主纜錨固點實測值與設計值最大差5.2 cm。雖然主纜在生產時錨頭處有±6 cm的調節量，但是為了減少因主纜錨具錨頭脫空需重新調整索股線形的現象，本工程在南岸上游后錨段增設了3 cm與螺母材質相同的墊塊。

3 空纜線形計算

空纜線形計算是本橋施工控制的關鍵環節。通過大型商業軟件Midas/Civil建立中湖大橋成橋模型。全橋共建立626個單元、623個節點，其中混凝土格子梁采用魚骨式梁單元模擬。主纜與吊桿采用索單元考慮，吊桿下錨點與主梁之間采用剛性連接，由于橋下部結構屬于高樁承臺主塔，必須考慮受不平衡水平力影響較大的樁基偏位。結構空纜狀態模型如圖3所示。根據懸索橋成橋狀態與空纜狀態主纜無應力長度不變的原則[8]，通過倒拆分模型[9-10]求出本工程在主纜建設前的初始狀態、主索鞍和散索套的預偏量。并與現場初始狀態實測值進行對比。對差異較大的控制點通過適當修正主纜無應力長度、主索鞍和散索鞍預偏量，通過正裝模型[9-10]按照實際施工順序達到合理成橋狀態。

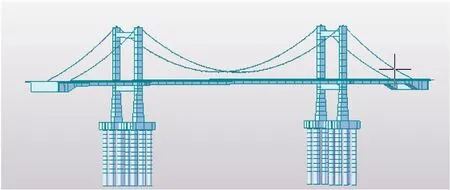
圖3 大橋空纜模型

主纜在空纜狀態下只受自重作用，其空纜線形為懸鏈線。由表1可以看出，采用Midas/Civil有限元軟件計算主纜空纜線形與數值分析法計算結果較為接近，對于中小跨徑自錨式懸索橋而言，數值分析法的計算精度滿足工程要求。

4 索股架設

在主索鞍、散索套預偏量設置完畢后，主纜的空纜線形也隨之確定。由于索股線形受溫度荷載影響較大，基準索股線形精確調整必須在環境溫度穩定的條件下進行。如何快速、精準的使基準索股空纜線形達到設計要求是自錨式懸索橋施工過程中制約工程進度和質量的重要環節。

理論上講，主纜索股在生產過程中會對各跨控制點進行精確標記。但是由于主纜彈性模量、主梁自重、索股架設溫度、各控制點間距及高差都與理論值存在差異，主纜索股架設期間各標記點無法用于精確控制主纜線形。由于索股僅在自重作用下是一條懸鏈線，而懸鏈線的線形主要用垂度表征(垂度指懸鏈線兩端點連線中心到懸鏈線中心的距離)。因此研究索股無應力索長、跨度和溫度對垂度的影響，對后期基準索股線形調整及觀測具有重要指導意義。

4.1 索股無應力索長與垂度之間的關系

在跨度與索股溫度不變的情況下，通過調整各跨索股無應力長度計算出各跨相應垂度。根據模型計算結果以及調索的實測數據發現，主纜垂度和索長之間的關系可近似擬合為線性關系，如圖4所示。

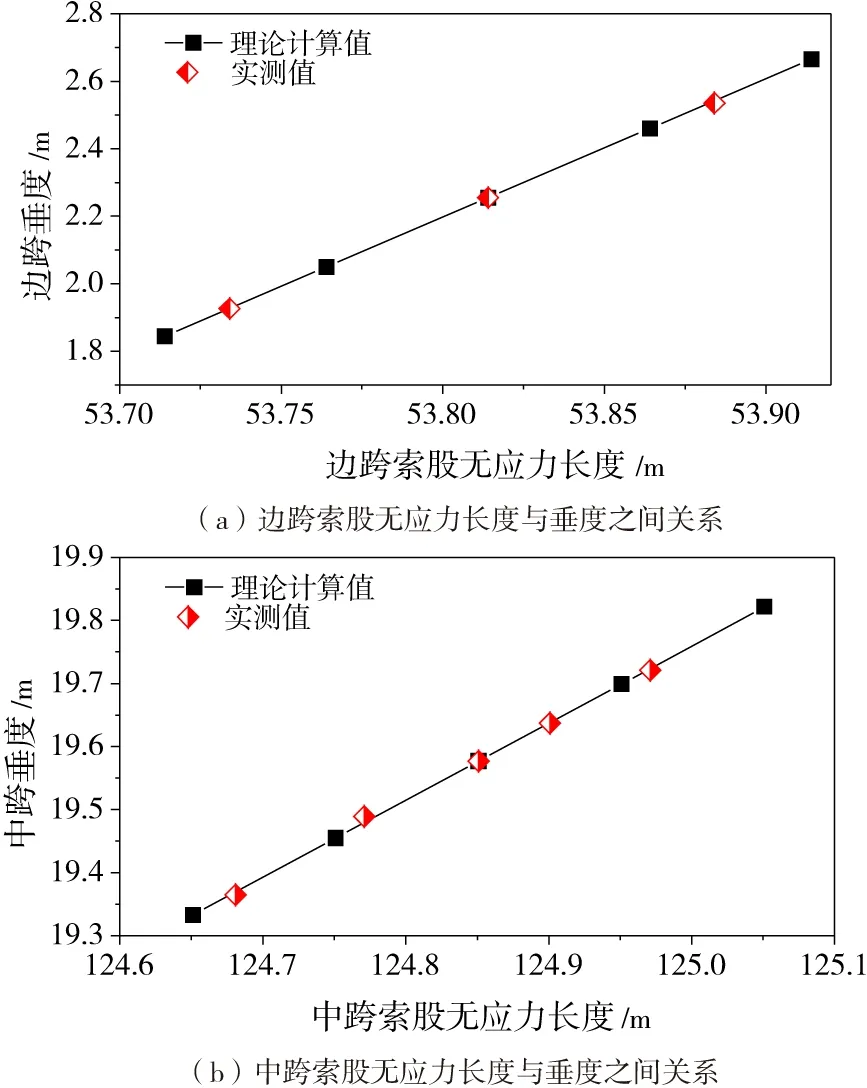
圖4 邊跨、中跨索長與垂度之間的關系

由圖4可以看出在索股線形實際調整過程中，索股索長與垂度之間的線形關系與模型計算結果是相符的。將計算結果與現場實測數據進行擬合可以得到：

邊跨：Δf邊=4.10ΔL邊

中跨：Δf中=1.2225ΔL中

其中，Δf邊、Δf中為邊、中跨垂度改變量，ΔL邊、ΔL中為邊、中跨無應力索長改變量。

4.2 索股跨度與垂度之間的關系

在索股長度與溫度不變的情況下，通過調整索股跨度計算出各跨相應垂度。根據模型計算結果以及實測數據發現，主纜垂度和索長之間的關系可近似擬合為線性關系，如圖5所示。

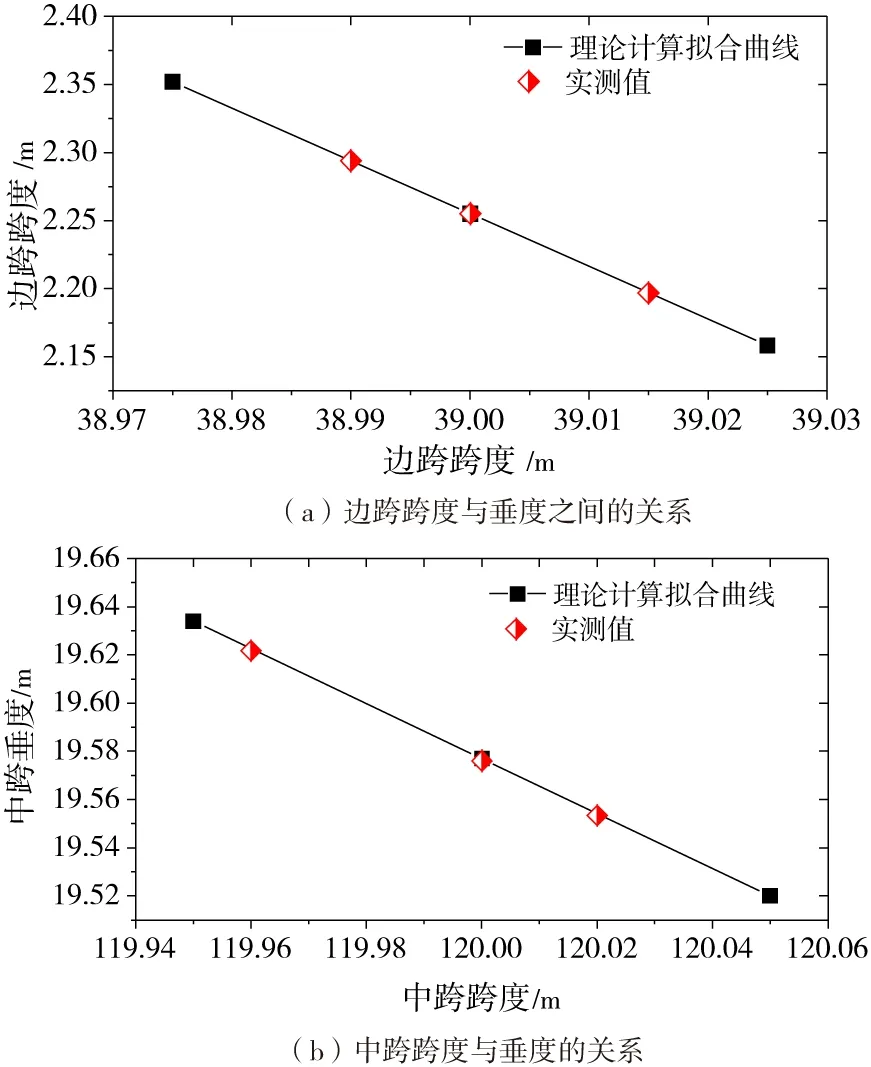
圖5 邊跨、中跨跨度與垂度之間的關系

由圖5可以看出索股跨度與垂度之間符合線形關系，通過模型計算與實測結果相結合擬合出索股跨度與垂度之間的關系：

Δf邊=-3.88ΔL邊

Δf中=-1.14ΔL中

其中，ΔL邊、ΔL中為邊、中跨跨徑改變量。

4.3 索股溫度與垂度之間的關系

主纜在下料時的無應力長度是以20 ℃為基準，但在索股實際架設期間環境溫度是隨著季節與時刻而改變的。為了確保主纜索股線形能夠達到設計狀態，在索股線形調整期間溫度修正是非常重要的。在跨度不變的情況下，溫度變化其實可以簡化為索股索長的改變。因而可以直接推導出溫度與垂度之間的關系。

Δf邊=4.10ΔL邊= 4.10×53.8144×1.2×10-5×Δt= 2.648×10-3×Δt

Δf中=1.2225ΔL中= 1.2225×124.8509×1.2×10-5×Δt= 1.832×10-3×Δt

基準索股線形調整需要在穩定溫度((長度方向Δt≤2 ℃，橫截面Δt≤1 ℃)下進行，一般設在夜間(22∶00～02∶00)。由于天氣、施工等因素影響，現場調索可用時間較短。基準索股線形調整時，首先要根據現場測量結果通過索股跨徑、溫度與垂度之間的關系確定各跨基準索股線形；在索股線形調整過程中根據索長與垂度之間的關系，可以很快使索股線形達到設計要求；在基準索股線形持續性觀測(2～3天)過程中，由于受溫度作用主塔偏位、主纜溫度都會改變，根據換算后的結果判斷索股線形是否穩定。基準索股垂度調整時允許誤差：索股中跨跨中±L/20 000(L為跨徑)=6mm，邊跨跨中為中跨跨中的2倍，上下游基準索股高差為10mm。一般索股參考基準索股±5mm。

5 結束語

本文以中湖大橋為例，詳細介紹了混凝土自錨式懸索橋在索股架設初期主纜線形各控制點的確定方法以及個別影響較大控制點的處理方法；對比有限元法與解析法(懸鏈線理論)計算空纜線形結果，對于中、小跨徑自錨式懸索橋解析法計算結果能夠滿足工程精度的要求；在基準索股架設前能夠將索股無應力長度、跨度和溫度與垂度之間關系確定，對后期基準索線形快速調整及持續性觀測具有重要意義。

[1] 龍飛,許福友,張哲.自錨式懸索橋的特點及工程應用[J].中外公路,2010(5):131-136.

[2] 羅喜恒,肖汝誠,項海帆.懸索橋主纜架設過程分析[J].中外公路,2004(2):8-11.

[3] 韓旭輝,袁陽光,陳安洋,等.自錨式懸索橋主纜下料長度精細化計算[J].重慶交通大學學報:自然科學版,2014(5):13-16.

[4] 孫全勝,高紅帥.自空間主纜自錨式懸索橋體系轉換施工控制[J].重慶交通大學學報:自然科學版,2013(2):112-116.

[5] 張哲.混凝土自錨式懸索橋[M].北京:人民交通出版社,2005.

[6] 嚴偉飛.江山北關大橋的施工監控[D].大連:大連理工大學,2005.

[7] 高榮堂,李傳習,李庭波.平勝大橋自錨式懸索橋基準索股架設的施工控制[J].世界橋梁,2007(1):43-46.

[8] 鐘繼衛,高建學,王戒躁.大跨度懸索橋基準索股施工控制[J].世界橋梁,2006(2):41-43.

[9] 王錦.混凝土自錨式懸索橋施工仿真分析及吊索張拉優化[D].西安:長安大學,2012.

[10] 牛登輝,周志祥,吳海軍,等.自空間自錨式懸索橋體系轉換過程的無應力狀態控制法[J].重慶交通大學學報:自然科學版,2014(1):21-24.

Main Cable Erection Monitoring of Self-anchored Suspension Bridge

BAODahai,YUANTangchao,LUJiufei

(School of Highway, Chang’an University, Xi’an 710064, China)

The main cable shape control is throughout the entire process of cable systems construction of self-anchored suspension bridge. As the primary part of main cable shape control, the erection of main cable has a direct influence on whether the main cable shape can meet the design requirements. This paper discussed the methods and treatment measures to determine the main cable shape of the key points based on the main cable erection of Zhonghu bridge in Zhejiang province. The calculated results of empty cable shape obtained by standard state analytic method and finite element method had been compared with each other. Finally, for the purpose of ascertain the datum strand shape rapidly and accurately, the influence of unstressed cable length, span, temperature on cable strand sag had been discussed.

bridge engineering；self-anchored suspension bridge；construction control；main cable erection

2015-03-21

包大海(1990-)，男，陜西漢中人，碩士生，主要從事橋梁結構分析方面的研究，(E-mail)1207671163@qq.com

1673-1549(2015)03-0076-04

10.11863/j.suse.2015.03.16

U446

A