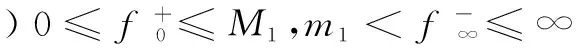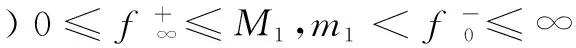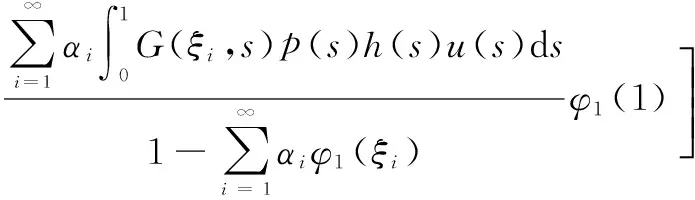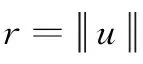Robin型無窮多點邊值問題正解的存在性
覃仕霞, 羅圓
(1.成都信息工程學院應用數學學院, 成都610225;2.西南交通大學土木工程學院, 成都610031)
?
Robin型無窮多點邊值問題正解的存在性
覃仕霞1, 羅圓2
(1.成都信息工程學院應用數學學院, 成都610225;2.西南交通大學土木工程學院, 成都610031)
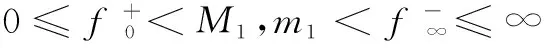
常微分方程;Robin型無窮多點邊值問題;等價積分方程;正解;不動點定理
引言
常微分方程多點邊值問題對應用數學、流體力學及彈性理論等領域的發展都具有非常重要的作用,關于其正解存在性的討論,已成為該領域的一個研究熱點[1-9]。2009年,馬如云[10]等研究無窮多點邊值問題:
并且得到了f在超線性或次線性增長條件下的正解存在性結果。2010年,LuoY[11]等又證明了f在更一般的條件下,上述二階非線性無窮多點邊值問題至少存在一個正解。但關于Robin型無窮多點邊值問題可解性的討論,還未見相關報道。
本文運用錐上不動點定理,討論了Robin型無窮多點邊值問題:
(1)
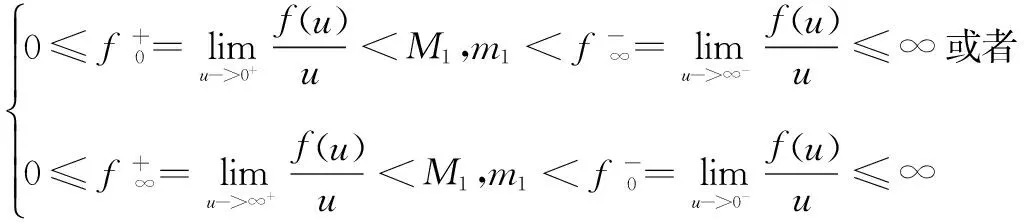
(2)
下正解的情況。通過借助線性方程
u″+a(t)u′+b(t)u=0
(3)
的特解構造新的Green函數,進而證明了問題(1)等價于一個簡單積分方程,然后通過研究此積分方程討論原邊值問題是否存在正解。本文的主要結果改進和推廣了Robin型邊值問題以及無窮多點邊值問題的相關結果。
1 相關引理
本文假設:
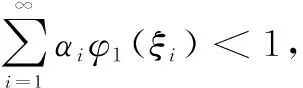
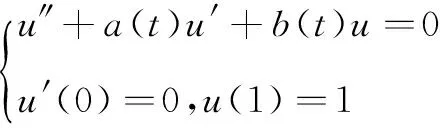
的唯一正解。
(H2)f:[0,∞)->[0,∞)是連續函數,h∈C([0,1],[0,∞))并且存在x0∈(0,1),使得h(x0)>0。
(H3)a∈C[0,1],b∈C([0,1],(-∞,0))。
本文的主要工具是錐上不動點定理。設K是實Banach空間,并且
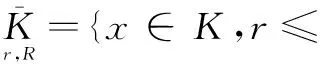
其中,0 引理2[13]假設(H3)成立,設φ1和φ2分別是線性問題 (4) 和 (5) 的解,則 (1)φ1為[0,1]上的不減函數,且φ1>0在[0,1]上。 (2)φ2為[0,1]上的嚴格減函數。 (3)φ2′(0) < 0。 并且問題(4)和(5)均有唯一解。 引理3[14]設x1(t),x2(t),…xn-1(t),xn(t)是方程 引理4設(H1)~(H3)成立,則問題(1)等價于積分方程 (6) 其中 (7) (8) (9) ρ= -φ1(0)φ2′(0) (10) 證明為了方便,令y(t)=h(t)f(u(t))。首先,設u(t)是方程(1)的一個解,驗證它可以由(6)式表示。由引理2可知,線性方程u"+a(t)u′+b(t)u=0有兩個線性無關的解φ1和φ2,因為 所以可以采用常系數變易法,令 再利用引理3得到 (11) 于是將方程(1)的通解表示為: (12) 其中,c1和c2為常數。 再把c1和c2代入(12)式并注意到u(1)=A,ρ=-W(0),化解即可得到 其次,驗證由式(6)定義的u(t)是問題(1)的解。由于 對式兩邊分別對t求導,可推出 把u(t)、u′(t)和u″(t)的表達式以及等式(11)代入u″+a(t)u′+b(t)u中,并利用引理3有 u″+a(t)u′+b(t)u= A(φ″1(t)+a(t)φ1′(t)+b(t)u(t))= A(φ″1(t)+a(t)φ1′(t)+b(t)u(t))= -y(t)+A(φ″1(t)+a(t)φ1′(t)+ b(t)u(t))=y(t) 驗證u(t)滿足問題(1)的邊界條件。由于 那么 綜上所述,(6)式定義的u(t)是問題(1)的解,證畢。 (13) 令 由引理2知,φ1(t)是a≤t≤b上的不減函數,φ2(t)是a≤t≤b上的嚴格減函數,所以有 令M=min{M0,φ1(a)},那么 G(t,s)≥MG(s,s),a≤t≤b,0≤s≤1 (14) 因此,構造由非負函數構成的錐 (15) 定義算子T:C[0,1]→C[0,1]: (16) 由引理4,邊值問題(1)有解當且僅當T在[0,1]上至少有一個不動點。 引理5(ⅰ)TK?K;(ⅱ)T是全連續算子。 證明引理5(ⅰ)由式(13)和引理2可得,G(t,s)≤G(s,s)。因為 所以, 又由式(14)可知 故,Tu∈K并且TK?K。 (ⅱ)不難驗證T:K→K是全連續的,這里不再贅述。 定理1如果(H1)、(H2)和(H3)成立,并且f滿足下面兩個條件之一 其中 則,問題(1)至少有一個正解。 證明由引理4,只需證明T在[0,1]上有一個不動點,再根據引理5,T:K→K是全連續的。證明T滿足引理1的其余部分: (17) 令φ(t)=1,?t∈[0,1],那么φ∈?K1。證明 u≠Tu+λφ,u∈?KR,λ>0 (18) 假設式(18)不成立,那么存在λ0使得u0=Tu0+λ0φ。令δ=min{u0(t):a≤t≤b},由式(17)可知,δ≥η,并且 即δ≥δ+λ0,矛盾。 u≠Tu+λφ,u∈?KR,λ>0 假設該式不成立,那么存在λ0和u0∈?KR使得u0=Tu0+λ0φ。令δ=min{u0(t):a≤t≤b},則可以推出 u0=Tu0+λ0φ= 即δ≥δ+λ0,矛盾。證畢。 [1] Ming H H.Problem of the periodic welding of anisotropic elastic plane with different materials[J].Applied Mathematics and Mechanics,1999,20(7):761-766. [2] Zhan N M,Hong Y M,Dong T L.Application of two-dimensional boundary element method to resonant frequency problem of accelerator cavity[J].Atomic Energy Scinece and Technology,2004,38(1):10-13. [3] Zhang T.A finite element method for pricing American option in bonds[J].Mathematica Numerica Sinica,2004,26(3):277-282. [4] 高潔,周瑋.一類非線性分數階微分方程邊值解的存在性和唯一性[J].應用數學學報,2014,37(3):470-486. [5] 陸心怡,張興秋,王林.一類分數階微分方程m點邊值問題正解的存在性[J].系統科學與數學,2014,34(2):218-230. [6] 林紅緒,楊李凡,胡雨欣.一類帶不連續源項的二階半線性奇攝動Robin型邊值問題[J].應用數學,2015,28(1):47-56. [7] Feng W,Webb J R.Solvability of m-point boundary value problems with non-linear growth[J].J.Math.Anal.Appl,1997,212:467-480. [8] 許丁,謝公南.基于不動點方法求解非線性Falkner-Skan流動方程[J].應用數學和力學,2015,36(1):78-86. [9] Gupta C P,Trofimchuk S I.Sovability of a mult-point boundary value problem and related a priori estimates[J].Canada.Appl.Math.Quart,1998,6(1):45-60. [10] 馬如云,范虹霞,韓曉玲.二階常微分方程無窮多點邊值問題的正解[J].數學物理學報,2009,29A(3):699-706. [11] Luo Y,Wu Z G,Du C.On the positive solutions of some-point boundary value problems[J].Nonlinear Analysis Forum,2010,15:121-128. [12] 郭大均.非線性泛函分析[M].濟南:山東科學技術出版社,1985. [13] 馬如云.一類非線性m-點邊值問題正解的存在性[J].數學學報,2003,46:279-292. [14] 周義倉,勒禎,秦軍林.常微分方程及其應用[M].北京:科學出版社,2003. Beingness of the Positive Solutions for ∞-Point Boundary Value Problems of Robin Type QINShixia1,LUOYuan2 (1.College of Applied Mathematics, Chengdu University of Information Technology, Chengdu 610225, China; 2.School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China) The existence of positive solutions for the second order ∞-point boundary value problems of Robin type was discussed through using the fixed point theorem in cone. Firstly, the special solution of a linear equation was used to construct a new Green function, and then, the differential equation of the ∞-point boundary value problems of Robin type was proved that it is equivalent to a simple integral equation. Finally, the integral equation was studied through using the fixed point theorem and the ∞-point boundary value problems of Robin type mentioned above was derived that there at least exists one positive solution if the condition of 0≤f+0 ordinary differential equation; ∞-point boundary value problems of Robin type; equivalence integral equation; positive solutions; fixed-point theory 2015-05-14 國家自然科學基金項目(11171046) 覃仕霞(1985-),女,湖南常德人,助教,碩士,主要從事應用數學方面的研究,(E-mail)shixiaq@cuit.edu.cn 1673-1549(2015)03-0090-06 10.11863/j.suse.2015.03.19 O29 A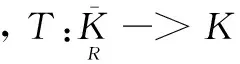
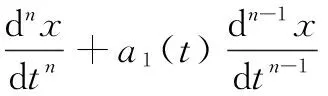
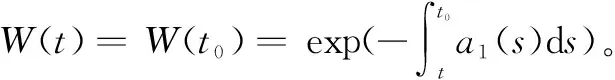

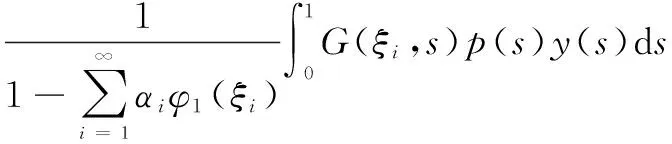
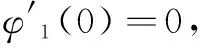
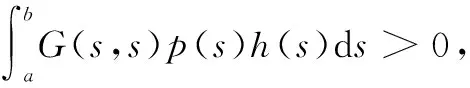
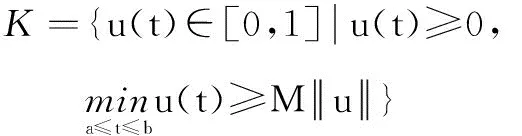
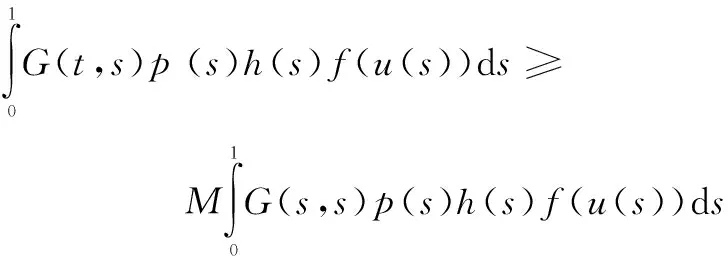
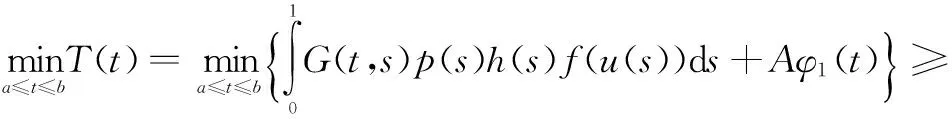
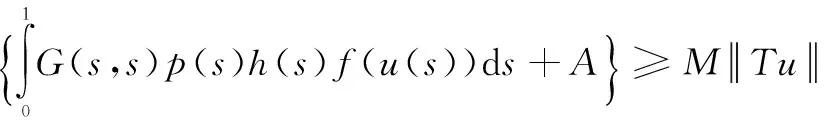
2 主要結果