廣義均值不等式及其簡單應用

王琳， 楊秀

(1.成都理工大學管理科學學院， 成都610059； 2.樂山師范學院數學與信息科學學院， 四川樂山614000)

?

廣義均值不等式及其簡單應用

王琳1， 楊秀2

(1.成都理工大學管理科學學院， 成都610059； 2.樂山師范學院數學與信息科學學院， 四川樂山614000)

將均值不等式從二維空間推廣到n維空間，并著重研究了利用倒推法和反向歸納法證明廣義均值不等式，從而驗證了證明不等式的一般方法的有效性；從形式上和理論上提出廣義均值不等式的冪次一般形式和積分形式，并結合基本均值不等式性質更進一步研究了均值不等式的積分形式的證明，拓展了均值不等式的理論應用范圍。用實例充分體現了均值不等式的性質以及如何結合廣義均值不等式與數學建模思想解決問題，由此說明廣義均值不等式的重要性。

廣義均值不等式；積分形式；二維空間；n維空間；基本均值不等式

引言

均值不等式是證明不等式的重要方法，在教學和研究中也占據著不可替代的位置[1]。運用數學方法解決生活中的現實問題是非常必要的，而運用不等式的原理來分析問題是研究一系列問題的重要方法。在解決數學問題上均值不等式的許多性質起到了非常重要的作用，在現實生活中也有著廣泛的應用[2]。于是，均值不等式的發現、驗證以及應用是當今數學領域研究的主要方向[3-4]。本文著重研究了廣義均值不等式定義證明及其應用，并通過廣義均值不等式的兩種推廣形式的研究突出不等式在數學領域的地位，同時以兩個實例分別研究了廣義均值不等式在理論和實際生活中的應用。

1 廣義均值不等式的定義

調和平均數不超過幾何平均數，幾何平均數不超過算術平均數，算術平均數不超過平方平均數。即：

Hn≤Gn≤An≤Qn

其中，調和平均數Hn：

幾何平均數Gn：

算術平均數An：

平方平均數Qn：

2 廣義均值不等式的證明

基本均值不等式的證明通常用普通證明不等式的方法即可，但廣義均值不等式是在基本均值不等式的基礎上冪的推廣[5]，用簡單的比大小的方式去證明往往說服力不夠[6-8]。廣義均值不等式的證明方法有很多種。例如：數學歸納法(第一數學歸納法或者反向歸納法)、排序不等式法、拉格朗日乘數法和柯西不等式法等。[9-11]

2.1 證明An≤Qn

采用倒推法證明這個不等式，即證：對?xi≥0(i=1,2,…,n)恒有

且其中的等號當且僅當x1=x2=…=xn時成立。

要證明不等式

即證明

展開不等式化簡可得：

2x1x2+2x1x3+…+2xn-1xn

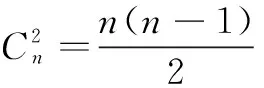
2x1x2+2x1x3+…+2xn-1xn

成立，當且僅當x1=x2=…=xn時等號成立。

所以對?xi≥0(i=1,2,…,n)恒有

其中的等號當且僅當x1=x2=…=xn時成立。

2.2 證明Hn≤Gn≤An

采用反向歸納法，即證：對?xi≥0(i=1,2,…,n)恒有

(1)

且其中的等號當且僅當x1=x2=…=xn時成立。

證明(Ⅰ)先證明命題對一切n=2k(k=1,2,…)成立。

由題知

(2)

當且僅當x1=x2時等號成立。

又因為

利用(2)式可得：

整理得：

當且僅當x1=x2=x3=x4時等號成立。

類似方法，對?k∈N，重復上述方法k次，得：

當且僅當x1=x2=…=x2k時等號成立。

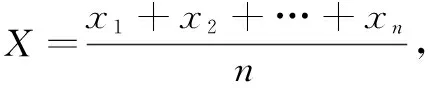
所以有：

Xn+1≥x1x2…xnX

Xn≥x1x2…xn

這表明不等式對n成立。跟n+1時一樣，當且僅當x1=x2=…=xn時等號成立。

由此可知：對?xi≥0(i=1,2,…,n)恒有

且其中的等號當且僅當x1=x2=…=xn時成立。

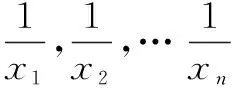
當且僅當x1=x2=…=xn時等號成立。

綜上可知：對?xi≥0(i=1,2,…,n)恒有

且其中的等號當且僅當x1=x2=…=xn時成立。

3 均值不等式的推廣形式

3.1 一般推廣式

設xi≥0(i=1,2,…,n)，記

稱Mr(x)為x1,x2,…,xn的r次冪平均。它與算術平均的關系是：

3.2 平均值不等式的積分形式

設r>0,f(x)>0,p(x)>0，在[a,b] 上有定義，且下面的積分有意義，

記：

則有G(f)≤A(f),G(f)≤Mr(f)，若用

取代p(x)，即有

(r>0,包括r=1的情況)

證明?r>0，

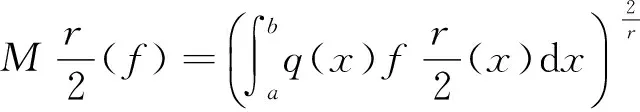
由Schwarz不等式可以得到

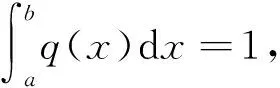
由此有：

(3)

因為f(x)>0,q(x)>0且所在區間[a,b] 上連續，所以在[a,b]上達到最大值，即存在x0∈[a,b]使得

于是有

另一方面因f(x)在x0處連續，?ε>0,?[α,β]?[a,b]使得f(x)>u-ε(當x?[α,β]時)，有

由ε>0的任意性知

且由積分中值定理可知

所以有：

由(1)式證明過程可知

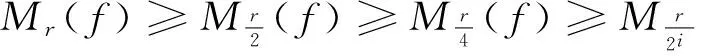
即證

Mr(f)≥G(f)當r=1時，即A(f)≥G(f)。證明過程里“≥”中的等號，當且僅當f(x)≡c時成立，其中c為常數。

4 廣義均值不等式的應用

廣義均值不等式的應用非常廣泛，尤其是在數學領域，在大學數學里廣義均值不等式在求極限、證明積分不等式等方面提供了更簡易更有說服力的方法。

例1設正值函數g(x)在[0,1]上連續，試證：

證明由條件知g(x)，lng(x)在[0,1]上可積。將[0,1]n等分，作積分和，

所以

根據幾何平均數不超過算術平均數可得：

所以有：

例2(均值不等式在數學建模的基本應用)平時在洗衣服時，衣服揉搓充分，再擰一擰把衣服中的水擰掉，但不管怎么擰水也不可能擰干。假設每次洗滌污物都能充分均勻地溶于水中，當水量給定時，如何才能洗得干凈？用水量如何分配？剩余污物量的表達式是什么。

解假設洗滌污物均勻分布在衣服上，并且衣服在開始漂洗前含有一定的水量，其含水量與每次漂洗后衣服的含水量相同，在建模過程中忽略水的溫度，水質等因素對洗滌結果的影響。

y0為衣服上初始污物的含量一定，yi為第i次漂洗衣服用的水量，Y為洗衣服總用水量一定，m為每次漂洗衣服后留下的水的質量一定，n為漂洗衣服的次數，xn為漂洗衣服n次后殘留的污物量。觀察剩余污物xn與每次漂洗衣服的用水量yi的關系，根據題意假設可知第一次放水后，質量為y0的污物均勻分布在質量為m+y1的水中，衣服上剩余的污物量xi與剩余的水量成正比，于是可得：

故有：

重復這樣的步驟，由數學歸納法可得：

(4)

又根據題意可知：

(5)

利用幾何平均數不超過算術平均數則有：

(6)

由(2)式、(3)式和(4)式得：

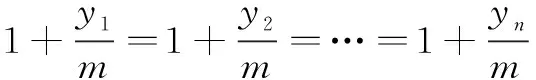
由此可知當漂洗衣服的次數一定時，要使衣服洗得最干凈就應該讓衣服上剩余的污物量xn最小，根據不等式可知當y1=y2=…=yn時，衣服洗得最干凈。此時剩余的污物量為：

5 結束語

本文主要探究廣義均值不等式在理論上和形式上的推廣，通過理論證明將均值不等式的核心思想推廣開，將二維空間里的均值不等式推廣到n維空間，用實例表明均值不等式在解決看似復雜的問題上是有明顯優勢和便利性的。

[1] 沈旭,曾友良.“最近發展區”理論在例題設計中的應用—以“均值不等式求最值”為例[J].當代教育理論與實踐,2013,5(12):14-16.

[2] 劉敏.數學在實際生活中的應用[J].景德鎮高專學報,2014,29(3):28-29.

[3] 陳紀修,於崇華,金路.數學分析(上)[M].北京:高等教育出版社,2004.

[4] 陳紀修,於崇華,金路.數學分析(下)[M].北京:高等教育出版社,2004.

[5] 梁巧麗,李勝平.n元均值不等式的一種新證法[J].思茅師范高等專科學校學報,2005,21(3):50-51.

[6] 秦曉艷.均值不等式的一種簡潔證明[J].佳木斯教育學院學報,2011(2):126.

[7] 李培瑩.走出均值不等式求最值的誤區[J].赤峰學院學報,2014,30(1):4-5.

[8] 黃清明,張江玲,張更容.一類不等式的研究[J].廣西大學學報,2006,31:315-318.

[9] 伏春玲,董建德.均值不等式的性質推廣及應用[J].甘肅聯合大學學報,2010,24(5):26-31.

[10] 王珍娥.均值不等式在一類數列收斂證明中的應用[J].贛南師范學院學報,2007(6):107-109.

[11] 夏立標.均值不等式及其推廣[J].寧德師專學報,2010,22(2):125-127.

Generalized Mean Inequality and Its Simple Application

WANGLin1,YANGXiu2

(1.School of Administrative Science, Chengdu University of Technology, Chengdu 610059, China; 2.School of Mathematics and Information Science, Leshan Normal University, Leshan 614000, China)

The mean inequality is generalized from two-dimensional space to n-dimensional space, and the generalized mean inequality is proved through the reverse derivation method and reverse induction method, which proves the validity of the general approaches of inequality. The power general form and integral form of generalized mean inequality are presented in form and theory, and the method of proving am-gm inequality in integral is further studied through the combination with properties of basic am-gm inequality, then the theory application scope of mean inequality is expanded. Examples fully reflect the natures of am-gm inequality and how to combine it with mathematical modeling thought to solve problems, which shows that the generalized mean inequality is very important.

generalized mean inequality; integral form; two-dimensional space;n-dimensionalspace;basicaverageinequality

2015-04-24

王 琳(1989-)，女，四川仁壽人，碩士生，主要從事運籌學與控制論方面的研究，(E-mail)1101772777@qq.com

1673-1549(2015)03-0096-05

10.11863/j.suse.2015.03.20

O178

A