含隨機填充孔圓形蜂窩結構的面內沖擊性能*

何 強,馬大為,張震東

(南京理工大學機械工程學院,江蘇 南京210094)

含隨機填充孔圓形蜂窩結構的面內沖擊性能*

何 強,馬大為,張震東

(南京理工大學機械工程學院,江蘇 南京210094)

研究多孔材料細觀結構與宏觀力學性能之間的關系,建立具有固定相對密度的含隨機固體填充孔的圓形蜂窩結構模型。在此模型的基礎上具體討論了不同孔洞填充比和沖擊速度對圓形蜂窩結構變形模式、動態沖擊平臺應力以及能量吸收性能的影響。研究結果表明:填充孔在蜂窩變形過程中有局部牽制作用,蜂窩材料變形模式仍為準靜態模式、過渡模式、動態模式;當變形模式為過渡模式或動態模式時,結構的平臺應力與速度的平方成線性關系,存在明顯的速度效應;高速沖擊下,含固體填充孔的蜂窩結構單位質量吸收的能量高于規則蜂窩結構。研究結果可為蜂窩材料的研究和設計提供參考。

固體力學;變形模式;能量吸收;平臺應力;填充孔;圓形蜂窩

蜂窩及多孔泡沫材料作為具有重量輕、比強度和比剛度高 、穩定性好 、隔熱隔聲性好等一系列優點的復合材料,已 經廣泛 應用在 航空、航天 、建筑 、包 裝 等 很 多 領 域[1-2]。 多 孔 材 料 的 力 學 性 能 除 了 與密度和基體材料特性有關外,還與胞元的排列方式、孔壁的缺失等細觀結構密切相關。因此,研究多孔材料細觀結構與宏觀力學性能之間的關系,對于蜂窩及多孔材料的研究和設計都具有很重要的意義。

在蜂窩及多孔材料的實際生產過程中,由于孔壁的坍塌或發泡不完全導致材料中存在實體堆積的現象并不少見,開 孔泡沫 金屬制 備中也 存在顆 粒堆 積 不 理 想 或 未 完 全 消 除 導 致 材 料 密 實 的 情 況[3-4],但是目前關于這方面缺陷對多孔材料力學性能影響的研究還很有限。O.Prakash等[5]對蜂窩材料的實驗研究表明,部分孔的實體填充導致蜂窩局部強化,其彈性模量和應變強化也因此提高,同時結構的密實化應變減小。C.Chen等[6]用有限元方法研究了二維蜂窩結構 準靜態單向和平面 靜 水壓加載下實 體 填充孔對結構彈性模量和屈服應力的影響,發現實體填充孔使蜂窩結構彈性模量略有提高,但對單向屈服強度和平面靜 水屈服 強度影 響不大 。I.Jeon等[3]則通 過實驗 研究發 現因泡 沫垮塌 而出現 實體堆 積的 閉孔泡沫鋁彈性模量低于相同密度的無垮塌缺陷泡沫鋁,材料的塑性垮塌應力則基本不受影響。H.Nakamoto等[7-8]研究了具有線性排列填充孔的六邊形 蜂 窩 結 構 的 面 內 沖 擊 性 能,并 將 其 得 出 的 結 論 與 實驗數據進行了對比。

目前關于含固體填充孔蜂窩結構的研究主要集中在其靜態及準靜態力學性能方面,本文中利用有限元分析軟件 Abaqus對沖擊載荷下具有隨機固體填充孔的圓形蜂窩結構變形過程進行數值模擬,并從蜂窩結構的變形模式、動態沖擊平臺應力及能量吸收能力3個方面研究隨機固體填充孔對蜂窩結構動態力學性能的影響,研究結果可為蜂窩材料的研究和設計提供參考。

1 有限元模型

面內沖擊載荷作用下的規則圓形蜂窩材料計算模型如圖1所示。為了消除尺寸效應,本文所選的規則蜂窩材料結構與 Sun De-qiang等[9]提出的多 層 規 則 排布圓 形 蜂 窩模 型 相 似。 試 件由 具 有 相同 半徑和壁厚的圓形蜂窩胞元方形堆列而成。其中單個胞元的半徑R=3 mm,壁厚t=0.15mm,試件的尺寸為L1×L2=96 mm×96 mm。基體材料為金屬鋁,采用理想彈塑性模型,泊松比ν=0.3,楊氏模量E=69 GPa,密度ρs=2 700 kg/m3,則圓形蜂窩材 料 結 構 的 密 度ρ0=π/2(t/R)ρs=212 kg/m3。采用顯示 動 力 學 軟 件 Abaqus/Explicit對 蜂 窩材料進行動力學特性分析,計算中選用S4R單元(4節點減縮積分殼單元)。為了收斂和計算精度的需要,沿殼厚度方向定義5個高斯積分點。整個壓縮過程中所有可能接觸的表面均定義為自由接觸表面,且無摩擦。采用與文獻[9]相同的邊界條件,即當頂端剛性板沿y方向沖擊蜂窩試件時,底端剛性板固定,結構所有面外位移均被限制以保證其處于平面應變狀態。上下剛性板與蜂窩試件的外表面均視為光滑,兩者接觸無摩擦。模型的面外(沿z方向)厚度b =10 mm。

在規則蜂窩中引入隨機固體填充孔,假定結構的相對密度保持不變,定義孔洞填充比為:

圖1 規則圓形蜂窩材料計算模型Fig.1 Calculation model of regular circular honeycombs

式中:m為蜂窩結構中的隨機固體填充數,N 為蜂窩結構中的胞元總數。容易得到孔洞填充比為α時未填充胞孔的壁厚t滿足下面的方程,即:

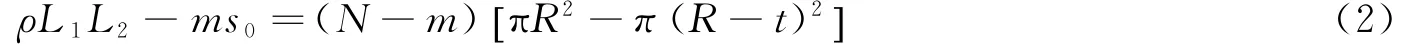
式 中 :s0=πR2為 單 個 胞 孔 的 面 積 ,ρ為 蜂 窩 結 構 相 對 密 度 ,即 :ρ=ρ0/ρs=π/2(t/R)。

為簡化模型,固體填充孔的細觀結構與未填充胞孔相同,將固體填充孔質量均勻分布于胞壁上,可以算得相應的固體填充孔胞元胞壁材料密度為:

式 中 :s=πR2-π(R-t)2,為 胞 壁 的 面 積 。 不 同 孔 洞 填 充 比α的 蜂 窩 結 構 與 未 填 充 胞 孔 壁 厚t及 胞 壁 材料密度ρe的對應關系如表1所示。

本文中所研究的二維蜂窩結構的相對密度為0.1,其剛度和強度遠低于固體填充孔。因此,固體填充孔可通過改變胞壁材料楊氏模量和屈服強度為規則蜂窩結構胞壁材料相應值的1 000倍引入,與 C.Chen等[6]的有限元模 型 相同。本文中對同一孔洞填充比計算了3組不同隨機樣本的含隨機固體填充孔圓形蜂窩結構。

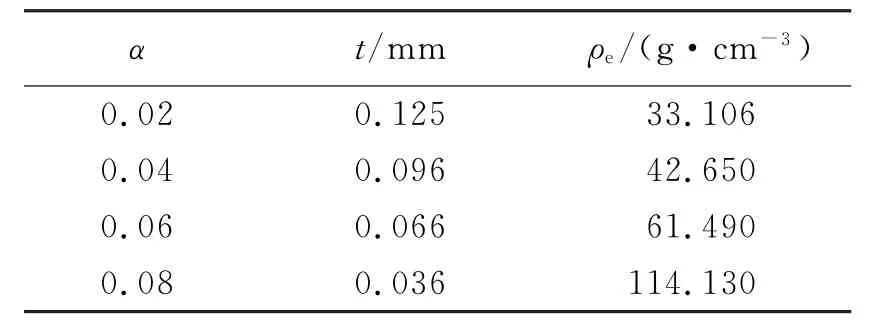
表1 含隨機固體填充孔蜂窩結構參數Table 1 Parameters of honeycombs with randomly arranged solid inclusions

2 計算結果與分析

2.1 變形模式

限于篇幅,圖2僅給出了α=0,0.04時,不同沖擊速度下圓形蜂窩結構的變形模式圖。當沖擊速度為3 m/s時,蜂窩結構沖擊端和固定端的應力基本相同,變形模式均為準靜態模式,在初始壓縮變形階段,整個蜂窩試件的變形是均勻的,各個胞元均具有橫向擴張。緊接著,變形不再是均勻的,部分胞元開始交替平行地發生坍塌,很多胞元被4個橢圓坍塌胞元圍住,結構總體變形呈現“分布崩塌帶”模式,結構中的填充孔對崩塌帶的分布有微弱影響,所有固體填充孔必然會被坍塌的橢圓形胞元包圍。隨著相對壓縮量的增大,胞元逐層壓縮直至蜂窩材料密實化。

圖2 圓形蜂窩材料變形輪廓圖Fig.2 Deformation profile of circular honeycomb

隨 著 沖 擊 速度的提高 (v=40 m/s),規則蜂窩結構變形由準靜態模式轉變為過渡模式。變形初始階段,慣性效應使得蜂窩結構在靠近沖擊端處出現變形局部化,結構沖擊端應力處于應力應變曲線的壓實應變側,因此高于準靜態模式下的壓縮應力值。隨著相對壓縮量的增大,規則圓形蜂窩結構中部的胞元變形要早于蜂窩結構兩邊的胞元,使得蜂窩結構整體變形出現“V”形變形帶,而固體填充孔在變形過程中具有一定的牽制效應[5],使含填充孔蜂窩結構靠近沖擊端的變形局部化現象更加明顯,且變形帶向結構兩側擴展,呈現出倒置“W”形。

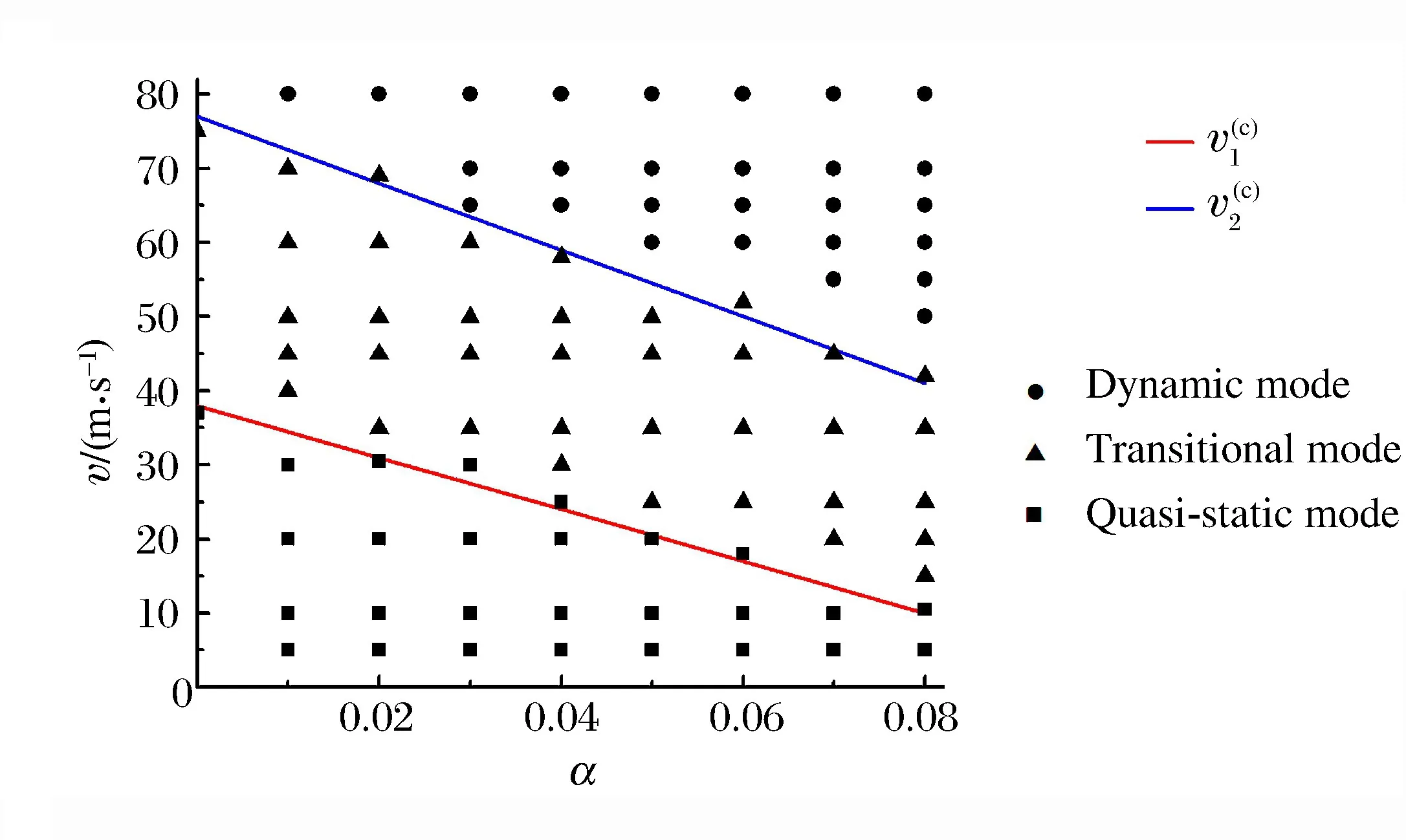
圖3 圓形蜂窩結構的變形模式Fig.3 Deformation mode of the circular honeycomb

沖擊速度進一步增加為100 m/s時,含填充孔的圓形蜂窩結構 的變形過程與規則蜂窩材料的 變 形模式類似,只產生一個呈“I”形狀的局部變形帶,對應著從沖擊端到固定端的逐層壓潰變形模式。與含隨 機 固 體 填 充 孔 六 邊 形 蜂 窩 結 構 的 動 態 壓 縮 變 形 模 式 不 同[7],圓 形 蜂 窩 結 構 密 實 化 時,所 有 的 胞 元(除填充孔外)均被壓實,并沒有出現滲漏效應(當蜂窩結構壓縮至密實化應變時,部分被固體填充孔包圍的未完全坍塌的胞元將不再發生變形)。

研究不同填充比的蜂窩結構在不同沖擊速度下的變形模式,結果表明隨機填充孔圓形蜂窩材料的變形模式包括準靜態模式、過渡模式及動態模式,即固體填充孔并沒有改變圓形蜂窩結構y方向動態沖擊時的變形模式。圖2則給出了這幾種典型變形模式的變形輪廓圖。

圖3則給出了不同填充比下蜂窩結構變形模式轉變時的沖擊速度值。填充孔的引入對臨界速度有一定的影響,根據圖3中的數據,得到含填充孔蜂窩結構由準靜態變形模式向過渡模式轉變的臨界速度v1(c)和 由 過 渡 模 式 向 動 態 模 式 轉 變 的 臨 界 速 度v2(c)的 近 似 公 式:

2.2 沖擊端平臺應力的速度效應

作為表征多胞材料能量吸收能力大小的重要參數,平臺應力σp定義為沖擊端剛性板壓縮應力從第1個 應力峰 值到試 件密實 化前最 大應變 所對應 的壓縮 反力的 平均名 義應力[10],即定 義平臺 應力為 :

式中:名義應力σ為剛性板作用在試件上的壓縮反力F與初始橫截面積A(L2×b)的比值,名義應變ε定 義 為 試 件 在y 方 向 的 壓 縮 量 與 初 始 長 度L1之 比 ,εd為 蜂 窩 結 構 的 密 實 化 應 變 值 ,εy為 屈 服 應 變 ,本 文中取εy=0.02[9]。

分析可得,當沖擊速度大于由準靜 態 變 形 模 式向 過 渡 模 式 轉 變的 臨 界 速 度v(c)1時,平 臺 應 力σp與v2呈線性關系,并且可以由以下公式擬合:

式中:a1和a2為擬合系數。

圖4(a)給出了含填充孔的圓形蜂窩結構沖擊端平臺應力與速度參量v2之間的關系,圖4(b)所示為局部放大圖。從局部放大圖中也能夠看出,當沖擊速度小于臨界速度v(c)1,即蜂窩結構的變形仍處于準靜態模式時,沖擊 端平臺 應力曲 線 表 現 出 明 顯 的 非 線 性。S.R.Reid等[11]基 于 一 維 沖 擊 波 理 論 建 立 了均 勻多孔材料動態沖擊平臺應力σp與沖擊速度之間的關系,并指出當沖擊速度大于一定值時,規則蜂窩結構的平臺應力存在速度效應,平臺應力值與速度的平方成線性關系。各蜂窩結構的擬合參數值如表2所示,本文中的擬合結果表明,當蜂窩結構中含有隨機固體填充孔時這樣的速度效應同樣存在,但此時擬合參數與填充比的大小有關。從表中可知,隨著填充比的增大,擬合參數a2也有所增大,這說明填充比的增加使得圓形蜂窩結構沖擊端平臺應力的速度效應更加明顯。

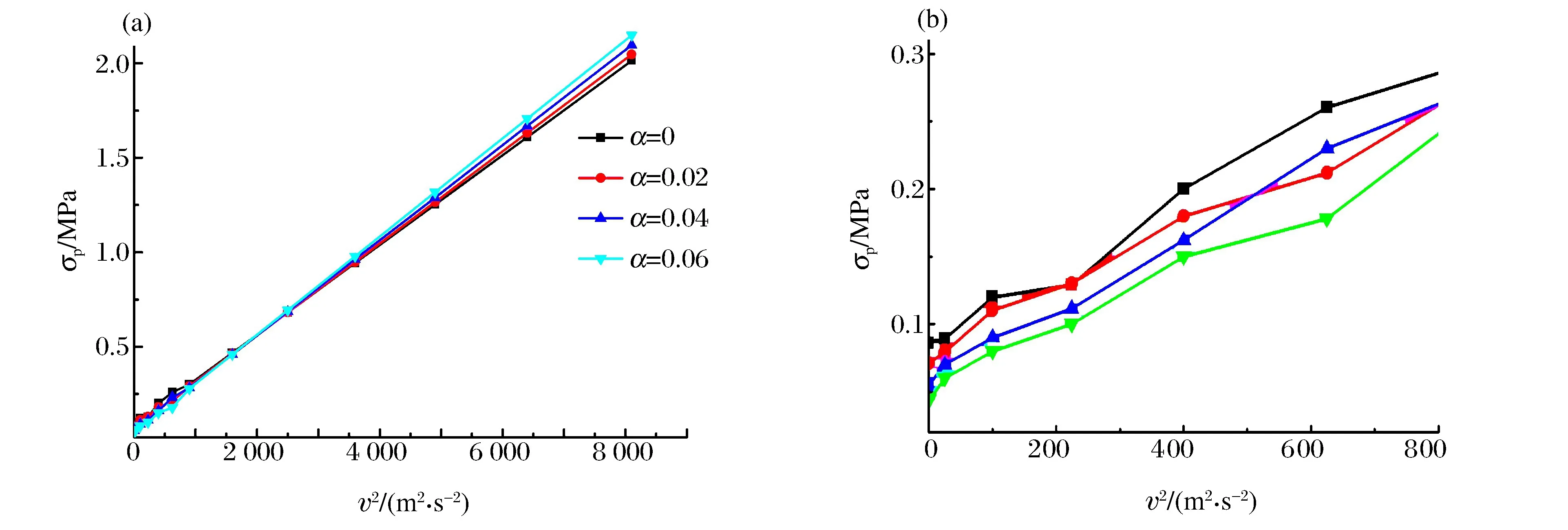
圖4 沖擊速度對平臺應力的影響Fig.4 Effect of impact velocity on the plateau stress of honeycombs

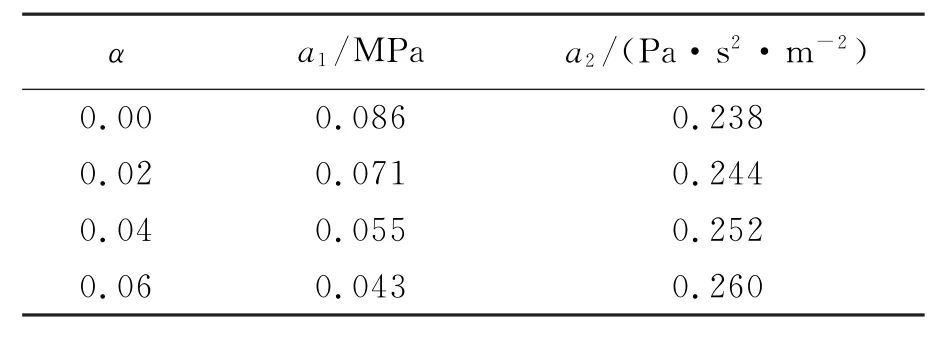
表2 平臺應力擬合關系式中的系數Table 2 Coefficients in fitting equation of plateau stress

2.3 固體填充孔對沖擊端平臺應力的影響

圖5給 出 了 低 速 沖 擊 時(v=3 m/s)4 種 蜂 窩 結 構 沖 擊 端 的 名 義 應 力 應 變 曲 線 。研 究 的 蜂 窩 結 構 模型相對密度保持不變,隨著孔洞填充比的增大,變形胞元孔的壁厚明顯變薄,圓形蜂窩結構沖擊端的應力平臺降低。此時蜂窩結構均處于準靜態變形模式,規則蜂窩沖擊端壓縮應力曲線較為平緩,含固體填充孔的圓形蜂窩結構因為填充孔附近的崩塌變形以及變形局部化區域的宏觀密度突然提高,使得蜂窩結構的應力明顯變大,沖擊端應力應變曲線出現了應力尖峰值,當固體填充孔與沖擊面的速度一致時,應力幅值回落。另外,隨著孔洞填充比的增大,蜂窩結構的密實化應變值變小,由于未出現滲漏現象,其密實化應變值減小的幅度小于含隨機固體填充孔的六邊形蜂窩結構[7]。

定義相對平臺應力為含固體填充孔圓形蜂窩結構沖擊端平臺應力σp*與規則圓形蜂窩結構沖擊端平臺 應 力σp(0)之比。圖6所示為蜂窩結構在y方向上受沖擊時沖擊端相對平臺應力隨沖擊速度的變化關系。低速沖擊下,隨著孔洞填充比的增大,變形胞孔壁厚的減小使得蜂窩結構沖擊端的承載能力顯著下 降,如 圖 中 所 示 ,沖 擊 速 度 為3 m/s時 ,α=0.06 的 蜂 窩 結 構 平 臺 應 力 約 為 相 同 相 對 密 度 的 規 則 蜂 窩結構平臺應力的50%。

隨著沖擊速度的增大,蜂窩結構變形向沖擊端附近移動,慣性效應引起的變形局部化使得結構平臺應 力 增 加 。 對 于α=0.04,0.06的 蜂 窩 結 構,填 充 比 的 增 大 使 得 胞 元 壁 厚 變 薄,一 定 程 度 上 會 導 致 結 構壓縮應力的下降,但是固體填充孔的牽制效應使得動態沖擊的慣性效應影響增強,導致蜂窩結構沖擊端應力應變曲線中出現應力尖峰,提高了蜂窩結構的吸能能力,這一增強效應很明顯,因而在沖擊速度小于40 m/s時,隨 著 沖 擊 速 度 的 提 高,相 對 平 臺 應 力 會 顯 著 增 強 。 當 沖 擊 速 度 達 到40 m/s時,含 固 體 填充孔蜂窩結構的平臺應力與規則蜂窩結構平臺應力基本相同。繼續加大蜂窩結構的沖擊加載速度(v> 80 m/s),慣性效應的影響起主要作用,胞元的主要變形由低速時的交替平行胞元坍塌變為由接觸 點 處開始向內凹陷崩塌的逐層壓縮變形,且蜂窩結構的變形開始慢慢地集中在沖擊端附近,這就使得規則蜂窩結構的平臺應力也明顯增強,從而削弱了相對平臺應力的增 長,當速度達到100 m/s時候,相對 平 臺應力甚至有下降的趨勢。

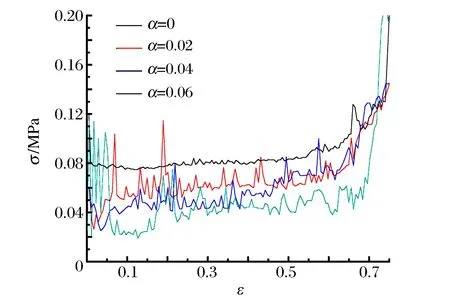
圖5 低速沖擊下圓形蜂窩上材料沖擊端動態響應曲線Fig.5 Dynamic response curve of circular honeycomb at the crushing end

圖6 固體填充孔對y方向相對平臺應力的影響Fig.6 Effect of solid inclusions on the relative plateau stress in y direction

2.4 隨機填充孔對能量吸收特性的影響

作為一種高效的阻尼材料,多孔胞元材料已被廣泛地應用于各種能量吸收結構中。評價多胞材料與結構能量吸收能力大小的重要指標就是單位質量吸收的能量大小[12]:

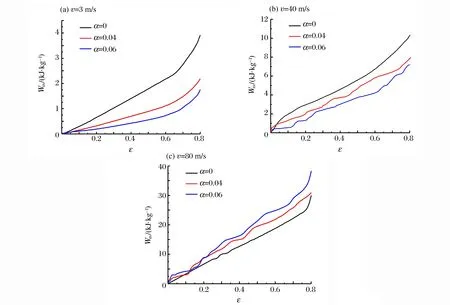
圖7 不同沖擊速度下蜂窩結構單位質量吸收能量Fig.7 Energy absorption of honeycombs structures at different impact velocities

由圖7可見,低速沖擊下(v=3 m/s)因為各蜂窩結構均處于準靜態壓縮模式,單位質量能量吸收曲線較為平滑,固體填充孔并沒有提高蜂窩結構的能量吸收能力,相反,胞元孔壁厚度的減小降低了沖擊端的應力值,導 致含填 充孔蜂窩 結 構 的 吸 能 能 力 下 降,當ε=0.8 時,α=0.06 的 蜂 窩 結構單位 質 量 吸收能量大小僅為規則圓形蜂窩結構的37.5%。當沖擊速度為40 m/s時,蜂窩結構的單位質量吸收能量與低速沖擊時相比均有所提高,固體填充孔的存在提高了蜂窩結構的吸能能力,減小了與規則蜂窩結構單位質量吸收能量大小之間的差距,當ε=0.8 時,α=0.06 的 蜂 窩 結 構 單 位 質 量 吸 收 能 量 大 小 為 規 則圓形蜂窩結構的72%。當沖擊速度為80 m/s時,蜂窩結構都處于動態沖擊模式,慣性效應起到了主要的作用,固體填充孔的牽制效應使得蜂窩結構的變形局部化更加明顯,盡管含隨機固體填充孔的蜂窩結構胞壁較薄,但是其沖擊端應力值仍大于規則圓形蜂窩結構,單位質量吸能能力大大提升。由圖7(b) ~(c)也能看出,含隨機固體填充孔蜂窩結構沖擊端應力應變曲線中出現的應力峰值使得單位質量吸收能量曲線體現了局部的凹凸性。

3 結 論

本文中討論了隨機固體填充孔對圓形蜂窩結構材料的面內沖擊性能的影響。計算結果表明:

(1)含固體填充孔的圓形蜂窩結構與相同相對密度的規則圓形蜂窩結構具有相同的變形模式,即準靜態模式、過渡模式及動態模式,但填充比對變形模式的臨界速度有影響。

(2)當含隨機固體填充孔的圓形蜂窩結構變形處于準靜態模式時,沖擊端平臺應力曲線表現出明顯的非線性,沖擊速度大于由準靜態變形 模 式 向過渡模式轉 變 的 臨 界速度v(c)1時,平臺 應 力σp與v2呈 線性關系,存在明顯的速度效應。

(3)低速沖擊下,含固體填充孔的蜂窩結構平臺應力隨孔洞填充比的增大而顯著降低,導致含填充孔蜂窩結構的吸能能力下降,沖 擊速度 為3 m/s時,α=0.06 的蜂窩 結構平 臺 應 力 約 為 相 同 相 對 密 度 的規則蜂窩結構平臺應力的50%,單位質量吸收能量大小僅為規則圓形蜂窩結構的37.5%。隨著沖擊速度的提高,固體填充孔的牽制效應使得動態沖擊的慣性效應影響增強,沖擊端應力應變曲線出現明顯的應力尖峰,提高了蜂窩結構的單位質量吸能能力。

本文中對含隨機固體填充孔的圓形蜂窩結構的面內沖擊性能的研究可為有缺陷蜂窩材料的研究提供參考,但關于隨機固體填充孔與蜂窩結構動態響應特性更深層次的探討還有待進一步展開。

[1]Gibson L J,Ashby M F.Cellular solids:structure and properties[M].2nd ed,Cambridge:Cambridge University Press,1997:93-147.

[2]盧 天 健,何 德 坪,陳 常 青,等.超 輕 多 孔 金 屬 材 料 的 多 功 能 特 性 及 應 用[J].力 學 進 展 ,2006,36(4):517-535. Lu Tian-jian,He De-ping,Chen Chang-qing,et al.The multi-functionality of ultra-light porous metals and their applications[J].Advances in Mechanics,2006,36(4):517-535.

[3]Jeon I,Asahina T.The effect of structural defects on the compressive behavior of closed-cell A1 foam[J].Acta Materialia,2005,53:3415-3423.

[4]Kepets M,Lu T J,Dowling A P.Modeling of the role of defects in sintered FeCr Al Y foams[J].Acta Mechanica Sinica,2007,23(5):511-529.

[5]Prakash O,Bichebois P,Brechet Y,et al.A note on the deformation behaviour of two-dimensional model cellular structures[J].Philosophical Magazine A:Physics of Condensed Matter Structure Defects and Mechanical Properties,1996,73:739-751.

[6]Chen C,Lu T J,Fleck N A.Effect of inclusions and holes on the stiffness and strength of honeycombs[J].International Journal of Mechanical Sciences,2001,43(2):487-504.

[7]Nakamoto H,Adachi T,Araki W.In-plane impact behavior of honeycomb structures randomly filled with rigid inclusions[J].International Journal of Impact Engineering,2009,36(1):73-80.

[8]Nakamoto H,Adachi T,Araki W.In-plane impact behavior of honeycomb structures filled with linearly arranged inclusions[J].International Journal of Impact Engineering,2009,36(8):1019-1026.

[9]Sun De-qiang,Zhang Wei-hong.In-plane crushing and energy absorption performance of multi-layer regularly arranged circular honeycombs[J].Composite Structures,2013,96:726-735.

[10]Tan P J,Reid S R,Harrigan J J,et al.Dynamic compressive strength properties of aluminum foams:PartⅠ: Experimental data and observations[J].Journal of the Mechanics and Physics of Solids,2005,53(10):2174-2205.

[11]Reid S R,Peng C.Dynamic uniaxial crushing of wood[J].International Journal of Impact Engineering,1997,19 (5/6):531-570.

[12]Kooistra G W,Deshpande V S,Wadley H N G.Compressive behavior of age hardenable tetrahedral lattice truss structures made from aluminum[J].Acta Materialia,2004,52(14):4229-4237.

In-plane impact behavior of circular honeycomb structures randomly filled with rigid inclusions

He Qiang,Ma Da-wei,Zhang Zhen-dong
(School of Mechanical Engineering,Nanjing University of Science and Technology, Nanjing 210094,Jiangsu,China)

The model of circular honeycomb structures randomly filled with rigid inclusions which keeps the relative density as a constant is developed.And then the effects of impact velocity and packing ratio on the deformation modes,dynamic plateau stress and energy absorption capacities are discussed in detail.Research results show that the rigid inclusions have pinning effect in the process of deformation and the deformation modes can still be classified as quasi-static mode,transitional mode and dynamic mode.The plateau stress is proportional to the square of the impact velocity when the honeycombs are deformed at transitional mode or dynamic mode,which shows obvious speed effect. The energy absorption capacities of circular honeycombs are higher than these of the regular honeycombs at high-velocity impact.These results can provide valuable suggestions in the study and design of the functionally gradient honeycombs.

solid mechanics;deformation modes;energy absorption;plateau stress;inclusions;circular honeycomb

O347國標學科代碼:13015

:A

10.11883/1001-1455-(2015)03-0401-08

(責任編輯 王易難)

2013-09-17;

2014-02-21

何 強(1989— ),男,博士研 究生,18260098162@163.com。