基于路面不平整度的車輛動荷載系數分析

楊春風，解 帥，孫吉書

(河北工業大學 土木工程學院，天津 300401)

?

基于路面不平整度的車輛動荷載系數分析

楊春風，解 帥，孫吉書

(河北工業大學 土木工程學院，天津 300401)

為更好地研究路面不平整度下車輛對路面的動載作用，運用1/4車輛振動模型，借助MATLAB數學計算軟件，分析路面不平整度、車輛參數等因素對動載系數的影響規律。結果表明：車速、路面振幅對動載系數影響很大，路面振幅與動載系數呈線性關系，驗證了路面不平整是導致動載的主要原因；汽車結構參數中的輪胎阻尼、懸架剛度、懸架阻尼對動載系數影響較小，但減小輪胎剛度可以顯著地減小動載。從道路設計的角度考慮，提高道路的平整度是減小動載的重要措施。

道路工程；振動模型；車輛參數；動載系數

0 引 言

車輛在路面上行駛，是一個車路相互作用的過程。由于道路的不平整和車輛自身的振動，造成車輛對路面產生不可避免的動載作用，這個作用遠大于道路設計規范中的靜載，它在破壞道路的同時也會影響駕駛的安全性和舒適度，最終形成惡性循環，大大降低了道路使用壽命。

目前，國內外一些專家學者開始研究車輛荷載對路面結構的動態作用。D. Cebon[1]研究了車輛結構對胎壓和路面的動態影響，并做了一些優化設計；R.V.Siddharthan等[2]利用傅立葉變換的有限元計算方法，基于輪胎和路面的接觸，模擬了實際移動荷載對路面的力學作用；日本的寺擇寬一運用貝塞爾函數，在彈性半空間體的軸對稱作用下，推導了計算路面位移和應力的函數計算式。國內最早開始研究路面動力學的是鄧學鈞和孫璐[3]，他們利用車輛對地面結構隨機的振動，研究了各種運動荷載下的路面結構力學響應；葉開沅等[4]考慮在動載質量、慣性力及阻尼作用下，研究了車輛通過連續梁時的振動過程，并得出了任意運動荷載作用下連續梁的動力解析解；為減小動荷載，余卓平等[5]對車輛的優化設計了汽車懸架,并提出減小路面損傷的方法；王直民等[6]分析了車輛動荷載系數的概率分布,運用疲勞損傷理論得出了不平整路面上等效動荷載的表達式；舒富民等[7]研究了移動荷載作用下路面力學指標響應結果，分析了車速對各力學指標的影響規律；陳俊等[8]建立路面結構的離散元模型，模擬了靜止、振動和移動荷載對路面結構的作用，并分析出了不同荷載形式下路面結構的力學響應。

綜上所述，現有研究多數圍繞動載對路面結構的動態力學響應，未考慮影響動載作用大小的動載系數，筆者運用車輛-路面振動模型，推導車輛動荷載系數表達式，利用MATLAB數學分析軟件，計算振動矩陣方程，分析了在不同路面振幅、波長下，最大動載系數的變化規律，研究了懸架系統和輪胎剛度、阻尼對動載系數的影響。

1 產生動載的原因

振動，是車輛對路面產生動載的先決條件，而車輛實際行駛過程中產生振動是不可避免的。車輛的振動不僅會降低乘客的舒適度和安全性，同時也會增加汽車零部件的磨損及行駛燃料的損耗，最終由車輛振動產生的動載又會作用在路面上，進一步加劇路面的破壞。車輛行駛的過程，實質上是一個車輛與路面相互作用的過程，動荷載產生的原因也主要來自車輛和路面這兩個方面。一方面由于路面的不平整導致車輛產生各個方向的振動，振動主要為垂直路面方向；另一方面，車輛自身的振動。車輛內部的發動機的振動會引起車身間歇性振動。

2 動載系數表達式的建立

2.1 1/4車輛振動模型

在實際中，車輛是一個多自由度的復雜振動系統，所以建立車輛模型的自由度越多，模擬出的運動狀態就越真實。車輛是由一系列具有質量、剛度和阻尼特性元件的組合。為簡化計算，采用二自由度的1/4車輛模型作為振動模型，該模型只考慮車輛的豎向運動，即非懸架和懸架系統的豎向振動，忽略了其他各向的運動，如圖1。

圖1 1/4車輛振動模型

圖1中：m1為非懸架質量；m2為懸架質量；k1為非懸架剛度；k2為懸架剛度；c1為非懸架阻尼；c2為懸架阻尼；y1為非懸架垂直位移；y2為懸架垂直位移；y0為路面對車輛的激勵，即路面平整度函數。其運動微分方程為：

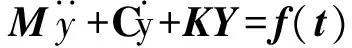
(1)

或：

(2)

式中：M為質量矩陣；C為阻尼矩陣；K為剛度矩陣；Y為位移列陣；f(t)為荷載列陣。

2.2 求解振動方程

東，表示日出的方向，與“西”相對，詩云：“嚖彼小星，三五在東。”(《詩·召南·小星》)西，則表示日落的方向，“自西徂東，靡所定處。”(《詩·大雅·桑柔》)“東西”最早出現時也表示方位，與“南北”相呼應。

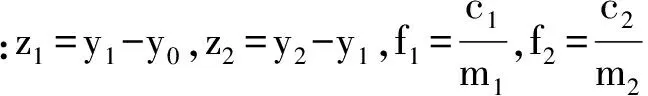
則：

(3)

利用待定系數法，設：

(4)

現階段對于路面平整度的表達，普遍采用MW. Sayers的正弦波路面表示方法，因此路面波形函數為：

y0=hsin(ωt)

(5)

式中：h為路面不平整度，即正弦波函數的振幅；ω為頻率，與車速和路面不平整度波長有關。

將z1，z2，y0帶入式(3)可寫成矩陣形式：

利用MATLAB求解器計算上面的矩陣方程，可以得出A1和A2，帶入式(4)得到z1，則車輪對路面的動荷載表達式為：

(6)

其中：

θ=tan-1(A1/A3)

當正弦函數sin(ωt+φ)=1時，pd得到最大值：

(7)

最終可以得出動荷載系數D：

式中：P0為車輛靜載，通常為(m1+m2)g。

3 動荷載系數的求解和分析

以中型標準車輛為分析對象，帶入車輛結構參數，通過MATLAB數學分析軟件，計算動載系數，分析路面不平整度、車輛參數等因素對最大動荷載系數的影響規律。標準車輛結構參數如表1。

表1 車輛結構參數

3.1 車速、路面不平整度對動荷載系數影響規律

如圖2，隨車速的增加，動荷載系數先減小后增大，到達峰值后略微下降。車輛在20～40 km/h低速行駛時，動荷載系數較小，主要在1.1～1.2范圍內變化，超過40 km/h后，動荷載系數大幅增加，大約110 km/h時，動荷載系數達到最大值1.47。可見，車速的變化對于動荷載系數的影響較大，應根據道路等級合理選取速度區間。

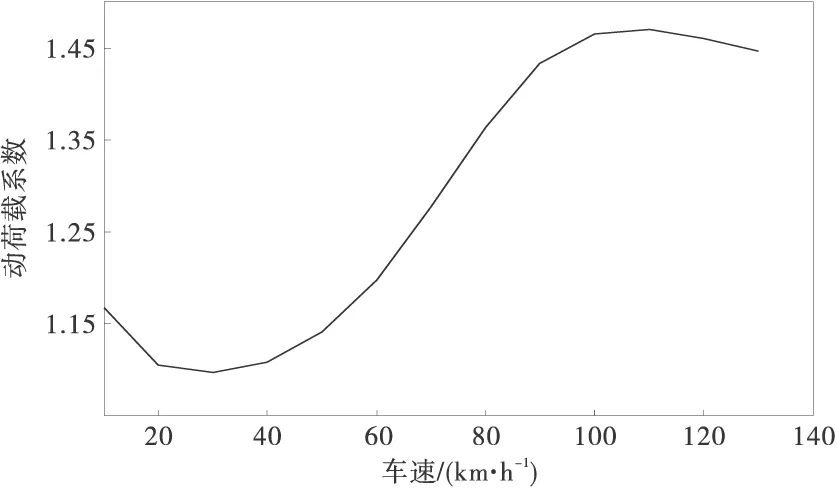
圖2 動荷載系數與車速的變化關系曲線

由圖3可以看出，隨著路面波長的不斷變大，動荷載系數呈現兩個波峰。第1個波峰的峰值略大于第2個波峰，當波長較小時，動荷載系數的第1個峰值可以達到最大值1.5。圖3有40，80，120 km/h 三個速度下的變化曲線，均呈現上述特征，而且速度的變化對動荷載系數的峰值影響很小。當波長增大到某一程度，可以當作路面趨于平整，此時動荷載系數接近于1。

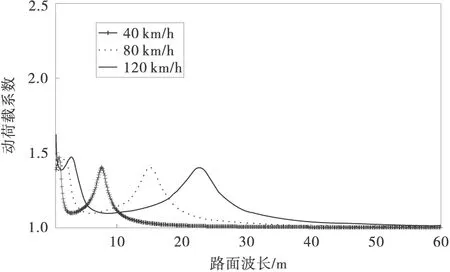
圖3 動載系數與路面波長變化關系曲線

圖4分別取車速為40，80，120 km/h，在不平整度由小到大依次變化。車速一定時，隨著路面振幅的增大，動荷載系數呈線性遞增，這與實際經驗相符，所以路面不平整度的幅值對動荷載系數的影響很大，控制路面平整度是減小動載的重要途徑。當振幅一定時，速度較大的，動荷載系數也變大，觀察曲線可以看出，速度大的，動荷載系數增速較快，這可以看作由路面不平整度所引起的振動與車輛自身振動相耦合，也就是說，速度變大會加劇車輛的振動，最終導致動荷載系數大大增加。

當實際路面狀況較差時，根據車速對動荷載系數的影響分析，應及時對該路段進行修補和交通管制，限制車輛行駛速度，不僅可以降低路面損壞程度，也提高了車輛行駛的安全性。

圖4 動荷載系數與路面振幅的變化關系曲線

隨著路面振幅的增大，動荷載系數呈線性遞增，這與實際經驗相符，從圖4可以看出，路面不平整度的幅值對動荷載系數的影響很大，所以控制路面平整度是減小動載的重要途徑。速度較大時，動荷載系數變化幅度增大，這可以看作由路面不平整度所引起的振動與車輛自身振動相耦合，也就是說，速度變大會加劇車輛的振動，導致動荷載系數大大增加。

3.2 車輛參數對動荷載系數的影響規律

由于車輛參數的影響因素較多，所以選取路面波長為3 m，路面振幅為0.01 m作為路面不平度條件作為前提，逐一分析各車輛參數對動荷載系數的變化規律。圖5是輪胎剛度對動荷載系數的影響規律。動荷載系數隨著輪胎剛度遞增，并且數值變化較大，當輪胎剛度增加70%時，動荷載系數會提高30%；而與上述過程截然相反的是，隨著輪胎阻尼的增大，動荷載系數會降低，但是影響的程度很小。如圖6輪胎阻尼從4 kN·s/m增大到8 kN·s/m，動荷載系數只變化了3%。

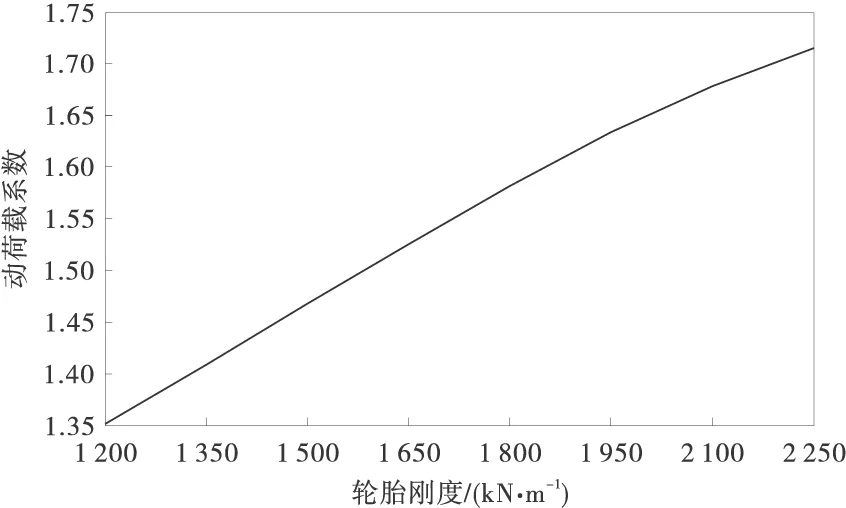
圖5 動荷載系數與輪胎剛度的變化關系曲線

圖6 動荷載系數與輪胎阻尼的變化關系曲線

圖7和圖8是懸架剛度和阻尼對動荷載系數的影響變化規律。很明顯，隨著懸架剛度和阻尼的增大，動荷載系數均減小。當懸架剛度和阻尼增加200%，動荷載系數分別降低了4%和5%，可見增加懸架的剛度和阻尼可以降低動荷載系數，減小車輛運行的振動，但是影響程度很小。

圖7 動荷載系數與懸架剛度的變化關系曲線

圖8 動荷載系數與懸架阻尼的變化關系曲線

在運行速度為80 km/h，車輛空載、滿載、超載10%，20%，30%，40%，50%，60%，70%，80%的條件下，計算動荷載系數的變化，如圖9車輛空載的動載系數較滿載時高10%左右，車輛振動較劇烈。隨著載重不斷增大，動荷載系數也逐漸減小。雖然在一定程度下，載重的增加可以減小動荷載系數，但是車輛靜載和附加動載總和會變大，對路面的沖擊力仍會大幅提高，路面很有可能產生嚴重的結構性破壞。所以，車輛應嚴禁超載，防止路面損害。

圖9 動荷載系數與載重的變化關系曲線

根據實際路面狀況，取中型標準車的結構參數，當路面不平整度h=0.02 m，路面波長為3 m，車速為80 km/h下，求出最大動荷載系數參考值為1.46，該值比普遍認為的1.3～1.4較大。當路面不平整度較差時，動載可以達到靜載的2倍、甚至3倍以上，所以當路面出現損壞時，必須及時修補或者采取交通管制，否則可能為道路、行車安全帶來重大隱患。

4 結 論

1)車輛在行駛過程中，由于路面不平整而產生對路面的附加荷載，這正是車路相互作用的結果。根據瀝青路面的特點，以正弦波形路面作為激勵，利用四分之一車輛振動模型，建立了車輛-路面動載系數計算模型。

2)以標準車輛為對象，通過MATLAB數學計算軟件，研究路面平整度、車速、載重及車輛參數對動荷載系數的影響規律。當車速較低時動荷載系數較小，速度超過40 km/h時動荷載系數與車速呈線性增長關系，速度達到110 km/h時，動荷載系數達到峰值；路面振幅對動荷載系數影響較大，這驗證了路面不平整是引起動荷載的主要原因。由于車速耦合作用明顯，當路面狀況較差時，應降低車速，及時修補，避免加劇路面的損壞。

3)輪胎剛度對動荷載系數影響較大，適當降低輪胎剛度可以減小動荷載系數。輪胎阻尼、懸架剛度、懸架阻尼的提高均可降低動荷載系數，但影響程度較小，可根據車輛構造，合理選取車輛結構參數。

4)根據實際道路狀況，動荷載系數基本在1.4～1.5范圍內，但出道路損壞時，動荷載系數將成倍增長。嚴格控制路面平整度是減小動荷載和道路損壞，提高道路使用壽命的重要途徑。

[1] Cebon D.Theretical road damage due to dynamic tire forces of heavy vehicles [J].Journal of Mechanical Engineering Science,1988,202(2):103-117.

[2] Siddharthan R V,Krishnamenon N,El-Mously Mohey,et al.Investigation of tire contact stress distributions on pavement response [J] .Journal of Transportation Engineering,2002,128(2):136-144.

[3] 鄧學鈞，孫璐.車輛-地面結構系統動力學[M].北京：人民交通出版社，2000. Deng Xuejun,Sun Lu.Dynamics of Vehicle-Ground Pavement Structure System [M].Beijing:China Communications Press,2000.

[4] 葉開沅,馬國琳.行動載荷作用下的連續梁的橫向振動問題[J].應用數學和力學,1985,6(10):873-878. Ye Kaiyuan,Ma Guolin.Vibration theory of continuous beam under the action of moving load [J].Applied Mathematics and Mechanics,1985,6(10):873-878.

[5] 余卓平,黃錫朋,張洪欣.減輕重型汽車對道路的損傷-汽車懸架優化設計[J].中國公路學報，1994,7(3):83-87. Yu Zhouping,Huang Xipeng,Zhang Hongxin.The alleviation of damage to road by heavy vehicle optimization design of vehicle suspension [J].China Journal of Highway and Transport,1994,7(3):83-87

[6] 王直民,張土喬,吳小剛.不平整路面上的車輛等效動載系數[J].浙江大學學報:工學版,2007,41(6):1007-1011. Wang Zhimin,Zhang Tuqiao,Wu Xiaogang .Equivalent vehicle dynamic load coefficient on rough pavement [J].Journal of Zhejiang University:Engineering Science,2007,41(6):1007-1011.

[7] 舒富民,錢振東.移動荷載作用下瀝青路面的動力響應分析[J].交通運輸工程與信息學報,2007,5(3):90-95. Shu Fumin,Qian Zhendong.Analysis on the dynamic response of asphalt pavement under moving Load [J].Journal of Transportation Engineering and Information,2007,5(3):90-95.

[8] 陳俊,黃曉明,汪林兵,等.移動荷載作用下柔性路面多尺度結構的響應[J].東南大學學報：英文版,2013,29(4):425-430. Chen Jun,Huang Xiaoming,Wang Linbing,et al.Dynamic response of multi-scale structure in flexible pavement to moving load [J].Journal of Southeast University:English Edition,2013,29(4):425-430.

Vehicle Dynamic Load Coefficient Analysis Based on Pavement Roughness

Yang Chunfeng, Xie Shuai, Sun Jishu

(School of Civil Engineering, Hebei University of Technology, Tianjin 300401, China)

In order to study the dynamic load effect of vehicle running on uneven pavement further, a quarter-vehicle vibration model was applied to analyze the influence law of dynamic load coefficient based on the pavement roughness, vehicle parameters and other factors by using MATLAB software. Calculation result indicates that speed and the road surface amplitude have a great influence on the dynamic load coefficient, and pavement amplitude has a linear relationship with dynamic load coefficient. It is also indicated that the main cause of the dynamic load is pavement roughness; tire damping, suspension stiffness and suspension damping have less impact on the dynamic load coefficient than others, meanwhile, to reduce the tire stiffness can significantly reduce the dynamic load. From the view point of road design, to improve the road roughness is an important measure to reduce the dynamic load.

road engineering; vibration model; vehicle parameters; dynamic load coefficient

10.3969/j.issn.1674-0696.2015.04.14

2014-04-23；

2014-10-14

河北省高等學校科學研究計劃項目(Q2012156)

楊春風(1959—)，男，天津薊縣人，教授，主要從事道路工程方面的研究。E-mail：cfy211@163.com。

U416.217

A

1674-0696(2015)04-077-04