基于數據分治與雙層索引的并行點面疊加分析方法研究

周 玉 科,周 成 虎，馬 廷，高 錫 章，范 俊 甫，許 濤，季 民

(1.中國科學院地理科學與資源研究所，資源與環境信息系統國家重點實驗室，北京 100101；2.山東理工大學建筑工程學院，山東 淄博 255049；3.山東科技大學測繪工程學院，山東 青島 266510)

?

基于數據分治與雙層索引的并行點面疊加分析方法研究

周 玉 科1,周 成 虎1，馬 廷1，高 錫 章1，范 俊 甫2，許 濤1，季 民3

(1.中國科學院地理科學與資源研究所，資源與環境信息系統國家重點實驗室，北京 100101；2.山東理工大學建筑工程學院，山東 淄博 255049；3.山東科技大學測繪工程學院，山東 青島 266510)

地圖疊加分析是一種計算密集型算法，并行化計算是加快算法執行速度的一種有效方法。該文研究分布式環境下的點面圖層并行化疊加分析方法與實現。首先根據點面疊加的特點設置并行數據分解的方式，基于分治法分解空間數據，在并行系統下將地理要素分而治之。然后引入雙層索引的并行疊加機制，一是對面圖層根據Hilbert空間索引的排序方式分發數據，二是對點圖層建立四叉樹索引，對每一個進行相交運算的多邊形進行快速過濾和求交。最后在Linux集群系統下實現該并行算法，其一利用MPI分布式計算環境實現在整體計算框架下的消息通訊模式的并行，其二在每個子節點中實現基于多核OpenMP工具的本地并行化。結果表明，利用雙層空間索引分治的方法可實現并行數據分塊，各子節點實現獨立計算，減少并行系統中的I/O沖突，并行加速比明顯。該方法對矢量地圖運算的并行化進行了有益的嘗試，為大數據時代的空間數據分析提供一種有效的途徑。

地圖疊加分析；并行計算；空間索引；MPI；OpenMP

0 引言

地圖疊加分析(Map Overlay)是GIS空間分析中最基礎、使用最頻繁的一種操作[1]，指同一地域范圍的兩個或多個地圖圖層在同樣空間參考系下進行疊加，獲取具有新屬性的空間區域并最終生成一個新的圖層，圖層要素屬性由疊加運算符決定，其本質過程是一系列計算幾何布爾操作和屬性傳遞過程的集合。圖層疊加中幾何對象之間的操作已被證明為時間復雜度最少為O(nlogn)的操作[2]，因此涉及全幅地圖圖層的疊加分析屬于計算密集型操作。點與多邊形圖層的疊加分析是其中基本的操作類型之一，其實質是點包含問題(單點或復雜對象組成點)。

隨著數據規模的日益膨脹、實時性應用的增加，對地圖疊加分析功能在計算效率、性能、處理能力等方面的要求也越來越高。并行計算技術從20世紀70年代隨著計算機體系架構的進步和成熟發展起來，由于并行技術發展時間不長，因此GIS的核心空間分析功能的并行化仍然處在迅速發展時期[3,4]。近年來，并行計算機的強大硬件加速特性和新的并發設計思想為解決復雜度日益增加的地學問題和海量級別的數據處理問題提供了新的解決方案，同時也為地圖疊加分析提供了理論和實踐基礎。點面疊加分析是地圖疊加分析中的一種基本操作，輸出結果判斷點被多邊形包含關系[5,6]。已有學者利用各種并行計算工具對地圖并行疊加分析進行探索，如利用GPU加速[7]和集群并行方法[8,9]。本文利用并行計算的基礎理論方法，重點研究在并行化地圖疊加分析中的靜態負載均衡方法，以數據并行為主線，利用Hilbert空間索引分解地理數據，達到各任務節點計算量基本平衡，各個節點再次進行細粒度并行判斷包含關系。

1 雙層索引方法與分治并行策略

1.1 并行疊加特征預分析

本文針對點圖層與面圖層的疊加分析，運算對象之間屬于多對多的關系，因此研究對象的粒度應該從點與邊的關系上升到點集合與多邊形集合之間的關系、點集內部的空間分布特征關系和多邊形集合之間的空間近鄰關系。傳統的并行算法設計考慮每個原子級別的操作并保證每個節點處理時間大致相同。如果按照傳統設計方法將點和多邊形相交降低維度將增加數據組織和計算的復雜度。假設點和多邊形數量均為n，采用直接求交方法的時間復雜度為O(n2)；如果將多邊形以邊為粒度進行分解，假設每個多邊形最少有m條邊，則計算的時間復雜度會上升到O(mn2)。為更好地提升圖層直接疊加效率，仍然從減少不必要耗時操作的原則出發，使用混合雙層索引分解的方法對點面圖層疊加進行預處理，以數據分治的方式實現并行。

圖層粒度級別的多邊形疊加分析更適合以面向對象的形式組織，根據并行計算的原理并行粒度越大獲得的加速比越大。從點圖層考察，點數據分布具有不規則性和不平衡性，因此必須加以約束減少疊加分析過程中不必要的包含測試。從GIS空間查詢分析的基本過程考察(圖1)，疊加分析算法可以獲得并行加速的階段主要在數據輸入輸出、過濾階段和圖元對象的精確幾何計算過程。

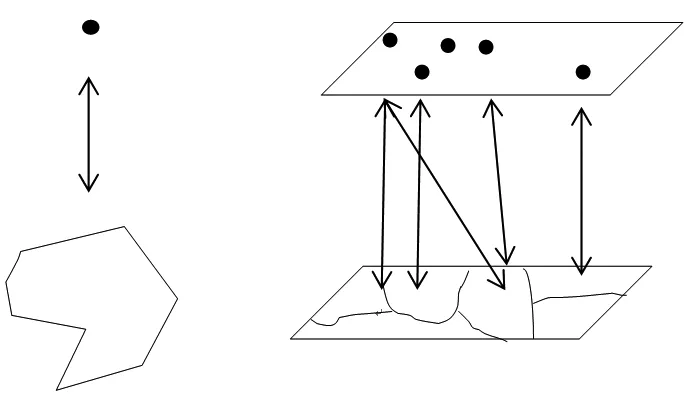
圖1 單對象關系和圖層多對象關系

Fig.1 Single object relationship and layer multi-object relationship

幾何圖形過濾階段的加速是點面疊加分析的關鍵步驟[10]，圖層級別的點與多邊形疊加分析并行化的基礎仍然是數據域分解和并發調度。本文的快速過濾是基于幾何圖形MBR的空間索引機制，MBR是包圍圖元且平行于X、Y軸的最小外接矩形在索引結構中用來代表真實幾何元素。首先需要考慮疊加圖層的特性，點圖層的元素無外包矩形或者以計算機默認容差為寬度(長度)設定的小方格，在空間查詢中小方格的相交計算明顯會增加計算量。因此對于點圖層采用四叉樹索引的機制，其生成規則為當每個單元格只有一個點時不再繼續遞歸劃分。因為單元格是獨占的，所以點圖層的索引沒有冗余節點。

按照二叉樹表示二維點數據的方法，該研究在此基礎上進行修改對點圖層構建四叉樹索引。點四叉樹與四叉樹具有同樣的特點，但是當對于次分區的中心總是在一個點時，點四叉樹被視為一個真樹(true tree)，樹的形態根據排序后的數據而定。對分布較規律的二維點的查詢具有較高的效率，通常的運行時間復雜度在O(logn)之內，基于點四叉樹構造空間索引的時間復雜度為O((n/2)logn)。

1.2 雙層索引的多級并行方法

在并行點面疊加分析中設置主動圖層和被動圖層的概念。主動圖層作為切割對象，被動圖層作為被切割對象。因為地圖系統是按照層次結構進行組織，有學者[11]已證明以點為基礎要素的地圖圖形系統和以地圖符號為基礎單元的地圖符號系統屬于布爾代數系，因此也說明地圖圖層系統也可以應用于計算機處理器內的邏輯運算。雖然邏輯上兩個圖層疊加都是相互作用的布爾操作，容易直觀地認為不存在疊加的順序問題，但是既然涉及電子計算機的運算邏輯，其運算效率便與順序存在一定的關系。例如，最樸素的點面圖層疊加分析方法是對兩個圖層內的要素建立兩層循環進行直接求交。從計算機內存使用和程序設計的策略衡量，對于嵌套的多層循環，外部循環量需要盡量大于內部循環量。因此在并行點面疊加的數據分解中以多邊形圖層作為主動圖層進行包含查詢。

從空間分布特點考慮，點數據圖層具有聚集特性，適宜采用四叉樹索引的方式。另外由于多邊形數據的復雜性要高于點數據的復雜性，其空間分布不規則，根據空間數據域分解的方法，多邊形圖層的并行分解也需要考慮空間聚類特性，以保證各節點計算的負載均衡，因此對多邊形圖層建立基于Hilbert曲線排序的索引結構。首先使用MPI偽代碼的形式對并行點面疊加進行描述(表1)。

表1 點面疊加的MPI偽代碼

Table 1 MPI pseudo code for point-polygon overlay

1．initializeMPI2．if(masterprocess){3． buildHilbertsortindexforpolygonlayer4． broadcasttheHilbertinternalinformationtoslavenode5．}else{6． mapthenumberofpointsinfeaturelayertoanarray7． getthenumberoftotalpoints8． buildquadtreeforpoints9． calculatetheindexofpoints10． receivethespecificHilbertinternalinformationaboutpolygon11． getpolygonbetweenHilbertinternalfromlocalspatialdatabase12． Loop{13． calculatepolygoncontainpoint}14． mpi＿sendresultpointtomasternode15． }16．finalizeMPI

圖層級別點面并行疊加分析的具體步驟如下：

(1)建立索引。首先數據分配采用全冗余的機制，主節點和子節點存儲相同的矢量數據。主節點主要負責數據信息的一致性維護、中間結果回收。主節點對面圖層分別建立基于內存的Hilbert空間索引，各子節點對所存儲的點數據建立基于內存的四叉樹索引。從索引結構在計算機中的存儲位置可將其分為內存式和外存式兩種[12]，訪問計算機的內、外存儲器一次所耗費的時間分別為30～40 ns和8～10 ms，因此研究采用高效的內存索引。在點面圖層的并行疊加算法中空間索引有兩個重要作用：一是空間數據域分解的需要，達到數據的分治和計算的負載均衡；二是幾何對象進行相交判斷時快速確定相交粗集，減少不必要的真實求交操作。兩種方式中索引的功能都是空間查詢，并且使用次數較少、周期較短，因此采用內存索引的方式能夠達到快速高效的目的。

(2)多邊形分配。數據處理階段主節點對運算數據進行內存式空間索引，以多邊形圖層為主動查詢圖層，各節點進行數據本地化。有兩種策略實現數據本地化，一種是分析前在每個節點預部署一份相同的數據，另一種是通過掛載共享文件系統實現數據協同訪問。主節點將多邊形圖層按照Hilbert編碼排列順序，并將劃分好的序列片段發送到各子節點。本研究采用Hilbert曲線既可以保持多邊形的空間鄰近性，又能夠避免多邊形的分配存在冗余情況(圖2)。在不考慮多邊形鄰近性的情況下，使用多邊形要素FID劃分同樣能夠達到分治的效果，但許多地圖被編輯后(刪除、插入)，FID會出現不連續現象，無法保證數據分發的成功率，所以方法選擇空間和數列上均連續的Hilbert曲線編碼進行多邊形分配。排序劃分好的數組采用MPI_Send命令發送到指定子節點，各子節點接受后作為數據讀取時的過濾條件只抓取部分數據。

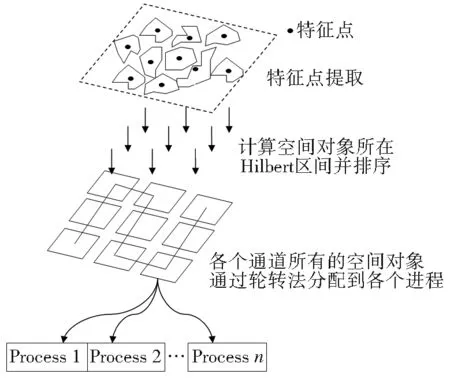
圖2 多邊形索引分發方法

Fig.2 Index and distribution method of polygon

(3)索引層快速過濾。在主節點將多邊形的索引標識平均分配到各子節點以后，子節點開始實際的疊加運算。首先各個節點加載本地數據，點圖層作為被動圖層需全部加載，同時需對其建立基于內存的四叉樹索引(圖3)。多邊形圖層按照主節點分配的標識提取圖層中的部分多邊形。索引層的快速過濾在多邊形的MBR和點四叉樹之間直接進行雙層循環，快速查詢與MBR相交的四叉樹節點。按照疊加順序的分析，多邊形MBR作為外層循環，點四叉樹作為內部循環，其中矩形間的碰撞檢測如圖4所示。多邊形MBR首先會與高層次的樹節點求交，然后依次遍歷該層次下面的子節點，以發現相交的底層葉子節點為終止條件。這些葉子節點被提交，并準備做下一步的精確包含測試。

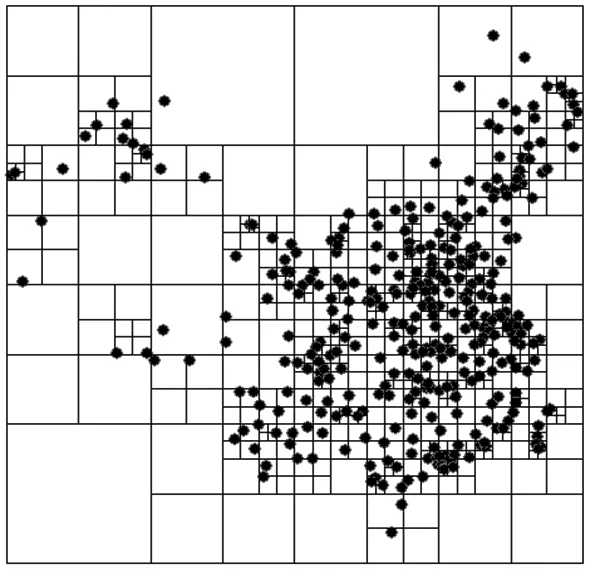
圖3 中國城市四叉樹索引

Fig.3 Quadtree index for cities in China

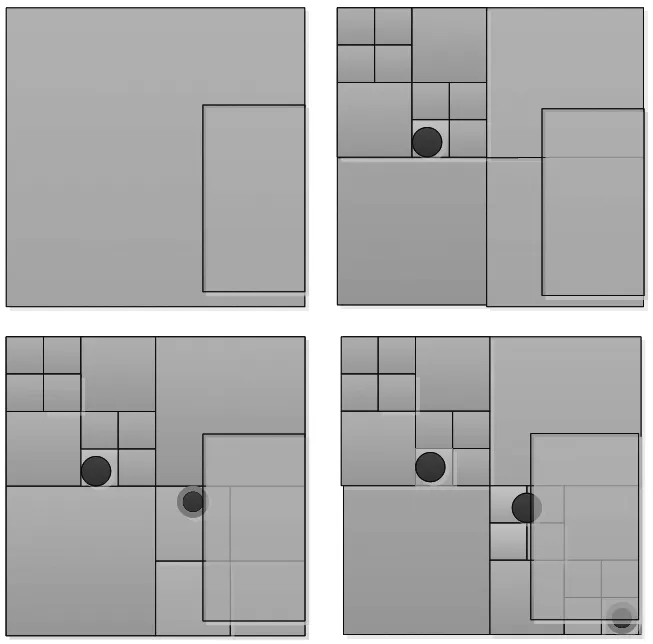
圖4 MBR查詢點圖層四叉樹示例

Fig.4 Query quadtree using MBR

圖4中矩形查詢的過程分為：1)查詢框與Level1節點相交，但是Level1中并不包含具體點對象。2)查詢框與Level2中節點相交，同樣Level1中也不包含點對象，但是其子節點需要進一步檢測。3)查詢框與Level3中的4個索引節點相交，并且包含一個點對象，將該點追加到輸出列表。右上的Level2節點沒有分裂生成Level3節點，因此不必進一步查詢。4)進一步查詢發現查詢框與6個Level4的節點相交，并在其中一個節點發現另一個點。因為剛發現的點在網格邊上，所以被劃歸為Level3層次的點。

查詢實驗共探測到2個點，其中一個在Level1線上，雖然該點沒有與查詢框明顯碰撞，但是仍然需要返回。實際運算中有大量點的情況下該判斷方法作為規則執行。以上四叉樹查詢結果是多邊形MBR所包含的點，如果不使用四叉樹空間索引查詢，可以利用MBR快速排斥達到同樣的效果(圖4)，但是查詢效率相對較低。四叉樹查詢的計算復雜度為O(logn)，而MBR直接過濾方法的計算復雜度為O(n)，因此采用效率較高的索引查詢方式。

(4)精確包含測試。在以上預處理工作的基礎上，多邊形MBR外的點已經被過濾掉，本階段將進行逐步求精的工作。精確求交過程既可以直接利用典型的winding-number包含算法實現，也可以采用本文設計的多核并行方法進一步加速疊加過程。當集群中存在大規模的并行節點時，因為節點間的通訊量呈平方級別的增長，所以隨著計算中間結果的通信增加帶寬將成為瓶頸。一種增加程序效率線性的方法是用MPI/OpenMP混合編寫并行部分。本算法設計的基本原則是MPI負責粗粒度的并行代碼，OpenMP負責細粒度迭代部分的并行。設計思路是每個節點分配1～2個MPI進程后，每個MPI進程執行多個OpenMP線程。OpenMP部分由于不需要進程間通信，直接通過內存共享方式交換信息，因此可以顯著減少程序所需通訊的信息。

結合以上多核算法與MPI算法，混合編程模式下的點面包含并行算法設計過程如下：1)使用初始化函數MPI_Init()啟動MPI程序；2)在MPI任務內啟動OpenMP并行程序；3)主進程或者MPI子進程串行執行；4)MPI的進程標記被所有OpenMP線程共享；5)串行和并行區域調用MPI庫；6)使用MPI_Finize()終止MPI程序。

本文的點面圖層并行疊加分析方法中MPI主要負責分發多邊形要素的標記id，然后啟動子節點程序載入數據并開始計算。子節點對點圖層建立四叉樹索引、外包矩形查詢過濾過程無法并行化。最后階段的精確包含測試可以是并行算法也可以是串行算法，將被封裝成一個函數供該過程調用。單個多邊形對象的并行測試方法中含有大量的同步操作和數據調度，因此為保證算法的整體穩定性，在圖層級別的并行時采用串行的測試方法。

(5)結果回收和輸出。子節點將真正包含測試后的結果發送給主節點，主節點負責接收并寫入新圖層。子節點不必發送真實的點要素數據，只需要發送包含點的fid標記數組。主節點接受后在本地圖層抽取數據，減少數據的傳輸和消息接收的排隊周期。各子節點均采用阻塞式發送，在確保主節點正確接收數據后返回消息。子節點發送中間結果說明本地計算已經完成，不需要考慮通信和計算的重疊問題，因此阻塞形式比較適合該情況。非阻塞形式的MPI通信可以實現計算與通信的重疊，但是在復雜計算中無法保證執行情況的正確反饋[13]。

2 實驗與分析

2.1 多核并行實驗

首先采用多核并行的方式進行實驗，實驗數據為全國土地利用圖(圖5)和POI興趣點(表2)。圖6為全國土地利用圖與全國POI點并行疊加加速效果，從統計圖可以看出其中并發線程間的動態調度方法加速效果明顯優于靜態調度方法。數據量增加引起單線程運行時間增加到6.9 s，在線程數達到8時，實際最大加速比為5.0，在一定程度上可以驗證“并行數據粒度越大加速比越大”的正確性。在線程數大于4時，動態調度策略的加速比呈現明顯上升趨勢，說明多線程并發的點面疊加可以獲得較好的加速效果。

圖5 疊加多邊形(土地利用分類數據)

Fig.5 Overlay polygon data

表2 疊加數據特征

Table 2 Features of overlay data

數據源名稱數據類型要素數量線段數量點數量土地利用圖多邊形15615648894886547全國導航POI點點463142083142

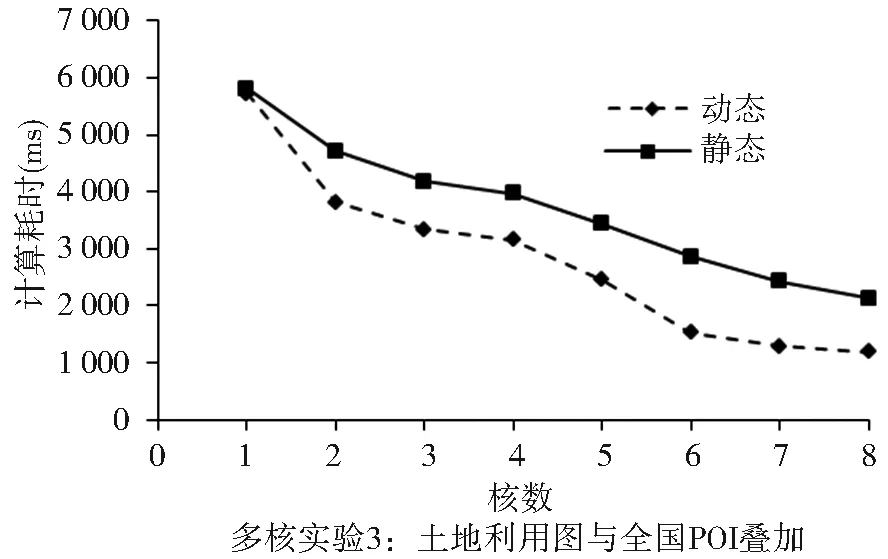
圖6 多核并行加速實驗計算時間

Fig.6 Computing time for multi-core paralleling computing test

2.2 MPI并行實驗

按照上文MPI形式的并行點面疊加算法設計，在IBM高性能集群中對該算法進行實驗。實驗環境為6臺機架式服務器，所有機器操作系統均為Redhat6.2(Linux Kernel2.6.40)，其中一臺4*6核機器作為主節點，其他節點作為子節點。空間數據存儲策略為每個節點維護一個全局的矢量數據庫，主節點發送主動疊加圖層的分解信息，各節點獨立進行主動圖層(多邊形)數據抽取，然后并行的對點圖層實現包含測試。

MPI并行點面包含疊加實驗以數據量較大的土地利用圖和全國POI點為處理對象，分別采用1～12個進程測試并行加速情況。測試實驗效果如圖7所示，從中分析不同進程的加速情況可以看出，在計算進程不超過總體物理節點數量6時加速效果比較明顯，原因是在輪詢式的進程任務分配情況下每個物理節點最多只運行一個進程，不存在同節點間進程的重疊，因此對本地數據庫訪問和CPU的消耗都比較小。MPI單進程時計算用時為5 382 ms，在12個進程時用時為893 ms，加速比從1上升到6.0。從1個進程到2個進程時的加速效果最高，變化范圍為1～1.62。從加速比的統計圖可看出多機多進程情況下基本可以達到疊加的線性加速(圖8)。

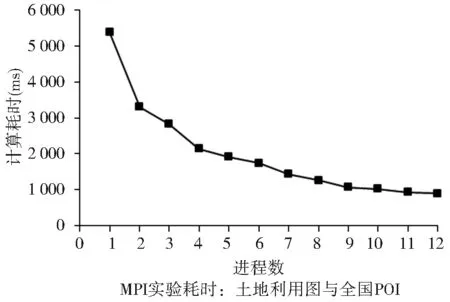
圖7 MPI并行點面疊加實驗計算耗時情況

Fig.7 Computing time for MPI test

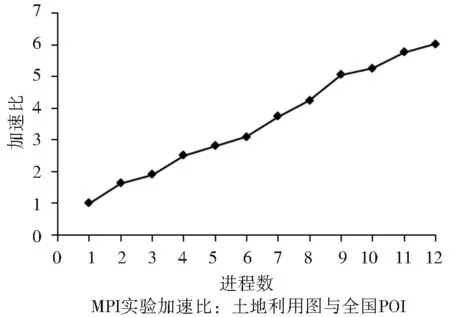
圖8 MPI并行點面疊加實驗加速比情況

Fig.8 Speedup for MPI test

對比單機多核與多機器集群的并行方式可以發現，單機環境下開啟多核計算得到的加速效率低于集群環境下多節點并行計算的加速效率。除單機CPU計算核心數量的限制外，OpenMP多核編程的共享內存方式對于粗粒度的并行對象讀寫沖突情況較多；另外重要的一點是單機環境下的數據集中式存儲方式本身對并行計算的算法有較大限制，主線程啟動的多個子線程無法同時在同一塊物理磁盤上進行數據讀寫操作，導致數據并發訪問成為瓶頸，而集群環境下的多節點分布式存儲方式則可以有效地避免該問題，提高了執行效率(圖9)。從加速效率上對比，MPI集群并行情況下的加速效率與多核并行情況下的動態負載策略基本相同，但是二者加速效率均明顯高于OpenMP靜態調度策略。從并行運行的時間分析，MPI并行時間少于多核并行策略，并且數據量越大加速效果越明顯。

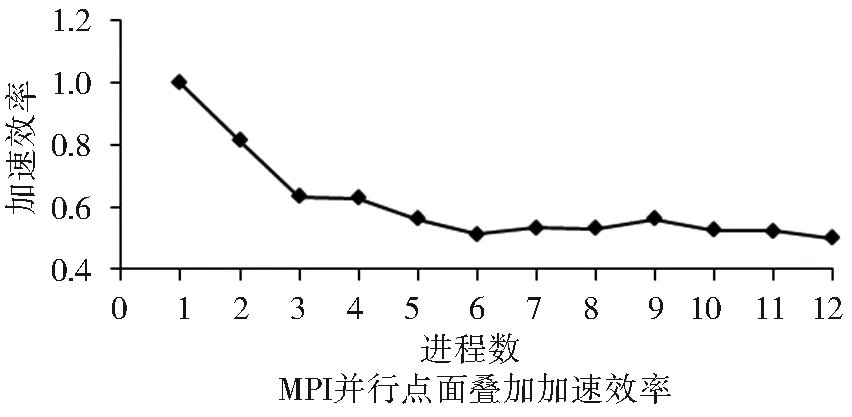
圖9 MPI并行點面疊加實驗加速效率

Fig.9 Speedup efficient for MPI test

3 結論

本文研究了分布式環境下點面疊加分析的在的并行化方法與實現。采用Hilbert空間索引的方式進行多邊形數據的分發，各個計算節點經過快速四叉樹和MBR過濾后進行點面疊加分析。雙層索引以空間排序作為數據分解的依據，提高了各計算節點的運算效率(減少多邊形與點的無效疊加)。分析實驗結果可以得出針對點面疊加并行運算的結論：多核并行疊加和MPI集群疊加方法均可以有效地加速點面包含測試操作，不同規模和形式的處理數據應選擇不同的策略：在點與面圖層要素數量較大時，適宜采用MPI消息傳遞形式的集群并行策略，數據量較小時采用多核并行的策略，并且調度策略使用動態調度時加速效果較好。因為在數據量比較小時，MPI需要主節點進行集群環境的初始化、數據的預分解處理和分解信息分發，對于數據量較小的點面疊加這些初始化過程占用時間比例較大，只有數據量達到一定的規模集群才能夠充分發揮計算功能。該方法可以實現并行計算中的數據負載均衡，減少數據沖突，并行加速效果明顯，可以作為一種地學并行計算模式探討其他空間分析方法的并行化。

[1] KRIEGEL H P,BRINKHOFF T,SCHNEIDER R.An efficient map overlay algorithm based on spatial access methods and computational geometry[C].Proc.Int.Workshop on DBMS′s for Geographical Applications,1991.

[2] DING Y,DENSHAM P J.Spatial strategies for parallel spatial modelling[J].International Journal of Geographical Information Systems,1996,10(6):669-698.

[3] 吳立新,楊宜舟,秦承志,等.面向新型硬件構架的新一代GIS基礎并行算法研究[J].地理與地理信息科學,2013,29(4):1-8.

[4] 王結臣,王豹,胡瑋,等.并行空間分析算法研究進展及評述[J].地理與地理信息科學,2011,27(6):1-5.

[5] 謝忠,葉梓,吳亮.簡單要素模型下多邊形疊置分析算法[J].地理與地理信息科學,2007,23(3):19-23.

[6] 張樹清,張策,楊典華,等.簡單要素模型下的多邊形對象疊加并行運算策略研究[J].地理與地理信息科學,2013,29(4):43-43.

[7] 趙斯思,周成虎.GPU加速的多邊形疊加分析[J].地理科學進展,2013,32(1):114-120.

[8] 范俊甫,馬廷,周成虎,等.分治法在GIS多邊形快速合并算法中的應用及效率提升評價模型[J].地球信息科學學報,2014,16(2):158-164.

[9] 周玉科,馬廷,周成虎,等.MySQL集群與MPI的并行空間分析系統設計與實驗[J].地球信息科學學報,2012,14(4):448-453.

[10] 朱效民,趙紅超,方金云.魯棒高效的矢量地圖疊加分析算法[J].遙感學報,2012,16(3):448-465.

[11] 鐘業勛,朱重光,魏文展.地圖空間認知的數學原理[J].測繪科學,2005,30(5):11-12.

[12] 張明波,陸鋒,申排偉,等.R樹家族的演變和發展[J].計算機學報,2005,28(3):289-300.

[13] 胡曉力,田有先.多粒度并行計算集群研究與應用[J].電力學報,2008,22(4):436-438.

A Double-Index and Data Divide-Conquer Based Parallel Point-Polygon Overlay Method

ZHOU Yu-ke1,ZHOU Cheng-hu1,MA Ting1,GAO Xi-zhang1,FAN Jun-fu2,XU Tao1,JI Min3

(1.LREIS,InstituteofGeographicSciencesandNaturalResourcesResearch,CAS,Beijing100101; 2.SchoolofArchitecturalEngineering,ShandongUniversityofTechnology,Zibo255049; 3.CollegeofGeomatics,ShandongUniversityofScienceandTechnology,Qingdao266510,China)

Map overlay analysis is a computing intense algorithm,so it is straightforward that parallel computing algorithms can speed up the executing efficiency.The paper aims to study the method and implement of the parallel point-polygon overlay analysis in a distributed computing environment.Firstly,according to the characteristic of point-polygon overlay analysis,spatial data decomposition method is designed to make parallel available on the basis of spatial index.Then geographical data is processed by using the divide-conquer method on a parallel computing system.In this parallel point-polygon overlay method,double layer index mechanism is applied in order to accelerate the query process in geometry overlay step.On the one hand,the polygon layer is indexed and sorted by Hilbert space-filling curve,and then the data can be distributed to every computing node.On the other hand,point layer is indexed by quad-tree structure in order to speed up the query and filter process executed by every polygon.Finally,this parallel method is implemented on a Linux based cluster system.Coarse-grained task is paralleled using the MPI cluster-computing tool,and on every computing node the fine-grained task is paralleled using the OpenMP multi-core paralleling computing tool.The results show that this parallel point-polygon overlay method is able to reduce the I/O conflicts and every node is independent in computing process,from which apparent speedup is obtained.This work can give a new insight in map overlay analysis,meanwhile it provides a meaningful way for computing pattern of GIS data in the big data era.

map overlay;parallel computing;spatial index;MPI;OpenMP

2014-08-13；

2014-10-27

中國科學院重點部署項目(KZZD-EW-07)；山東科技大學科研創新團隊支持計劃項目(2011KYTD103)

周玉科(1984—)，男，博士后，從事高性能地學計算、空間分析研究。E-mail:zyk@lreis.ac.cn

10.3969/j.issn.1672-0504.2015.02.001

P208

A

1672-0504(2015)02-0001-06