高中數學中知識交匯試題的處理方法
穆雪霞
石家莊市第二十三中學
高中數學中知識交匯試題的處理方法
穆雪霞
石家莊市第二十三中學
高中數學知識交匯試題的出現不僅是高中數學學科特征發展的需要,也是提高學生綜合分析能力的關鍵。近幾年的高考中,數學知識的交匯問題出現的頻率越來越高。高中數學知識交匯問題出現的原因及怎樣解決這類題的教學方法已經成為一線教師迫切需要解決的問題了。下面,筆者就結合多年的教學實踐和經驗來談談自己的一些想法與做法。
高中數學;知識交匯;處理方法
一、高中數學知識交匯問題出現的原因
1、學科特點發展的需要
高中數學是一門科學的、嚴密的自然科學知識,所以,數學學科的系統性和嚴密性決定了數學知識之間深刻的內在聯系,它包括各部分知識的縱向聯系和橫向聯系。所以說,高中數學知識交匯問題的出現是學科特點發展的需要。
2、高考命題發展的需要
研讀《普通高等學校招生全國統一考試大綱》,不難發現:《大綱》一方面突出并強調了對主干知識以及知識和知識之間相互交匯與綜合的考查,另一方面向我們昭示了“在知識網絡交匯點處設計試題”,由此可見,高中數學知識交匯問題是新課程背景下必將堅持的高考命題方向。
二、走出高中數學知識交匯問題的誤區
高中數學知識交匯問題其實就是把兩個或幾個有關的知識點結合起來,全面地考察學生能力的一種綜合性試題。所以說,高中數學知識交匯問題絕對不是高中數學知識之間的機械的拼湊。
三、高中數學知識交匯問題的類型
高中數學知識交匯問題的類型有多種多樣,下面,就從兩個大方面來說說其類型:
1、傳統知識點之間的交匯
向量與三角交匯;向量與解析幾何交匯;向量與數列交匯;導數與函數、不等式交匯;導數與數列;導數與三角交匯;數列與函數交匯;數列與解析幾何交匯;概率與數列交匯;立幾與導數、概率交匯。
2、新增知識點的交匯
以算法為主線的交匯;以概率(幾何概型)為主線的交匯;以線性規劃為主線交匯。
四、高中數學中知識交匯試題的處理方法——以數列的交匯為例
數列作為一種特殊的函數,是反映自然規律的基本數學模型。新課程強調用函數的背景和研究方法來認識、研究數列,體會數列的函數背景,感受數列是研究現實問題情境的數學模型。接下來,舉幾個實例來闡述。
1、數列與函數的綜合
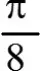
①、求證:y1+y2為定值;
③、在②的條件下,若
(n∈N*),Tn為數列{an}的前n項的和,若Tn<m(Sn+1+1)對一切
n∈N*都成立,試求實數m的取值范圍。
試題分析:本例題就是一個比較典型的數列與函數交匯的問題,在解決整個問題中,用到了函數問題、數列問題、中點問題、倒數相加問題、參數分離問題等。雖然是一個題,但是涉及的知識點卻是方方面面。
方法總結:數列與函數交匯問題的常見類型及解法
(1)已知函數條件,解決數列問題,此類問題一般利用函數的性質、圖象研究數列問題。
(2)已知數列條件,解決函數問題,解決此類問題一般要充分利用數列的范圍、分式、求和方法對式子化簡變形。另外,解題時要注意數列與函數的內在聯系,靈活運用函數的思想方法求解。
2、數列與不等式的綜合
典型例題:(2013·寧波模擬)設公比大于零的等比數列{an}的前n項和為Sn,且a1=1,S4=5S2,數列{bn}的前n項和為Tn,滿足b1= 1,Tn=n2bn,n∈N*.
(1)求數列{an},{bn}的通項公式。
(2)設cn=(Sn+1)(nbn-λ),若數列{cn}是單調遞減數列,求實數λ的取值范圍。
試題分析:(1)數列{an},{bn}的通項公式的求解思路:
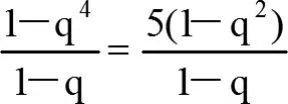
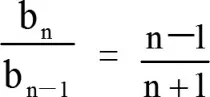
方法總結:證明與數列交匯的不等式問題的常用方法
(1)作差比較法證明。
(2)判斷數列的單調性,根據數列的取值范圍證明。
(3)合理利用放縮法證明。
高中數學知識交匯問題的類型有多種多樣,在此只是列舉數交匯的問題,選取的例題多是高考模擬試題和典型試題。解法和試題分析及規律總結有自己的觀點,也有別人的成果。不足之處,望給位同仁批評指教。
[1]喻波.運用數學思想方法發展學生思維能力[J].成都教育學院學報,2001(06).
[2]陳克勝.基于數學文化的數學課程再思考[J]數學教育學報,2009(01).
穆雪霞(1981-),女,籍貫:河北省邢臺市;單位:石家莊市第二十三中學。

