基于廣義S變換與雙向2DPCA的軸承故障診斷*
李巍華, 林 龍, 單外平
(華南理工大學機械與汽車工程學院 廣州,510640)
基于廣義S變換與雙向2DPCA的軸承故障診斷*
李巍華, 林 龍, 單外平
(華南理工大學機械與汽車工程學院 廣州,510640)
將軸承故障診斷問題轉化為故障信號時頻圖像的識別問題,提出一種采用雙向二維主成分分析(two-directional,two-dimensional,principal component analysis,簡稱 TD-2DPCA)的時頻圖像矩陣特征提取方法。首先,利用廣義S變換將軸承故障信號變換為時頻域圖像,采用一種雙向壓縮的二維PCA方法對圖像信息進行特征提取;然后,進行了軸承故障試驗,分別采集了軸承在正常、內圈故障及外圈故障狀態下的振動信號,采用所述方法對軸承3種狀態下的時頻分布圖像進行特征提取,并根據集成矩陣距離(assembled matrix distance,簡稱AMD)實現圖像的分類識別。試驗結果表明,結合廣義S變換的雙向2DPCA特征提取算法可有效提高計算效率,同時具有良好的診斷性能。
廣義S變換; 二維主成分分析; 圖像識別; 特征提取; 故障診斷
引 言
在以振動信號為參量的旋轉機械狀態監測和故障診斷中,由于轉速不穩定、負荷變化以及因故障產生大量的沖擊、摩擦等狀況,故障信號往往表現出較強的非線性和非平穩性。小波分析、短時傅里葉變換、維格納分布等時頻分析技術已廣泛應用于機械設備故障診斷領域[1-2]。S變換作為一種較新的時頻分析方法,結合了短時傅里葉變換和小波分析的特點,采用調諧的高斯窗函數,在低頻處有較高的頻率分辨率,在高頻處有較好的時間分辨率[3],是一種多尺度的時頻分析方法。采用時頻變換的實質就是將獲得的時域振動信號轉化為時頻圖像,由于時頻圖像包含了豐富的設備狀態信息,可以通過分析圖像實現故障的特征提取和智能診斷。同時為了克服圖像維數巨大導致的運算時間長、識別準確率低等問題,需要對圖像進行進一步的特征提取。
特征提取的本質是一個降維的過程。圖像以矩陣的形式存儲和表示,可通過矩陣理論實現圖像的壓縮。常用的方法有主成分分析(principal component analysis,簡稱PCA)、線性判據分析(linear discriminant analysis,簡稱LDA)、非負矩陣分解(non negative matrix factorization,簡稱NMF)等。PCA和LDA方法的共同缺點是降維前需將二維的圖像矩陣向量化,不能直接處理圖像矩陣[4]。Yang等[5]提出二維主成分分析(two-dimensional PCA, 簡稱2DPCA),并將其應用于人臉圖像的壓縮和重構,取得了良好的效果。Li等[6]在LDA算法的基礎上提出二維線性判別分析(two dimensional linear discriminant analysis,簡稱2DLDA),并將其與2DPCA方法的特征提取性能進行對比。這兩種方法直接使用原始圖像矩陣計算其協方差矩陣,不需將圖像矩陣向量化,優點是特征提取效率高,占用存儲空間少,已廣泛應用于人臉識別、圖像處理等領域[7]。其在故障診斷領域的應用還較少,目前有學者提出將2DLDA用于齒輪故障診斷當中[8]。此外,文獻[9-10]提出將NMF方法應用于齒輪和軸承時頻圖像矩陣的特征提取。同時,為克服矩陣向量化的缺陷,有學者提出采用2DNMF方法,提高了故障診斷的計算效率[11]。
2DPCA雖然能有效地降低圖像維數,但其數據壓縮是單向的,降維后的圖像特征可能依然較大。如一幅大小為m×n的圖像,經特征提取后變為m×d,列數減少,但行數不變,即圖像只在橫向進行壓縮。若m較大,對圖像進行向量化后的維數可能依然很高。因此,可用2DPCA方法對圖像先作一次橫向壓縮,對抽取出的特征矩陣再用一次2DPCA方法進行縱向壓縮,這樣就能大大地降低圖像維數。筆者采用一種結合廣義S變換和2DPCA的時頻圖像雙向壓縮提取特征方法用于軸承故障診斷。通過廣義S變換獲取時頻圖像,并對圖像矩陣利用雙向2DPCA(two-directional 2DPCA,TD-2DPCA)方法進行特征提取,最后采用集成矩陣距離(AMD)進行分類,對比2DPCA算法、2DNMF算法及2DLDA算法,分析其計算效率及分類性能。
1 廣義S變換及雙向2DPCA算法
1.1 廣義S變換
信號x(t)的一維連續標準S變換(簡稱S變換)定義如下
(1)
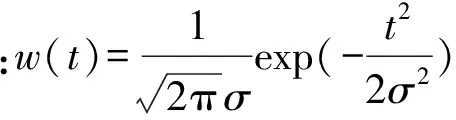
高斯窗既是時間也是頻率的函數,這就使窗函數在低頻處提供了較好的頻率分辨率,在高頻處可獲得較好的時間分辨率。文獻[3]指出,S變換是對連續小波的一種相位修正,這是常規小波變換所不具備的特性。因此,S變換是一種結合了短時傅里葉變換和小波分析優點的多尺度分析方法。

(2)
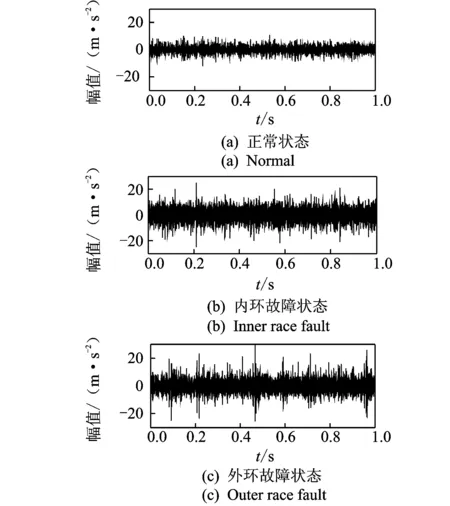
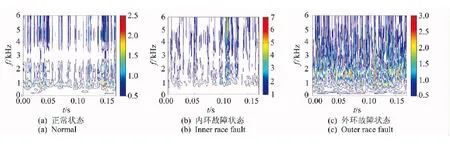
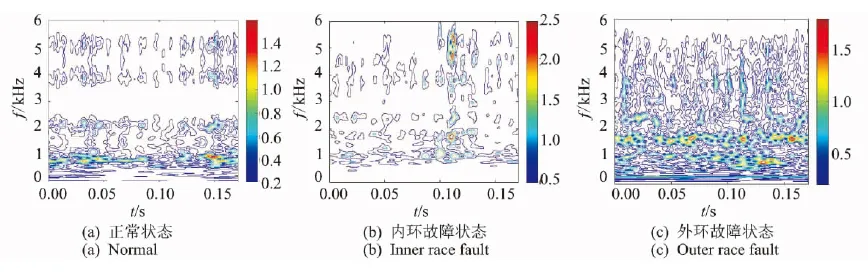
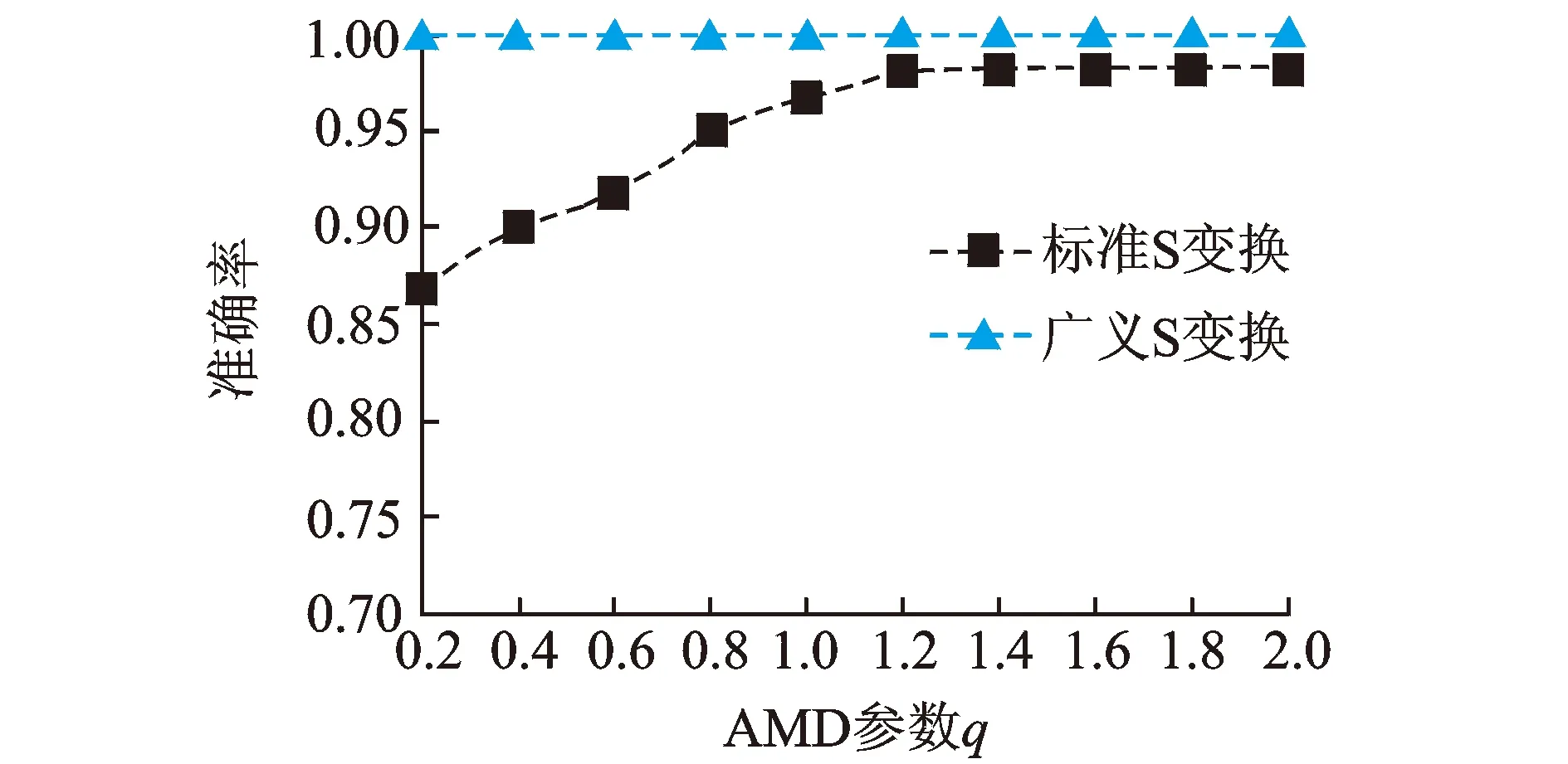
其中:參數p被限定為0 當p=1時,即為標準S變化;當p取負值時,窗寬隨著頻率的增加而增大,從而削弱對高頻信號的描述能力;當p>1時,又會使窗口在時域過窄,同樣不利于低頻信號的表達。通過尋找一個合適的p值,就能獲得較好的時頻分析效果。 為實現參數p的選擇,定義聚焦性度量值M(p)[13]為 (3) M(p)越小說明廣義S變換的時頻聚焦特性越好,可選擇最小M(p)對應的p值作為最優參數。文獻[14]以某典型非平穩合成信號進行仿真分析,仿真信號包含兩個線性調頻信號、兩個高頻沖擊信號和一個指數調頻信號,確定較優的p值為0.76。由于該信號體現了故障軸承信號的特點,如瞬時性(高頻沖擊成分)、分布頻率范圍寬(固有頻率成分)、存在調制現象等,筆者在后續軸承故障信號分析中,取廣義S變換p值為0.76。 1.2 雙向2DPCA算法 2DPCA本質是對圖像進行橫向壓縮,基本思想是以圖像的總體分散程度為目標,通過尋找一組最優的單位正交投影向量作為最優投影向量組,從而實現圖像的特征提取[15]。 假設有C類模式:w1,w2,…,wc,總共M個訓練樣本圖像:A1,A2,…,AM,每個大小為m×n。模式的總體散布矩陣Gt為 (4) 通過線性變換Y=AiX(i=1,2,...,k)將圖像矩陣Ai投影至X上,從而獲得特征向量Y。其中:X為n維單位化的列向量;Y為投影后的特征向量。投影方向X的選取準則是使得投影后的特征向量具有更好的可分性。定義準則函數 J(X)=tr(Gt)=XTGtX (5) 為了實現準則函數J(X)的最大化,需要尋找最優投影向量X。事實上,最優投影向量即為Gt的最大特征值所對應的單位特征向量。因Gt為非負定矩陣,則有n個標準正交的特征向量,假定 (6) (7) (8) 特征矩陣U向量化后的維數為h×d,而第1次提取出的特征維數為m×d,這樣h遠小于m,從而減少提取的特征維數,進一步提高分類效率。 1.3 AMD距離度量方法 特征提取后,不同的分類方法對識別率有一定的影響。可通過距離來度量不同類別,常用的距離度量方法有歐式距離、馬氏距離、相關系數距離等。文獻[16]給出了14種距離用于人臉圖像特征的分類。Zuo等[17]對適合2DPCA的矩陣距離度量進行了研究,給出了一種AMD矩陣距離。AMD距離定義如下 (9) 其中:A=(aij)m×d和B=(bij)m×d為2DPCA提取的特征矩陣。 當q=2時,AMD距離即為Frobenius距離,當q=1時,為Yang距離。 2.1 試驗設置 試驗模擬了齒輪箱軸承在不同狀態下的運行狀況,試驗臺由交流電機、齒輪減速機、轉速扭矩傳感器、聯軸器、二級齒輪箱及電磁加載裝置組成,如圖1(a)所示。加速度傳感器分別布置在齒輪箱輸入軸的前后端軸承蓋上,位置如圖1(b)所示。齒輪減速機速比為3.15∶1,故障軸承型號為Nu204,位于齒輪箱輸入軸末端,尺寸參數見表1。設置內環、外環兩種故障類型,采用線切割分別在外環加工寬1 mm、深2 mm 的細槽,在內環加工寬0.5 mm,深0.5 mm的細槽。試驗時,電機轉速恒定為1 502 r/min,設置載荷為60 Nm,采樣頻率為12 kHz,分別采集軸承在正常、內環故障、外環故障3類狀態下運行的振動信號,每類狀態40段信號樣本。根據表1軸承幾何尺寸,可計算內環故障特征頻率fi= 52.5 Hz,外環故障的特征頻率fo=35.5 Hz。 圖1 試驗系統組成Fig.1 Configuration of test system 表1 滾動軸承Nu204基本參數 Tab.1 Parameters of rolling bearing Nu204 節徑Dm/mm滾珠數/個滾子直徑d/mm接觸角/(°)33.5116.50 2.2 軸承不同運行狀態分析 圖2 時域信號Fig.2 Time domain waveform of bearing vibration signal 以測點1采集的信號為例,圖2所示為軸承分別在正常、內環故障、外環故障下的信號波形。由圖可知:正常信號幅值較小,幾乎無沖擊成分;內環故障信號信噪比差,由于受背景噪聲的影響,沖擊較不明顯,整個幅值范圍大于正常信號;外環故障情況相對正常信號幅值增大,沖擊更為明顯。通過時域信號幅值變化可以初步判斷信號正常與否,但無法確認故障類型。傳統的軸承故障診斷方法一般對信號進行解調分析,根據軸承零部件特征頻率分辨故障類型。對信號進行Hilbert包絡解調(500~1 500 Hz),結果如圖3所示。 圖3 解調譜Fig.3 Demodulation spectrum 由圖3可見,軸承信號在3類狀態下均出現輸入軸的轉頻fn,這可能是由于軸的制造誤差或者聯軸器存在輕微松動等因素造成,但轉頻成分幅值較小。后兩類信號中均出現故障成分對應的通過頻率fo,fi及其倍頻,據此可對故障所屬的類型進行判斷。但這種分析方法依賴于人的經驗,需選擇合適的頻段進行解調分析,診斷效率較低。 采用所提方法對每類振動信號進行時頻分析,分別作p=1,p=0.76的廣義S變換,獲得40幅時頻圖像,并與短時傅里葉分析進行對比。圖4為短時傅里葉變換結果(窗長為256),圖5和圖6為經標準S變換、廣義S變換(p=0.76)的時頻分布彩圖。由圖4可知,由于滑動的窗口大小固定,導致3類的時頻分辨性能固定,整體分辨性能低,特別是低頻信號成分無法得到良好的表達,內環故障、外環故障狀態高頻成分不明顯,使得內環故障狀態與正常狀態較難區分。由圖5可知,正常狀態信號在低頻處的聚焦性良好,故障狀態的頻率成分較為雜亂,在高頻成分的頻率分辨性過低,難以進行清晰的辨識和定位。整體來看,經標準S變換的軸承信號在低頻處的時頻分辨性較短時傅里葉分析結果有所提高。由圖6可知,正常狀態信號能量小,主要頻率分量集中在1 kHz附近,內環故障和外環故障情況在高頻處存在明顯的瞬時分量,且外環故障特征成分的整體能量大,其瞬時頻率表現出一定的規律性。對比圖4、圖5,廣義S變換能夠以較高時頻分辨率表示軸承振動中的非平穩特征,獲得的圖像具有良好的時頻聚焦特性,同時不同狀態的信號表現出一定的差異。 由于彩色數字圖像是由3個R,G,B矩陣分量組成,信息量大,給圖像的傳輸和存儲等帶來很大負擔。為了提高圖像傳輸和存儲效率,筆者利用加權平均法[18]將彩圖灰度化,得到軸承3種狀態下總共120幅灰度圖像,每幅圖像大小為900×1 200,含256個灰度等級。 2.3 特征提取的計算效率對比 由于生成的時頻圖像矩陣的維數巨大,當樣本數量大時特征提取效率將大大降低,因此,筆者將圖像劃分成90×120塊,每塊由10×10的矩陣組成,通過計算每塊所有元素之和來代表該塊的總能量值,這樣在保留時頻圖像矩陣能量分布的前提下大大降低了特征維數。為實現智能診斷,對每種狀態下取20組時頻圖像矩陣作為訓練樣本集,分別采用單向及雙向2DPCA算法、TD-2DLDA算法、2DNMF算法對時頻分布矩陣進行特征提取。后3種算法2次提取的特征維數分別為d和h,設置d=h取值為[2,3,…,10]。為進行對比分析,相應的單向2DPCA提取的特征維數設置為[4,9,16,…,100],這樣保證了不同方法特征提取維數的一致性。 表2給出了4種算法對經廣義S變換獲得的時頻圖像進行特征提取的計算效率,均不包含圖像載入時間。試驗環境為Matlab R2010b,Intel(R)1.73GHz,2.5 GB內存。由表2可得:隨著特征維數的增加,4種算法的計算時間相應增加;2DNMF的計算效率遠遠低于其余3種算法,這是因為二維非負矩陣在分解過程中需將所有訓練圖像矩陣按行或列進行拼合,拼合后的初始分解矩陣維數較大,而2DPCA及其雙向壓縮算法在計算過程中的總體散度矩陣始終保持原始圖像的維數;同時2DPCA特征提取的計算效率接近TD-2DLDA,略高于雙向2DPCA。 圖4 短時傅里葉變換Fig.4 Short time Fourier transfer result 圖5 標準S變換的時頻分布Fig.5 Time-frequency distribution based on standard S transform 圖6 廣義S變換(p=0.76)的時頻分布Fig.6 Time-frequency distribution based on generalized S transform 采用TD-2DPCA進行特征提取時,訓練結束后可得到最優投影矩陣P1 200×d和Q900×h,將原始樣本圖像矩陣向P和Q投影即可得到描述該樣本的特征參數。圖7為時頻圖像矩陣訓練集投影后對應的特征編碼矩陣,維數為10×10,圖中每行代表軸承的一類運行狀態,每種狀態只顯示前5個樣本。由特征圖可得,同類樣本各維度上特征編碼值的大小和分布相似,且反映該圖像的特征編碼值主要集中在左上角,其余編碼值均相對較小。這是因為每個圖像先進行一次橫向壓縮,提取的第一主成分位于第1列,再進行一次縱向壓縮,二次提取的前兩個主成分分別位于壓縮后的前兩行,集中體現了圖像的差異化信息。據此對比不同類樣本的特征圖可得,正常狀態的前兩個元素的編碼值均高于故障狀態,同時內環故障狀態特征圖第1列第2個元素與外環故障狀態所對應的元素編碼值差異較大。因此,TD-2DPCA算法能在壓縮圖像后保留圖像的差異信息,可以作為圖像特征提取的有效工具。 表2 不同算法提取特征的計算效率對比 Tab.2 Time cost of different algorithms s 特征維數特征提取算法2DNMFTD?2DPCATD?2DLDA2DPCA4(2×2)2.0000.2340.2340.2189(3×3)2.2770.2490.2370.22016(4×4)3.1530.2650.2490.23425(5×5)3.8300.2960.2500.25036(6×6)4.4600.3120.2650.25549(7×7)6.2200.3280.2660.26164(8×8)7.3300.3300.2730.26581(9×9)8.0200.3350.2810.266100(10×10)10.5410.3430.2910.286 2.4 軸承運行狀態分類 為對比4種方法提取的特征參數集的故障診斷性能,采用AMD距離分類器對軸承3類狀態進行區分。通過訓練獲取橫向與縱向的最優投影向量組,以此計算訓練樣本和測試樣本的特征編碼矩陣。對于某個測試樣本C,計算其至每個訓練樣本特征編碼矩陣的AMD距離,若與第i個訓練樣本的距離最小,則樣本C與第i個訓練樣本所屬的類別相同。診斷時,每種狀態40個樣本,隨機選擇20個樣本作為訓練集,剩余20個作為測試集。重復該過程10次,取測試結果的平均準確率作為分類性能評價指標。當提取的特征矩陣維數為10×10時,分析不同AMD距離參數q對診斷性能的影響,如圖8所示。對于標準S變換獲取的時頻圖像,隨著q的增大,分類準確率不斷增加。當q=1.2時達到最大,隨后趨于穩定。對于廣義S變換獲取的時頻圖像,參數q的取值對分類性能影響較小,準確率均保持在100%。 圖7 軸承時頻圖像特征編碼圖Fig.7 Feature code extracted from time-frequency image 圖8 AMD參數q對診斷性能的影響Fig.8 Impact of q on diagnosis performance 當AMD距離定義為Frobenius距離(即q=2)時,分析在不同特征維數下,2DPCA及其雙向壓縮算法、TD-2DLDA及2DNMF算法分別提取的特征子集的分類性能,如圖9所示。其中:圖9(a)的樣本圖像集來自廣義S變換(p=0.76);圖9(b)來自標準S變換。 圖9 不同特征提取方法分類性能對比Fig.9 Performance of the classifier based on different feature extraction schemes 由圖9(a)可知:在不同特征維數下,TD-2DLDA分類準確率相對較差,均低于80%;2DNMF算法的分類性能整體較優,但在提取特征維數為2×2,3×3時低于雙向2DPCA算法,其特征提取的計算效率也遠低于雙向2DPCA算法;2DPCA及其雙向壓縮方法所提取特征子集的分類準確率差別不大,均保持在95%以上,且當提取特征維數較少時,雙向2DPCA算法的分類性能優于其余3種方法。由圖9(b)可知:經廣義S變換后,TD-2DLDA算法的分類準確率較標準S變換有了明顯的提高,但仍低于其余3類算法;2DNMF算法具有較高的分類準確性,但當提取的特征維數較高時反而略有下降;除了2DNMF算法外,其余特征提取方法的診斷性能較標準S變換均有所提升,這是由于分類的圖像集具有良好的時頻聚焦特性,各類狀態差異性相對更為明顯;對于2DPCA及其雙向壓縮算法,特征維數的選擇對診斷性能的影響并不明顯。對軸承3類狀態的診斷結果表明,雙向2DPCA算法在提取特征維數較低時仍具有良好的識別準確率,基于廣義S變換時頻圖像的診斷性能較標準S變換高。 1) 廣義S變換較標準S變換有更好的時頻聚焦特性,能夠反映故障狀態下軸承信號的時頻分布特點,因此廣義S變換可用于軸承故障狀態的區分,同時將其與2DPCA算法結合,能有效地提取軸承運行狀態的差異特征。 2) 傳統的故障診斷方法基于一維信號,診斷效率較低,將雙向2DPCA算法成功應用于軸承故障信息的特征提取。試驗表明,雙向2DPCA算法在保證分類性能的前提下,計算效率遠遠高于2DNMF。在采用雙向2DPCA算法對時頻圖像進行特征提取時,應當選擇合適的特征維數來兼顧計算效率和分類準確率。 [1] 楊宇,何怡剛, 程軍圣,等.用最大重疊離散小波包變換的Hilbert譜時頻分析[J].振動、測試與診斷,2009,29(1):10-13. Yang Yu, He Yigang, Cheng Junsheng, et al. Time-frequency analysis of hilbert spectrum based on maximal overlap discrete wavelet packet transform[J]. Journal of Vibration, Measurement & Diagnosis, 2009,29(1):10-13.(in Chinese) [2] 趙鳳展,楊仁剛.基于短時傅里葉變換的電壓暫降擾動檢測[J].中國電機工程學報,2007,27(10):28-34,109. Zhao Fengzhan,Yang Rengang.Voltage sag disturbance detection based on short time fourier transform[J]. Proceedings of the Chinese Society for Electrical Engineering, 2007,27(10):28-34,109.(in Chinese) [3] Stockwell R G, Mansinha L ,Lowe R P. Localization of the complex spectrum:the S-transform[J]. IEEE Transactions on Signal Processing,1996,17:998-1001. [4] 翟俊海,趙文秀,王熙照,等.圖像特征提取研究[J].河北大學學報,2009,29(1):106-112. Zhai Junhai, Zhao Wenxiu, Wang Xizhao, et al. Research on the image feature extraction[J]. Journal of Hebei University,2009,29(1):106-112.(in Chinese) [5] Yang Jian, Zhang D, Yang Jingyu. Two-dimensional PCA: a new approach to appearance-based face representation and recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2004, 26(1):131-137. [6] Li Ming, Yuan Baozong. 2D-LDA: a statistical linear discriminant analysis for image matrix[J].Pattern Recognition Letters,2005,26(5):527-532. [7] 陳伏兵,陳秀宏,高秀梅,等.二維主成分分析方法的推廣及其在人臉識別中的應用[J].計算機應用,2005,25(8):1767-1770. Chen Fubing, Chen Xiuhong, Gao Xiumei, et al. Generalization of 2DPCA and its application in face recognition[J]. Journal of Computer Applications, 2005,25(8):1767-1770.(in Chinese) [8] Li Bing, Zhang Peilin, Liu Dongsheng, et al. Classification of time-frequency representations based on two-direction 2DLDA for gear fault diagnosis[J]. Applied Soft Computing, 2011,11(8): 5299-5305. [9] 李宏坤,陳禹臻,張志新,等.基于非負矩陣分解與主元分析的時頻圖像識別方法研究[J].振動與沖擊,2012(18):169-172. LI Hongkun, Chen Yuzhen, Zhang Zhixin, et al. Time-frequency image identification using non-negative matrix factorization and principal component analysis[J]. Journal of Vibration and Shock,2012(18):169-172.(in Chinese) [10]Li Bing, Zhang Peilin, Tian Hao, et al. A new feature extraction and selection scheme for hybrid fault diagnosis of gearbox[J]. Expert Systems with Applications, 2011,38(8): 10000-10009. [11]李兵,米雙山,劉鵬遠,等.二維非負矩陣分解在齒輪故障診斷中的應用[J].振動、測試與診斷,2012,32(5):836-840. Li Bing, Mi Shuangshan, Liu Pengyuan,et al. Application of two-dimensional non-negative factorization for gear fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(5): 836-840.(in Chinese) [13]Stankovi L. A measure of some time-frequency distributions concentration[J]. Signal Processing, 2001, 81(3): 621-631. [14]Li Bing, Zhang Peilin, Liu Dongsheng, et al. Feature extraction for rolling element bearing fault diagnosis utilizing generalized S-transform and two-dimensional non-negative matrix factorization[J].Journal of Sound and Vibration, 2011, 330(10): 2388-2399. [15]Jian Yang, Zhang D, Frangi A F, et al. Two-dimensional PCA: a new approach to appearance- based face representation and recognition[J].Pattern Analysis and Machine Intelligence,2004,26(1):131-137. [16]Vytautas P. Distance measures for PCA-based face recognition[J]. Pattern Recognition Letters,2004,25(6): 711-724. [17]Zuo Wangmeng, Zhang D, Wang Kuanquan. An assembled matrix distance metric for 2DPCA-based image recognition[J]. Pattern Recognition Letters, 2006,27(3): 210-216. [18] 夏良正.數字圖像處理[M].南京:東南大學出版社,1999:20-22. 10.16450/j.cnki.issn.1004-6801.2015.03.016 *國家自然科學基金資助項目(51075150,51475170) 2013-12-19; 2014-02-24 TP751; TH113 李巍華,男,1973年11月生,博士、教授。主要研究方向為車輛性能測試、NVH振動信號分析、模式識別。曾發表《基于改進證據理論及多神經網絡融合的故障分類》(《機械工程學報》2010年第46卷第9期)等論文。 E-mail:whlee@scut.edu.cn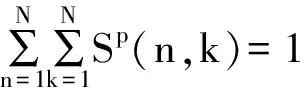

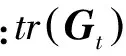
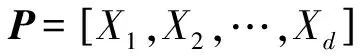

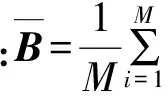
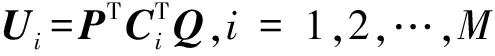
2 試驗驗證







3 結 論


