基于三次B樣條曲線的食品物性檢測(cè)系統(tǒng)的仿生咀嚼運(yùn)動(dòng)軌跡規(guī)劃

□ 馬德軍 □ 王加森 □ 盧 慧 □ 俞經(jīng)虎,2

1.江南大學(xué) 機(jī)械工程學(xué)院 江蘇無(wú)錫 214122

2.江蘇省食品先進(jìn)制造裝備技術(shù)重點(diǎn)實(shí)驗(yàn)室 江蘇無(wú)錫 214122

隨著食品行業(yè)的工業(yè)化和標(biāo)準(zhǔn)化發(fā)展，目前，市場(chǎng)已有的食品物性檢測(cè)質(zhì)構(gòu)儀［1］多為功能單一的專用儀器，而且測(cè)試運(yùn)動(dòng)也為簡(jiǎn)單的上下直線運(yùn)動(dòng)，而物性檢測(cè)的最終標(biāo)準(zhǔn)是人的口腔咀嚼感覺(jué)，本文研究的基于6-UPS并聯(lián)機(jī)器人［2］食品物性檢測(cè)裝置，通過(guò)模仿人的咀嚼運(yùn)動(dòng)來(lái)實(shí)現(xiàn)對(duì)食品物性參數(shù)的檢測(cè)，從原理上有助于提高食品物性的檢測(cè)準(zhǔn)確性 。

以仿生學(xué)為基礎(chǔ)，根據(jù)正常人下頜咀嚼運(yùn)動(dòng)的運(yùn)動(dòng)軌跡掃描研究的結(jié)果，對(duì)仿生咀嚼運(yùn)動(dòng)空間軌跡進(jìn)行構(gòu)建，然后利用運(yùn)動(dòng)學(xué)逆解將笛卡爾空間運(yùn)動(dòng)軌跡轉(zhuǎn)換為連桿空間運(yùn)動(dòng)，最終利用三次B樣條函數(shù)在連桿空間路徑點(diǎn)之間進(jìn)行插值運(yùn)算，構(gòu)造出仿生咀嚼運(yùn)動(dòng)的連桿運(yùn)動(dòng)軌跡函數(shù)，并運(yùn)用實(shí)例驗(yàn)證軌跡規(guī)劃效果。

1 6-UPS并聯(lián)機(jī)器人結(jié)構(gòu)參數(shù)設(shè)置及坐標(biāo)建立

▲圖1 6-UPS并聯(lián)機(jī)構(gòu)的結(jié)構(gòu)簡(jiǎn)圖及俯視圖

6-UPS并聯(lián)機(jī)構(gòu)初始位置時(shí)的結(jié)構(gòu)簡(jiǎn)圖及俯視圖如圖1所示，上平臺(tái)和下平臺(tái)的中心點(diǎn)在水平投影面上相重合。圖中標(biāo)注了下平臺(tái)的下鉸點(diǎn)Ui（i=1，2，...，6），Ui繞圓周依次排列形成不等邊對(duì)稱六邊形，其中U1U3U5、U2U4U6分別形成等邊三角形，外接在半徑為R的圓上，短邊U1U2所對(duì)應(yīng)的圓心角為α1；上平臺(tái)上鉸點(diǎn)在圖中表示為 Si（i=1，2，...，6），Si也形成一個(gè)不等邊對(duì)稱六邊形，其中S1S3S5、S2S4S6分別構(gòu)成等邊三角形，z外接在半徑為r的圓上，長(zhǎng)邊S1S2所對(duì)應(yīng)的圓心角為α2。

▲圖2 26～30歲的正常人群咀嚼運(yùn)動(dòng)軌跡在冠狀面、矢狀面和水平面的投影

為了便于分析與計(jì)算，建立如圖1所示坐標(biāo)系。在并聯(lián)機(jī)構(gòu)下平臺(tái)上建立全局坐標(biāo)系O1-XYZ，坐標(biāo)原點(diǎn)O1是下平臺(tái)的幾何中心點(diǎn)，軸線X垂直于短邊U1U2，軸線Z經(jīng)過(guò)上下平臺(tái)的幾何中心點(diǎn)向上，軸線X、Y、Z方向滿足右手定則；建立靜坐標(biāo)系O-xyz，固結(jié)于上頜骨，靜坐標(biāo)系原點(diǎn)O是左右髁突鉸鏈軸的中心點(diǎn)，軸線 x、y、z與全局坐標(biāo)系｛O1｝的 X、Y、Z 平行；動(dòng)坐標(biāo)系P-uvw固結(jié)于下頜骨上，坐標(biāo)原點(diǎn)P為下頜切點(diǎn)，軸線u、v、w方向滿足右手定則，如圖1所示，初始位置與全局坐標(biāo)系的X、Y、Z平行。

2 仿生咀嚼運(yùn)動(dòng)空間軌跡構(gòu)建

昆明醫(yī)科大學(xué)的李娟［3］采用SAM下頜運(yùn)動(dòng)軌跡掃描記錄儀檢測(cè)了不同年齡組正常人群咀嚼運(yùn)動(dòng)的軌跡及幅度，根據(jù)正常人群咀嚼運(yùn)動(dòng)軌跡的測(cè)試結(jié)果，繪出了26～30歲的人群冠狀面、矢狀面和水平面的咀嚼運(yùn)動(dòng)軌跡的咀嚼運(yùn)動(dòng)圖，如圖2所示。

從圖2的總體看，人的咀嚼運(yùn)動(dòng)軌跡是復(fù)雜的，但從單張圖可以發(fā)現(xiàn)，在冠狀面中咀嚼運(yùn)動(dòng)軌跡近似為一個(gè)傾斜的橢圓，而反映人在咀嚼運(yùn)動(dòng)時(shí)，張口和閉口的運(yùn)動(dòng)軌跡在矢狀面內(nèi)的軌跡基本相重合，咀嚼運(yùn)動(dòng)軌跡在水平面內(nèi)的掃描軌跡也近似于一個(gè)傾斜的橢圓。根據(jù)以上分析結(jié)果，可以認(rèn)為正常人咀嚼運(yùn)動(dòng)的笛卡爾空間軌跡形狀與空間橢圓相近似。為了實(shí)現(xiàn)基于6－UPS并聯(lián)機(jī)器人的食品物性仿生檢測(cè)平臺(tái)良好的運(yùn)動(dòng)仿生特性，決定將咀嚼運(yùn)動(dòng)的軌跡等效為空間橢圓軌跡，該空間橢圓軌跡可以由平面橢圓通過(guò)幾個(gè)空間的位姿變換最終確定，橢圓上的點(diǎn)（即動(dòng)坐標(biāo)系原點(diǎn)）在靜坐標(biāo)系中的位置為：式 中 ：sφT為 sinφT；cφT為cosφT；a、b 分別為橢圓軌跡的長(zhǎng)半軸和短半軸；φT、θT分別為橢圓長(zhǎng)軸在與初始動(dòng)坐標(biāo)系位姿相同的固定坐標(biāo)系的xoz平面和yoz平面內(nèi)的投影與z軸負(fù)方向的夾角；α11為橢圓運(yùn)動(dòng)角度；h為上下平臺(tái)間的垂直距離；h1為動(dòng)坐標(biāo)系原點(diǎn)P距上平臺(tái)的垂直距離；h2為靜坐標(biāo)系原點(diǎn)O距下平臺(tái)的垂直距離。

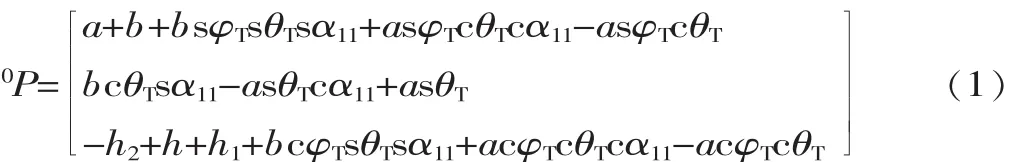
以上為動(dòng)坐標(biāo)系原點(diǎn)P在α11處的位置，要求出動(dòng)坐標(biāo)系原點(diǎn)P在靜坐標(biāo)系｛O｝中的位姿還需要求動(dòng)坐標(biāo)系在α11處的姿態(tài)變化。

根據(jù)咀嚼運(yùn)動(dòng)的實(shí)際情況可知，人的下頜骨在運(yùn)動(dòng)的過(guò)程中，姿態(tài)的變化可分解為繞靜坐標(biāo)系的y軸旋轉(zhuǎn)的張口運(yùn)動(dòng)和繞靜坐標(biāo)系的z軸旋轉(zhuǎn)的左右擺動(dòng)。當(dāng)動(dòng)坐標(biāo)系原點(diǎn)運(yùn)動(dòng)到某一位置時(shí)，這兩個(gè)角度可由動(dòng)坐標(biāo)系原點(diǎn)P與靜坐標(biāo)系原點(diǎn)O的連線的向量OP分別在xoz和xoy平面上與x軸正方向的夾角表示。

設(shè)向量OP在xoz平面上與x軸正方向的夾角為φ1，即動(dòng)坐標(biāo)系繞靜坐標(biāo)系的y軸旋轉(zhuǎn)角度。向量OP在xoy平面上與x軸正方向的夾角為φ2，即動(dòng)坐標(biāo)系繞靜坐標(biāo)系的z軸的旋轉(zhuǎn)角度。由下式可求得：

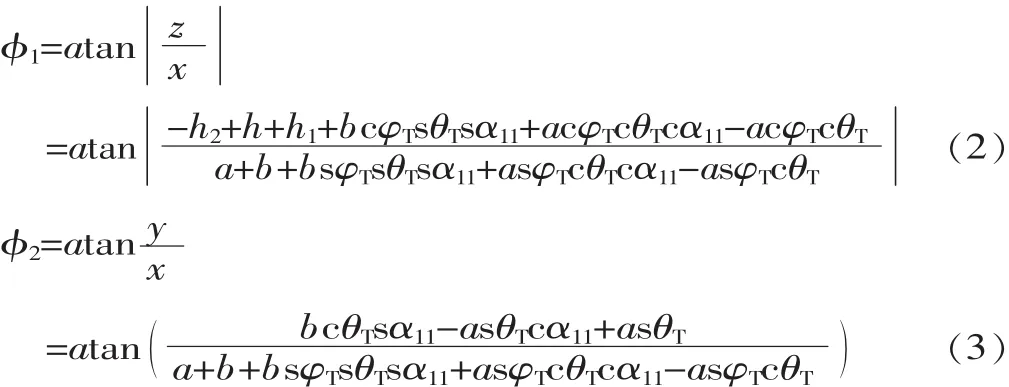
至此，在空間運(yùn)動(dòng)軌跡中某一時(shí)刻，動(dòng)坐標(biāo)系的位姿參數(shù)全部確定。

3 基于三次B樣條的仿生咀嚼運(yùn)動(dòng)連桿空間軌跡規(guī)劃

連桿空間用三次B樣條曲線進(jìn)行軌跡規(guī)劃就是通過(guò)B樣條函數(shù)的反算方法得到各連桿變量l關(guān)于時(shí)間t的函數(shù)表達(dá)式［4］，反算就是利用給定的B樣條曲線上的部分已知路徑點(diǎn)，來(lái)求解B樣條曲線的控制點(diǎn)（特征多邊形頂點(diǎn)），進(jìn)而構(gòu)造曲線的函數(shù)表達(dá)式。

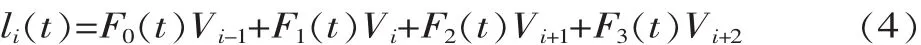
設(shè)某段時(shí)間內(nèi)三次B樣條曲線的函數(shù)式為:式中：t為時(shí)間（0≤t≤1）；F（t）為時(shí)間變量的多項(xiàng)式，即三次 B 樣條的基函數(shù)； Vi-1、Vi、Vi+1、Vi+2為該段三次B樣條曲線的控制點(diǎn)。

根據(jù)連桿軌跡的連續(xù)性、連桿軌跡導(dǎo)數(shù)的連續(xù)性、B樣條基函數(shù)的規(guī)范性條件推導(dǎo)可得：

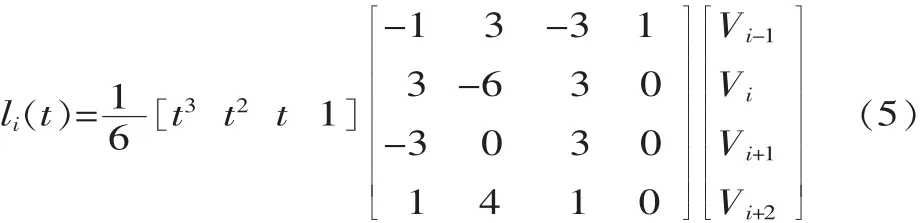
由式（5）可知，要計(jì)算B樣條函數(shù)的表達(dá)式首先需要求出一系列控制點(diǎn)Vi。由于假設(shè)并聯(lián)機(jī)器人各連桿路徑點(diǎn)為已知，所以不妨假設(shè)某連桿的軌跡有m-1段三次 B 樣條曲線組成，路徑點(diǎn)為 pi（i=1，2，...，m），由軌跡連續(xù)性可得:

根據(jù)模擬咀嚼運(yùn)動(dòng)的實(shí)際情況，各連桿運(yùn)動(dòng)軌跡在初始點(diǎn)和終止點(diǎn)的速度需為零，以此作為邊界約束條件［5］，可得：

將式（6）和式（7）聯(lián)立寫成矩陣形式為：

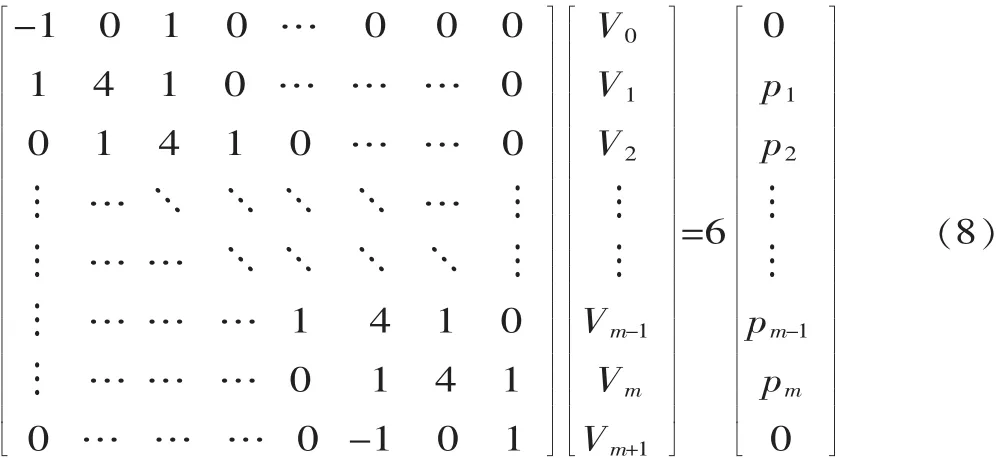
由式（8）可以看出，該線性方程組共有m+2個(gè)未知數(shù)，同時(shí)有m+2個(gè)方程，故可以確定唯一解V0、V1、...、Vm、Vm+1。

這樣，根據(jù)已知路徑點(diǎn)即可得到B樣條曲線的所有控制點(diǎn)，機(jī)器人各連桿的整個(gè)運(yùn)動(dòng)軌跡可由m-1個(gè)三次B樣條函數(shù)分段表示，進(jìn)而可得到整個(gè)連桿軌跡的表達(dá)式。

4 仿生咀嚼運(yùn)動(dòng)軌跡規(guī)劃實(shí)例

根據(jù)設(shè)計(jì)的仿生咀嚼平臺(tái)的尺寸及作咀嚼運(yùn)動(dòng)的軌跡運(yùn)動(dòng)范圍的大小，分別取各參數(shù)如下。

初始位置時(shí)，取上下平臺(tái)間的垂直距離h=200 mm，上平臺(tái)外接圓半徑r=50 mm，下平臺(tái)外接圓半徑R=100 mm，動(dòng)坐標(biāo)系原點(diǎn)P距上平臺(tái)的垂直距離h1=50 mm，距全局坐標(biāo)系原點(diǎn)O1的水平正向距離a1=50 mm，靜坐標(biāo)系原點(diǎn)O距下平臺(tái)的垂直距離h2=（h+h1+20）mm，距全局坐標(biāo)系原點(diǎn)O1的水平負(fù)向距離b1=50 mm。

而對(duì)于空間橢圓軌跡，取橢圓的長(zhǎng)半軸a=50 mm，短半軸 b=30 mm，φT=atan（1/2），θT=π/12。 設(shè)動(dòng)坐標(biāo)系沿橢圓軌跡運(yùn)動(dòng)一周所用的周期T1=4 s，則運(yùn)動(dòng)的角速度ω=π/2（rad/s）。軌跡規(guī)劃時(shí)將橢圓軌跡均等分成n=8份，則對(duì)應(yīng)節(jié)點(diǎn)的橢圓運(yùn)動(dòng)角度α11=ωt，其中t為對(duì)應(yīng)節(jié)點(diǎn)的時(shí)刻。此外，上平臺(tái)鉸點(diǎn)構(gòu)成的六邊形的長(zhǎng)邊所對(duì)應(yīng)的外接圓圓心角α2=5π/12，下平臺(tái)鉸點(diǎn)構(gòu)成的六邊形的短邊所對(duì)應(yīng)的外接圓圓心角α1=π/4。將橢圓運(yùn)動(dòng)軌跡等分成n=8份，根據(jù)參量的設(shè)置，即α11=（π/4）i（i=0，1，...，8）。

由動(dòng)坐標(biāo)系的位置時(shí)間式（1）及動(dòng)坐標(biāo)系姿態(tài)時(shí)間式（2）和式（3），將參數(shù)值代入后，可分別求出9個(gè)節(jié)點(diǎn)處動(dòng)坐標(biāo)系在靜坐標(biāo)系的位置和姿態(tài)。將求得的笛卡爾空間橢圓軌跡上的9個(gè)節(jié)點(diǎn)處動(dòng)坐標(biāo)系在靜坐標(biāo)系的位置和姿態(tài)值代入逆運(yùn)動(dòng)學(xué)推導(dǎo)獲得的公式，即可求出時(shí)刻上鉸點(diǎn) Si（i=1，2，...，6）在坐標(biāo)系｛O｝中的坐標(biāo)值和對(duì)應(yīng)節(jié)點(diǎn)處連桿的桿長(zhǎng)。

至此，完成了由笛卡爾空間橢圓軌跡上的點(diǎn)到連桿坐標(biāo)系桿長(zhǎng)的求解。根據(jù)以上參數(shù)求解的節(jié)點(diǎn)桿長(zhǎng)結(jié)果，代入三次B樣條曲線控制節(jié)點(diǎn)求解式（8），求得三次B樣條曲線的控制節(jié)點(diǎn)V的結(jié)果。

以上方程為三次B樣條曲線的求解公式，推導(dǎo)出6根連桿的三次B樣條曲線插值方程。

綜上可以看出，將橢圓軌跡按周期等分成8段，由根據(jù)路徑點(diǎn)求解出構(gòu)建3次B樣條曲線函數(shù)所需要的10個(gè)控制節(jié)點(diǎn)對(duì)每段進(jìn)行插值，最終可以看到機(jī)器人各連桿的整個(gè)運(yùn)動(dòng)軌跡可由8個(gè)三次B樣條函數(shù)分段表示，進(jìn)而可得到整個(gè)連桿軌跡的表達(dá)式。

對(duì)應(yīng)以上獲得的6根連桿三次B樣條曲線軌跡規(guī)劃方程，軌跡的桿長(zhǎng)l、速度v、加速度a變化曲線分別如圖3所示。

從軌跡規(guī)劃方程的桿長(zhǎng)變化曲線圖和速度變化曲線圖可以看出，6根連桿的桿長(zhǎng)變化和伸縮速度變化平滑且連續(xù)，而且軌跡規(guī)劃獲得的方程能夠很好地滿足初速度和結(jié)束速度為零的要求。說(shuō)明上述利用三次B樣條曲線進(jìn)行連桿軌跡規(guī)劃的推導(dǎo)過(guò)程完全合理正確。

5 結(jié)束語(yǔ)

筆者以實(shí)現(xiàn)食品物性檢測(cè)系統(tǒng)檢測(cè)運(yùn)動(dòng)的仿生咀嚼運(yùn)動(dòng)為目標(biāo)，通過(guò)對(duì)人下頜咀嚼運(yùn)動(dòng)軌跡進(jìn)行分析，建立了檢測(cè)運(yùn)動(dòng)的空間仿生咀嚼運(yùn)動(dòng)軌跡，運(yùn)用運(yùn)動(dòng)學(xué)反解和三次B樣條曲線，構(gòu)建出了便于實(shí)現(xiàn)控制的連桿運(yùn)動(dòng)軌跡方程，為食品物性檢測(cè)系統(tǒng)的研究提供了良好的理論基礎(chǔ)和設(shè)計(jì)思路。

▲圖3 6根連桿軌跡規(guī)劃方程的桿長(zhǎng)、速度、加速度變化曲線圖

［1］ 胡亞云．質(zhì)構(gòu)儀在食品研究中的應(yīng)用現(xiàn)狀［J］．食品研究與開(kāi)發(fā)，2013，34（11）:101－104．

［2］ 吳培棟．Stewart平臺(tái)的運(yùn)動(dòng)學(xué)與逆動(dòng)力學(xué)的基礎(chǔ)研究［D］．武漢:華中科技大學(xué)，2008．

［3］ 李娟．不同年齡組正常人群的下頜運(yùn)動(dòng)軌跡及咀嚼肌表面肌電比較研究［D］．昆明:昆明醫(yī)科大學(xué)，2013．

［4］ 牛永康．六自由度串聯(lián)機(jī)器人軌跡規(guī)劃時(shí)間最優(yōu)研究［D］．長(zhǎng)春:長(zhǎng)春工業(yè)大學(xué)，2013．

［5］ 張洪強(qiáng)．工業(yè)機(jī)器人時(shí)間最優(yōu)軌跡規(guī)劃［D］．長(zhǎng)沙:湖南大學(xué)，2004．