圓柱正弦活齒傳動機構傳動比和傳動條件研究*
□ 曾運運 □ 袁新梅 □ 周思柱
長江大學機械結構強度與振動研究所 湖北 荊州 434000
活齒傳動分為平面活齒傳動和空間活齒傳動,目前為止,活齒傳動研究主要集中在平面活齒,而空間活齒傳動研究得比較少,但現在已經有學者開始將平面活齒傳動理論和空間活齒傳動理論聯系起來進行研究。文獻[1]分析了圓柱面空間活齒傳動和平面活齒傳動,指出可以將圓柱面活齒傳動轉化為平面活齒傳動來分析。圓柱正弦活齒傳動屬于圓柱面空間活齒傳動,筆者采用展開法,將圓柱正弦活齒傳動轉化為平面活齒傳動,推導出該傳動的傳動比公式和連續傳動條件,并進行實例計算,驗證上述結論。
1 傳動比計算
圓柱正弦活齒傳動主要由主動軸、殼體、導架及活齒4個部分組成,主動軸外表面有外正弦滾道,周期數為Z1,活齒架上均勻分布著軸向活齒槽,殼體內表面有內正弦滾道,周期數為Z3,在外、內滾道及活齒槽交錯區域內安裝球形活齒。
為了便于分析,將殼體固定,以主動軸為輸入軸,活齒架為輸出軸,推導傳動比公式。轉角φ0和角速度ω之間的關系為ω=因此,主動軸和活齒架之間的傳動比可以用轉角來表示。該傳動機構在工作過程中,活齒沿外正弦滾道作相對運動,沿內正弦滾道作絕對運動,圖1為活齒沿外、內正弦滾道運動平面的展開圖,線1和線2分別代表外、內正弦滾道的正弦軌跡,θ0代表活齒初始位置。線3代表線1在主動軸旋轉Δθ后的曲線,線1、2、3的方程如下:


▲圖1 活齒軌跡平面展開圖
當活齒在初始位置 θ0時,聯立式(1)和式(2)可得:
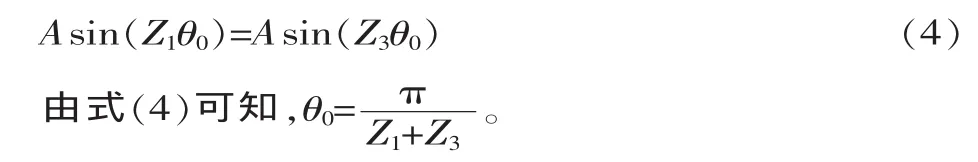
若主動軸和活齒架同向運動,當主動軸轉過角度為Δθ1、活齒由初始位置θ0轉到θ1時,其轉過角度為Δθ2,聯立式(2)和式(3)可得:

若主動軸和活齒架反向運動,當主動軸轉過角度為Δθ1,活齒由初始位置θ0轉到θ2時,其轉過角度為Δθ2。 聯立式(2)和式(3)可得:
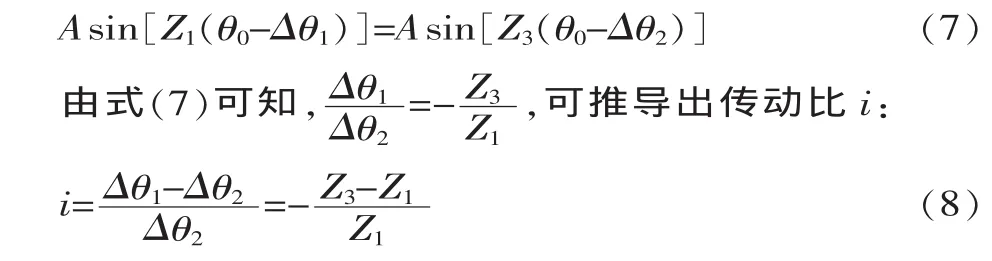
2 連續傳動條件
連續運動條件是圓柱正弦活齒傳動機構正常工作所必須滿足的條件之一[2]。圓柱正弦活齒傳動機構連續傳動條件為:在工作中至少有一個活齒處于嚙合狀態,并且所有活齒均可連續接觸正弦滾道齒面。
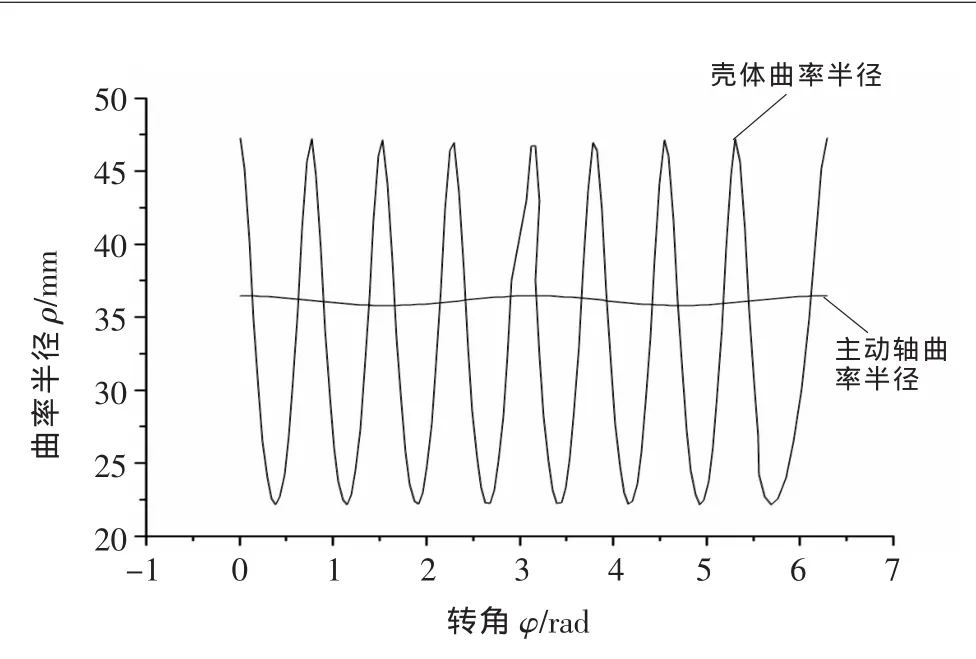
現以活齒在主動軸外正弦滾道運動為例,將主動軸外圓表面沿直母線展開。由外正弦滾道形狀得知,當活齒嚙合區域的小圓半徑ra小于主動軸外正弦滾道理論齒廓曲線L的最小曲率半徑ρmin,即ρmin>ra時,則不會發生頂切;當ρmin 式中:r1為主動軸半徑;φ為活齒中心在圓周方向的位置角;A為正弦幅值。 曲線L上任意一點的位置矢量r=xi+yj+zk,根據微分幾何[3]可知曲率 ρ: 將式(9)代入式(10)中,求解得到主動軸最小曲率半徑為: 當ρmin>ra時,主動軸的外正弦滾道理論齒廓曲線不會發生頂切。根據活齒結構的幾何關系有ra= 式中:b1為主動軸的正弦滾道深度;r0為活齒半徑。 同理,可得殼體正弦滾道理論齒廓曲線最小曲率半徑為: 從而得出殼體正弦滾道理論齒廓曲線不發生頂切的條件為: 式中:b3為殼體的正弦滾道深度;r3為殼體的內圓柱面半徑。 已知圓柱正弦活齒傳動機構的初始參數為Z1=1、Z3=4、A=4mm及主動軸和活齒架同向轉動,利用式(6)可知,圓柱正弦活齒傳動機構的傳動比i=5。 為保證滾道齒面不發生頂切,要求各結構參數滿足式(12)、式(14),以此來確定該傳動機構的結構參數,見表1。 表1 圓柱正弦活齒傳動結構參數 ▲圖2 主動軸曲率半徑變化曲線 利用式(11)、式(13)可以算出主動軸滾道理論正弦齒廓曲線最小曲率半徑ρmin=35.78mm和殼體滾道理論正弦齒廓曲線最小曲率半徑ρmin=22.12mm,利用Pro/E曲率分析功能,對主動軸和殼體理論正弦齒廓曲線進行分析,繪制曲率半徑隨相對角度變化的曲線,如圖2所示。通過分析發現,由Pro/E計算的主動軸和殼體的最小曲率半徑與由式(11)、式(13)算出的主動軸滾道和殼體滾道的理論正弦齒廓曲線最小曲率半徑完全吻合,可以證明式(11)、式(13)完全正確。將上述結構參數代入 ra=中,可求出ra=3.69mm,最小曲率半徑遠遠大于ra,所以,活齒可以在主動軸和殼體的正弦滾道中連續運動,不會發生頂切。 (1)圓柱正弦活齒傳動機構的傳動比主要由主動軸正弦滾道周期數Z1、殼體正弦滾道周期數Z3和主動軸與活齒架轉向決定。 (2) 所選結構參數必須滿足式(12)、式(14),才能保證圓柱正弦活齒傳動機構能夠連續運動。 [1] 黃勁枝,陳賢湘,程時甘.雙余弦活齒傳動嚙合曲線的研究[J].機械傳動,2008(4):6-7. [2] 曲繼方.活齒傳動理論[M].北京:機械工業出版社,1993. [3] 傅則紹.微分幾何與齒輪嚙合原理[M].青島:石油大學出版社,1999.




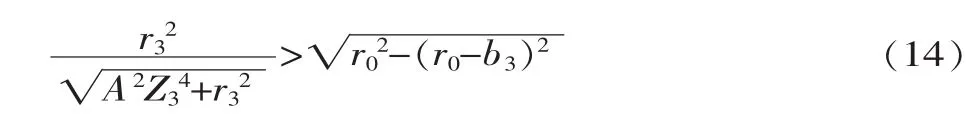
3 計算實例

4 結論

