四旋翼無人機模糊自抗擾姿態控制及穩定性分析

竇景欣，孔祥希，聞邦椿

（東北大學 機械工程及自動化學院，沈陽 110819）

四旋翼無人機模糊自抗擾姿態控制及穩定性分析

竇景欣，孔祥希，聞邦椿

（東北大學 機械工程及自動化學院，沈陽 110819）

針對四旋翼無人機姿態控制問題，設計了一種基于模糊自抗擾控制的四旋翼姿態控制器。分析了四旋翼無人機的動力學模型，給出了基于模糊自抗擾控制算法的姿態控制方案，并設計了對應的模糊自抗擾控制算法的擴張狀態觀測器和模糊狀態誤差反饋控制器。通過穩定性分析，得出了擴張狀態觀測器估計誤差是有界的，同時給出了反饋誤差穩定的充分條件。仿真結果表明，所設計的模糊自抗擾控制器，同經典自抗擾控制器相比，系統平均超調量減小約75%，降低了擾動造成的輸出波動幅值約30%，表明該控制系統提高了系統穩定性和對干擾抑制能力，滿足對四旋翼姿態控制要求。

四旋翼無人機；姿態控制；擴張狀態觀測器；自抗擾控制；模糊控制

四旋翼無人機的控制器設計主要包括線性和非線性設計兩類。線性設計包括線性二次型控制[1]、PID控制[2]等，這些控制方法在四旋翼無人機上得到了應用，并且能保證在設定的平衡點的飛行性能，但是在遇到干擾或偏離平衡點時，飛行性能就會急速降低。

為了獲得高性能的控制效果，非線性方法得到廣泛的研究。例如在文獻[3]中設計一種反步控制器，用于四旋翼的姿態控制。其他非線性方法應用于四旋翼無人機的控制還有自適應控制[4-5]、神經網絡控制[6-8]、魯棒控制[9]、非線性控制[10]等。除了應用非線性方法，在設計控制方法時也考慮了模型中的未建模部分和外擾等因素的影響。文獻[11]設計了一種自適應非線性控制器，用于控制考慮時變質量的四旋翼飛行器。文獻[12]設計了一種混合模糊和反步滑模控制器，用于克服四旋翼模型的不確定性和未知外擾。文獻[13]在考慮四旋翼模型不確定性情況下，設計了帶有魯棒補償器的PD控制器。Islam等人[14]在文獻中假定模型全參數已知前提下，設計了一種自適應滑模控制器，并逐一驗證了在四旋翼飛行器遭遇風場、變質量等擾動情況下控制器的魯棒性。何勇靈等人在文獻[15]中考慮四旋翼在風場干擾的條件下，設計了基于積分反演算法的內環姿態控制和基于 PID的外環控制組成的控制器，并驗證了控制器在紊流風場干擾下控制性能良好并具有較強的魯棒性。

上述文獻中提及的非線性方法存在如下的不足之處。首先是這些方法在控制器設計過程中，對系統模型的精度要求較高，或者是需要獲得四旋翼無人機模型的全狀態反饋。但是在實際應用中，上述要求幾乎是不能實現的。

自抗擾控制算法[16]是我國學者韓京清提出的一種不依賴于系統模型的控制算法，其核心思想是應用擴張狀態觀測器進行干擾的估計、補償，實現系統的動態反饋線性化。同時該算法具有超調小、響應快速、高精度控制及適于數字化實現等特點，引起國內外學者廣泛的深入研究和應用[17-18]。但是由于ADRC中狀態誤差反饋律的自適應性較差，降低了整個算法的性能。為此，本文設計了基于模糊線性自抗擾控制器的四旋翼無人機姿態控制系統，將模糊控制引入自抗擾控制器中狀態誤差反饋律中進行參數自整定，提高了系統的自適應性和魯棒性。

1 四旋翼無人機動力學建模

由圖1可知，四旋翼無人機通過調整四個旋翼的轉速，進行六個自由度的運動，是一個典型的欠驅動模型。

設定機體坐標系為 B(oxyz)，地面坐標系為E(OXYZ)。視四旋翼無人機做剛體運動，飛行器的質心和機體坐標原點坐標重合，考慮在姿態變化不大的情況下進行控制。基于以上設定條件，采用牛頓–歐拉法建立四旋翼無人機動力學模型[4,7]。

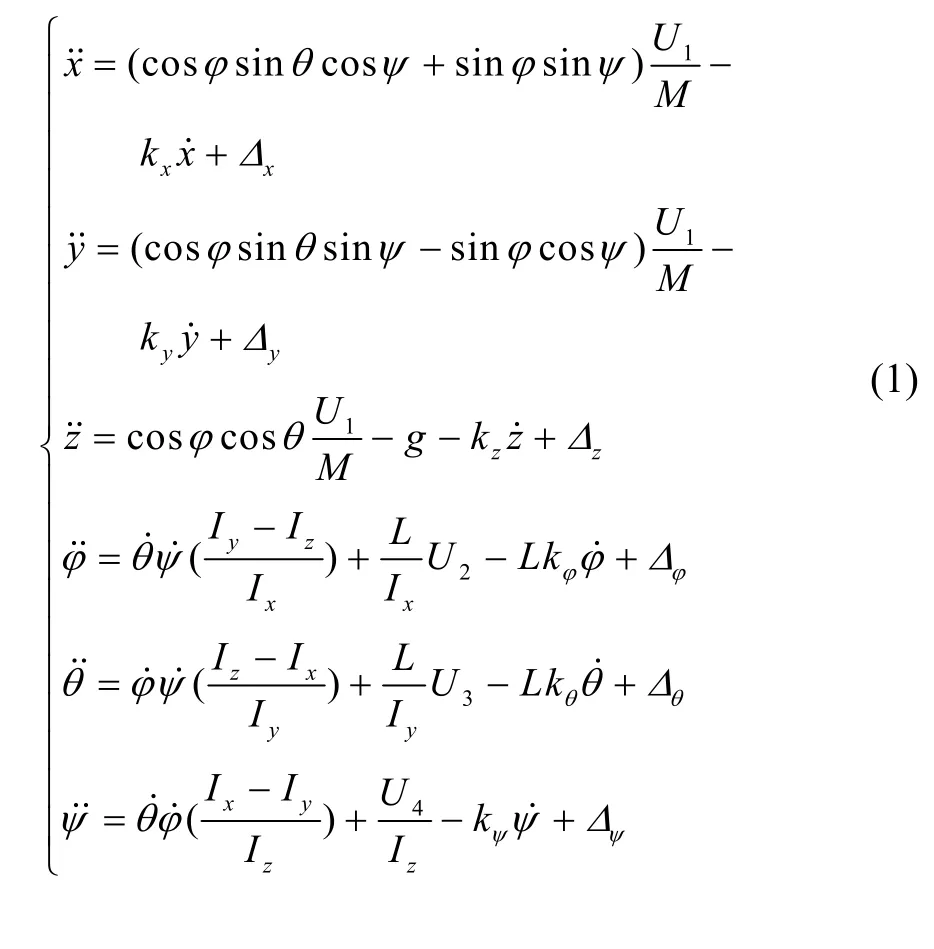
式中，U1～U4及Ω分別為

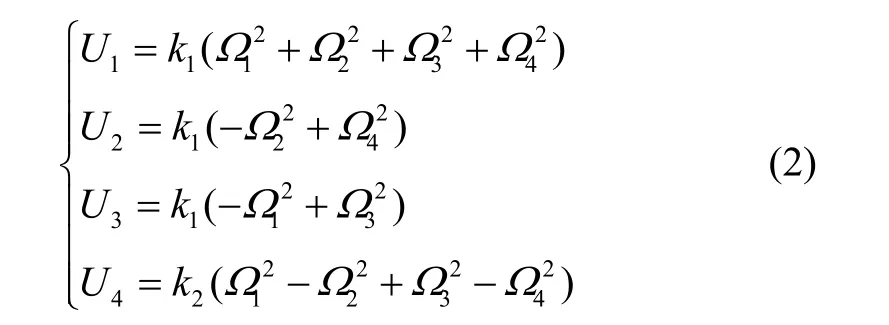
式中：φ、θ、ψ分別為滾轉角、俯仰角、偏航角；M為四旋翼無人機質量； Ω1、 Ω2、 Ω3、 Ω4分別為四個電機轉速；L為旋翼中心到機體坐標原點的距離；k1、k2分別為旋翼的升力和阻力系數；U1～U4分別為垂直、滾轉、俯仰、偏航四個通道的控制量；kx、ky、kz、kφ、kθ、kψ分別為各通道阻力系數； Δx、 Δy、 Δz、Δφ、 Δθ、 Δψ分別表示為有界的干擾或者未建模部分。

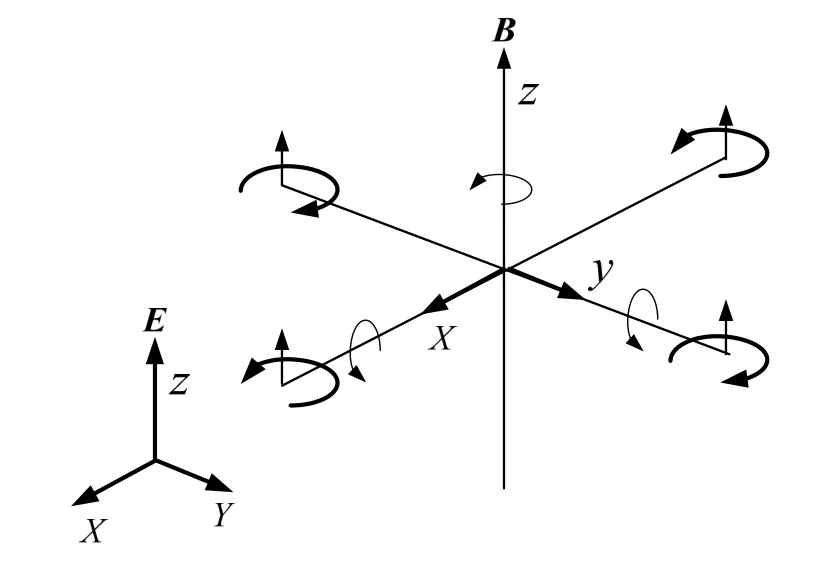
圖1 四旋翼無人機坐標系示意圖Fig.1 Coordinate systems of quadrotor UAV

2 模糊自抗擾控制器設計

從系統的動力學模型可知，四旋翼是一個典型的欠驅動的系統，姿態控制為飛行控制的基礎和關鍵所在。其姿態子系統方程如下：

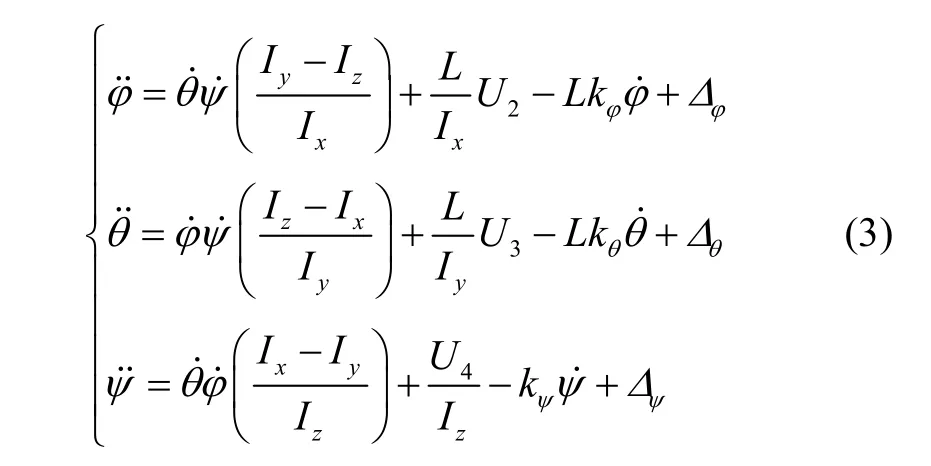
將式(3)整理得：

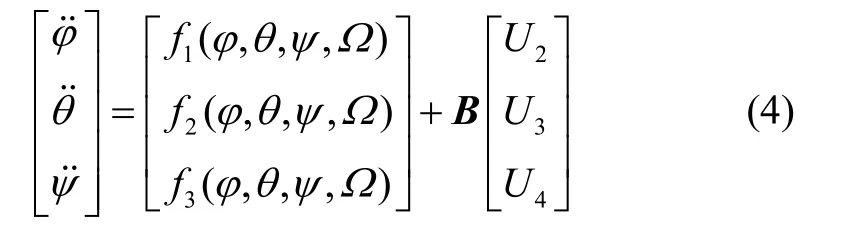
其中，

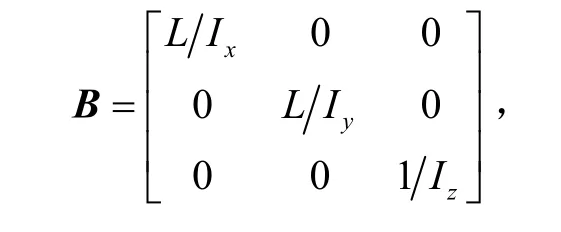
四旋翼的姿態子系統方程是一個多輸入多輸出非線性耦合系統，本文利用自抗擾控制算法中的擴張狀態觀測器對系統耦合部分進行實時跟蹤和估計，并在控制律中進行補償和修正，將多輸入多輸出非線性耦合系統轉變成相對獨立的單輸入單輸出線性子系統。

本文以四旋翼無人機模型中的滾轉角φ為例，描述模糊自抗擾控制器設計過程。

2.1 擴張狀態觀測器設計

根據四旋翼的滾轉子系統數學模型，設 ξ1=φ，ξ2=φ˙，ξ3=f1，并假定 f˙1=h且有界，ξ= [ξ1ξ2ξ3]T。將滾轉角方程表示為狀態向量方程形式：

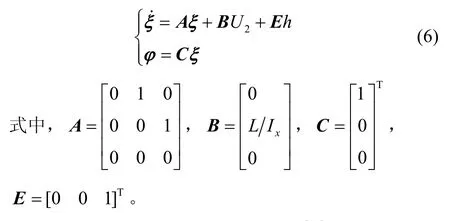
根據式(6)，建立擴張狀態觀測器[15]：

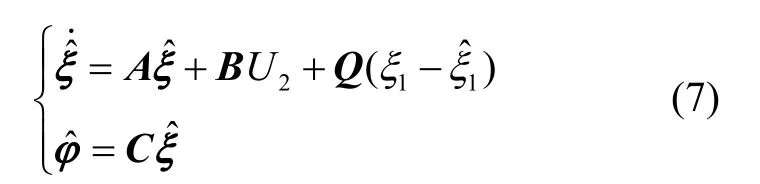
2.2 模糊狀態誤差反饋控制

設期望滾轉角為V1，且一階導數和二階導數存在，分別為V2和。根據經典的 ADRC算法，建立系統的狀態誤差反饋控制律為

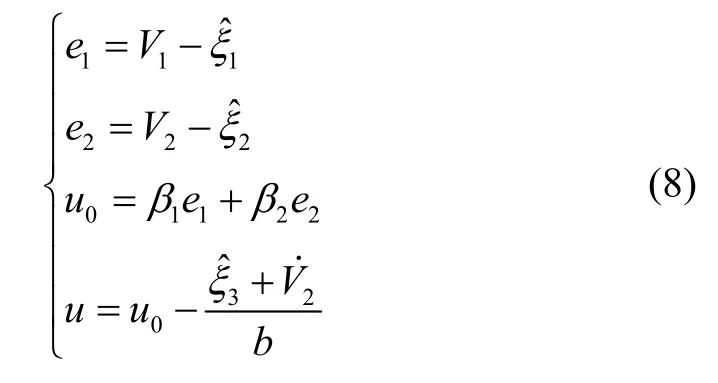
式中：e1、e2分別是誤差及其微分信號；1β、2β分別是誤差反饋控制量的增益系數；b是補償增益；u0為狀態誤差反饋控制器，u為最終控制器。

在實際應用中，狀態誤差反饋參數整定類似于PID控制器的參數整理，需要對不同狀態的控制進行手動調整參數，自適應性較差。為此引入模糊邏輯控制器，利用模糊控制規則，依據e1、e2的變化，得出模糊控制器輸出Δ1β、Δ2β，自動逼近最優，從而提高自抗擾控制器的自適應性，改善控制效果。

設定模糊輸入量為e1、e2，并且在各自論域上定義5個模糊語言子集為{負大(NB)，負小(NS)，零(ZO)，正小(PS)，正大(PB)}，隸屬度函數采用三角形隸屬度函數。模糊推理采用Mamdani型推理，同時根據飛行器姿態可控制性能及自抗擾控制器參數整定方法，制定出Δ1β和Δ2β模糊規則表。

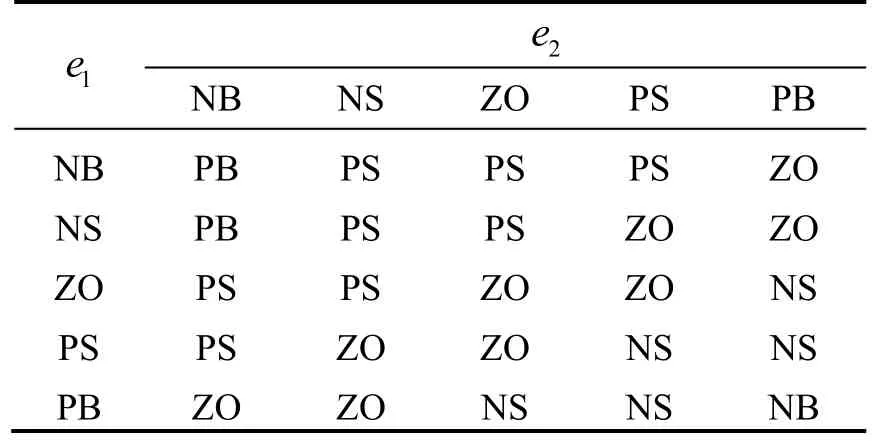
表1 Δ1β模糊規則表Tab.1 Fuzzy rules of Δ1β

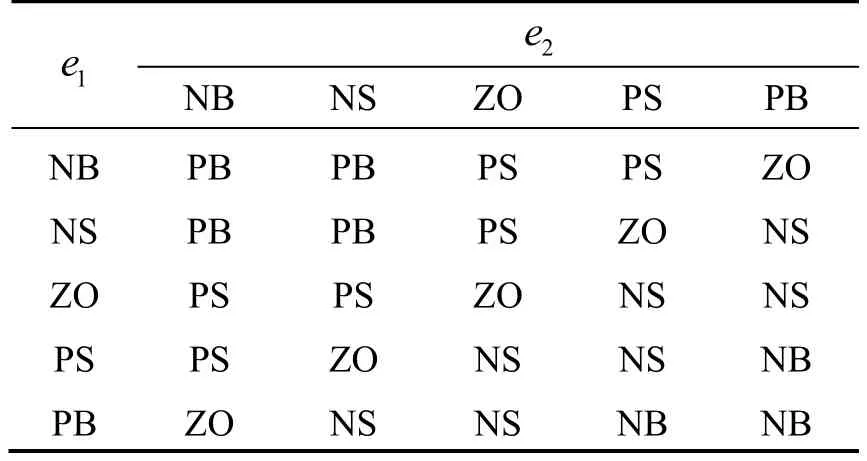
表2 Δ2β模糊規則表Tab.2 Fuzzy rules of Δ2β

依據控制規則，得出最終反饋誤差控制律的增益系數：

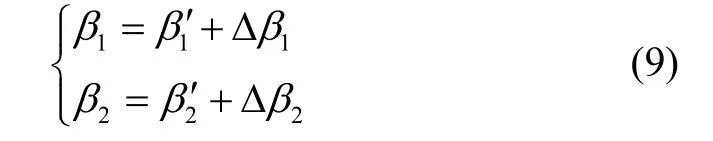
式中，1β′、2β′是狀態誤差反饋初始值。

最后結合ADRC參數整定原則和ADRC公式，即可得到滾轉角的模糊自抗擾控制器。其他兩個通道可以按照同樣方法設計各自控制器。從而可得，基于模糊自抗擾控制器的四旋翼無人機姿態控制系統，其結構原理如圖2所示。

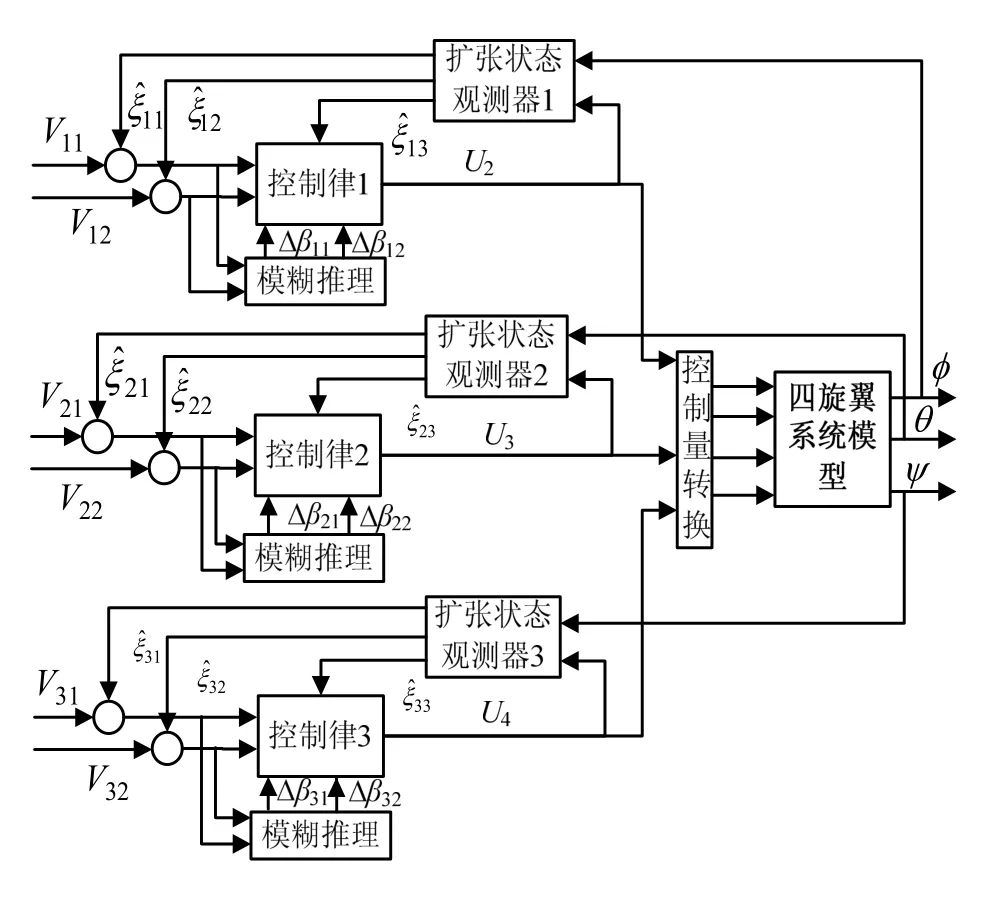
圖2 模糊自抗擾姿態控制結構原理圖Fig.2 Schematic of attitude control based on Fuzzy-ADRC

3 穩定性分析

3.1 擴張狀態觀測器穩定性分析

為了分析簡便，配置觀測器的極點全部位于-ω0，則特征多項式λ(s)可以表示為

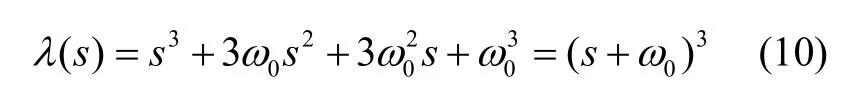
式中，ω0是觀測器的帶寬。觀測器的帶寬越大，估計值就越精確，但是過大的帶寬會增加噪聲的敏感度。觀測器的增益可以表示為

定理1：由于h是有界的，則存在一個常數 σi＞0以及時間T1＞0。如果存在t≥T1，且 ω0＞0，則(i=1,2,3)，從而對于系統的有界輸入，估計誤差是有界的，即閉環系統是漸進穩定的。

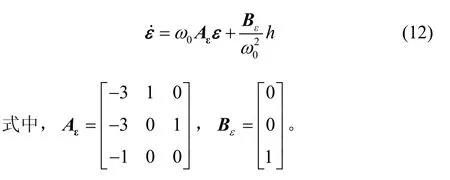
證明：式(12)的解為

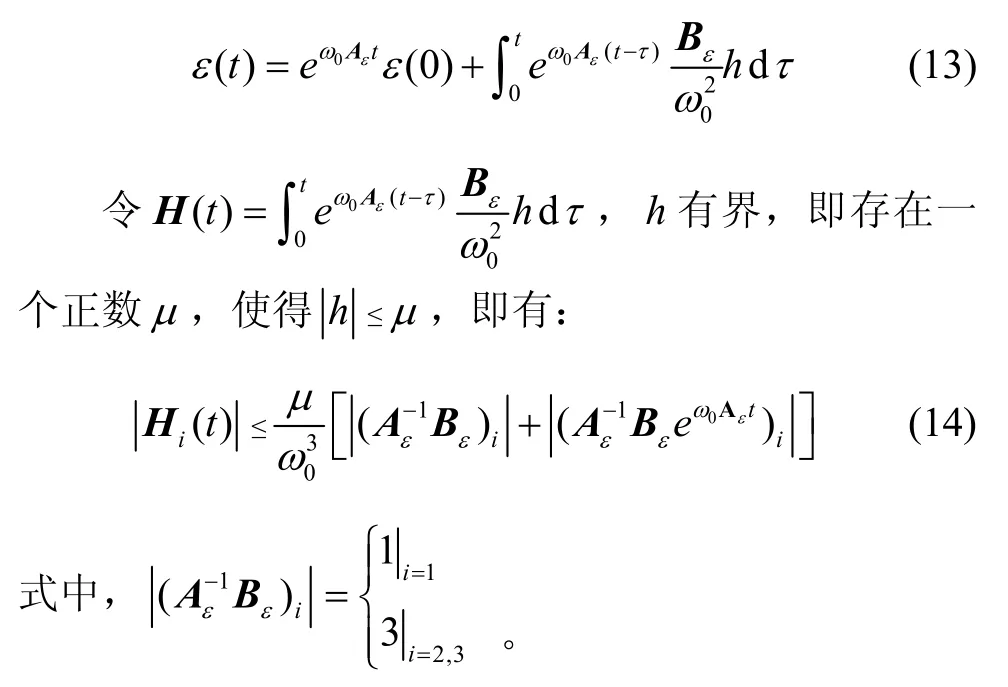
由于 ESO 的三重極點配置在-ω0，則Aε是 Hurwitz穩定的，對于t≥T1＞0，有(i=1,2,3)，即可得：

式中，i=1,2,3。證畢。

3.2 模糊反饋控制器穩定性分析

為了保證設計的模糊反饋誤差控制器是穩定的，采用輸入/輸出(I/O)穩定性理論進行分析。根據I/O穩定性定理，需分別證明系統傳遞函數和模糊反饋控制器分別是鈍性和嚴格鈍性，即可得到系統穩定的充分條件[20]。

由式(6)，可得滾轉角方程傳遞函數為

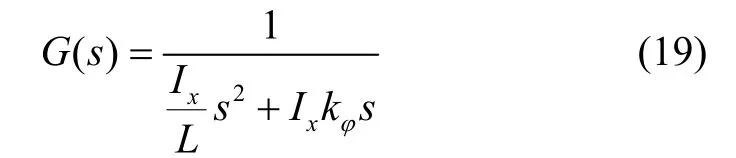
由鈍性定理可知，被控對象G( s)本身本不是鈍性的，對被控對象和控制器分別乘以(s+n)和 (s +n)-1，變換后等效控制對象和反饋控制器的傳遞函數分別為

若滿足Re(G′(jw))≥0，則G′( s)為鈍性，因此有：

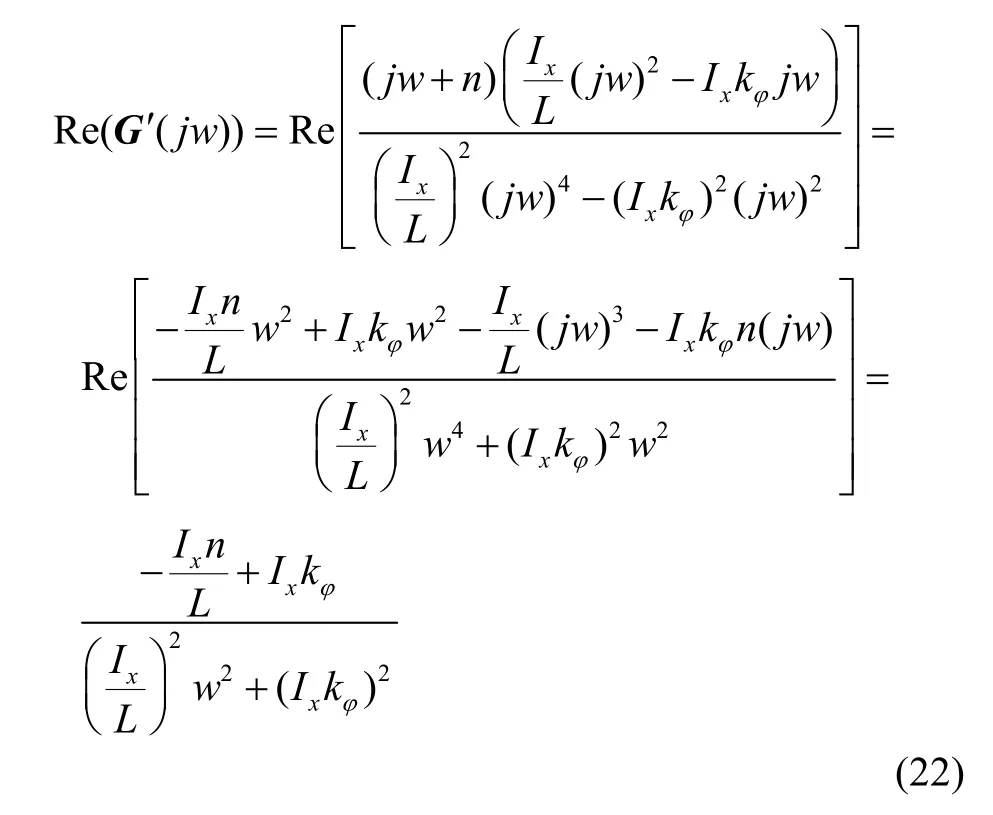
當kφL ≥n時，則Re(G′(jw))≥0，G′(s)為鈍性。

若滿足Re(Gc′( jw))≥μ（其中μ＞0），則G′(s)為嚴格鈍的，因此有：

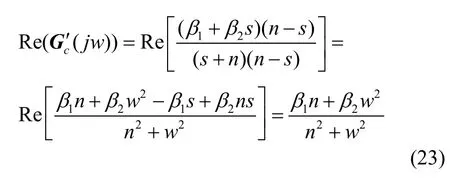
若β1n＞0， β2≥0時，則Re(Gc′( jw))≥μ，G′( s)為嚴格鈍的。

從而可知，本文針對滾轉角設計的模糊反饋誤差控制器，滿足I/O穩定充分條件為

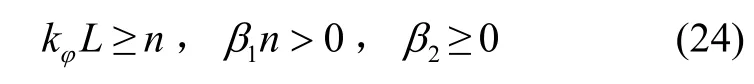
同理，可以推斷出俯仰角和偏航角，滿足I/O穩定充分條件分別為

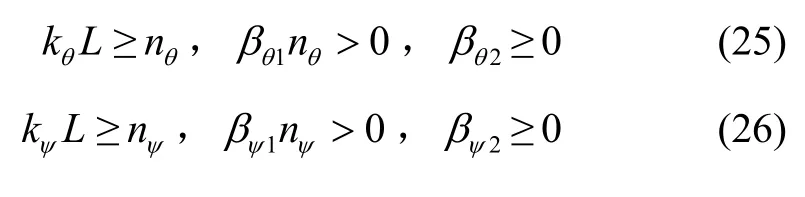
4 仿真對比分析

依據圖 1所建立的四旋翼無人機的數學模型及圖2所示的基于模糊ADRC的姿態控制示意圖進行仿真分析。在仿真中四旋翼無人機的模型參數如表3所示。

模糊自抗擾控制器參數較多，參數整定的結果直接影響控制性能的好壞。經過多次仿真計算，四旋翼模糊自抗擾姿態控制器的主要參數如下：

對應的擴張狀態觀測器的增益分別為

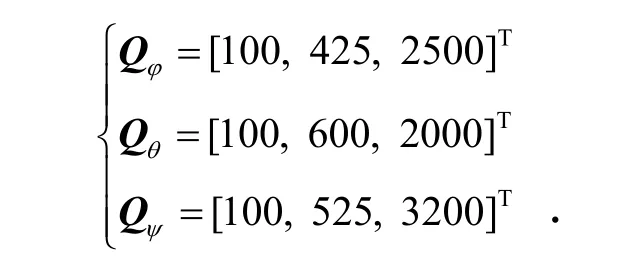
根據推導出的I/O穩定充分條件，可得 ni= 0.0036，i=φ, θ, ψ。反饋控制律增益的初值設置如下：

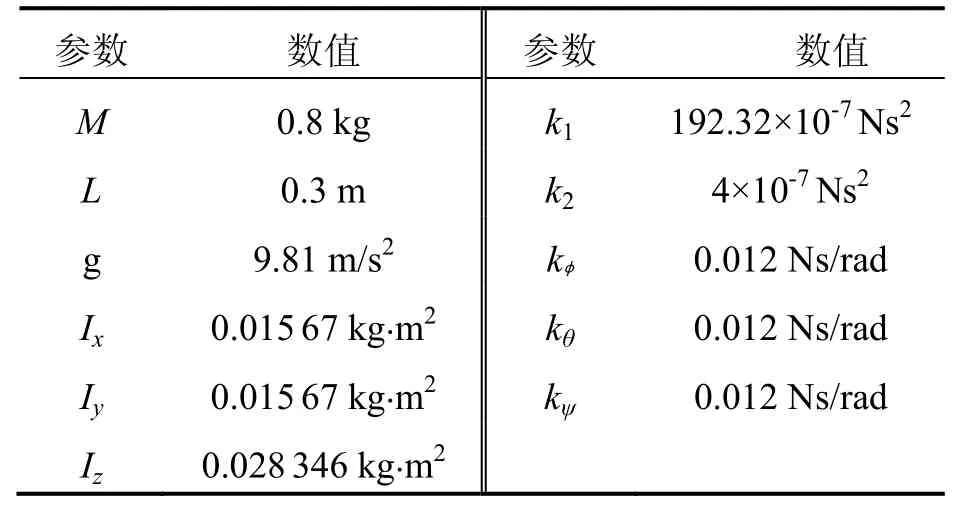
表3 四旋翼無人機模型參數Tab.3 Model parameters of quadrotor UAV

滾轉角、俯仰角、偏航角的期望值設為零；同時設初始值為[φ0,θ0,ψ0]=[3°, 3°, 3°]，且一階導數為零。為了驗證系統的魯棒性，當t=[1.5, 2.5]時，在滾轉通道加入50sin(t)的擾動信號；當t=[3.5, 4.5]時，在俯仰通道加入脈沖擾動信號，幅值為20。通過仿真計算，給出了擴張觀測器及信號跟蹤結果，以及同經典ADRC對比結果。

圖3～5顯示了系統各通道的擴張狀態觀測器對系統各個狀態量及擾動量的估計仿真結果。從仿真結果可以看出，ESO能夠快速的估計和準確的追蹤各通道的狀態變量。由圖3(c)、4(c)可知，在不同通道中分別施加時變干擾信號和脈沖干擾信號時，ESO都能取得很好的追蹤效果，保證了通過擴張狀態變量 ξ?3在控制器中對擾動的實時補償。圖6顯示了各個通道的控制輸入量的變化，從圖6(a)、6(b)可知，在施加干擾時，對應通道的控制輸入量發生變化，但是不會影響其他的輸入量。圖7顯示了不同控制策略下各姿態角的仿真結構比較。從仿真結果可知：在姿態角初始值的不理想狀態下，兩種策略都能在1 s內趨近穩定；但是模糊ADRC相比較于經典ADRC，系統的平均超調量更小，減小約75%，同時在系統遭遇擾動時，干擾造成的輸出波動幅值變化更小，平均降低約30%，顯示了具有更強的抗干擾能力，說明系統具有良好的自適應性。通過仿真結果表明，所設計的模糊自抗擾控制器具有很好的魯棒性、自適應性、穩定性及更佳的抗干擾能力，能對具有強耦合性的四旋翼無人機姿態系統進行有效的控制。

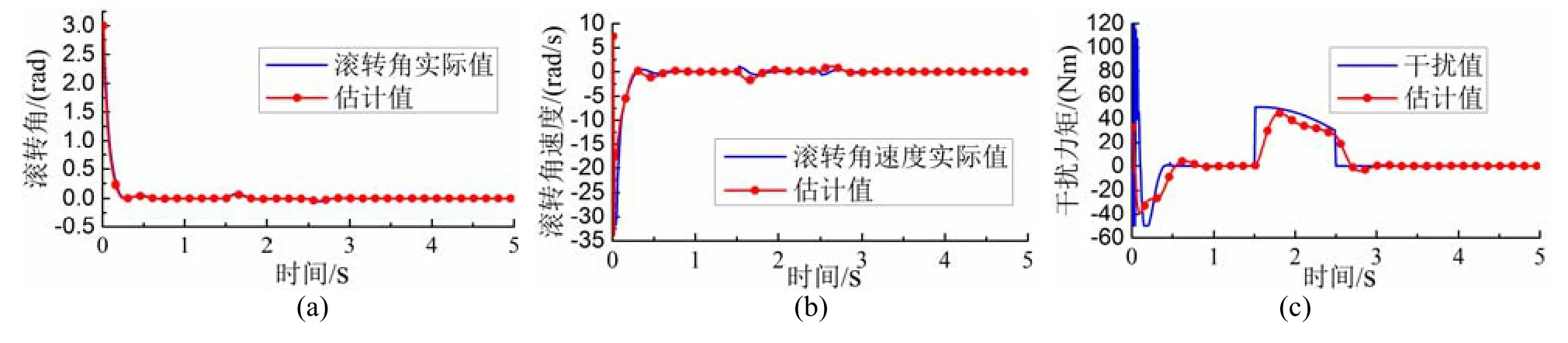
圖3 滾轉角的擴張觀察器觀察結果Fig. 3 Estimation of ESO of roll subsystem

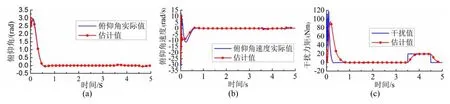
圖4 俯仰角的擴張觀察器觀察結果Fig. 4 Estimation of ESO of pitch subsystem

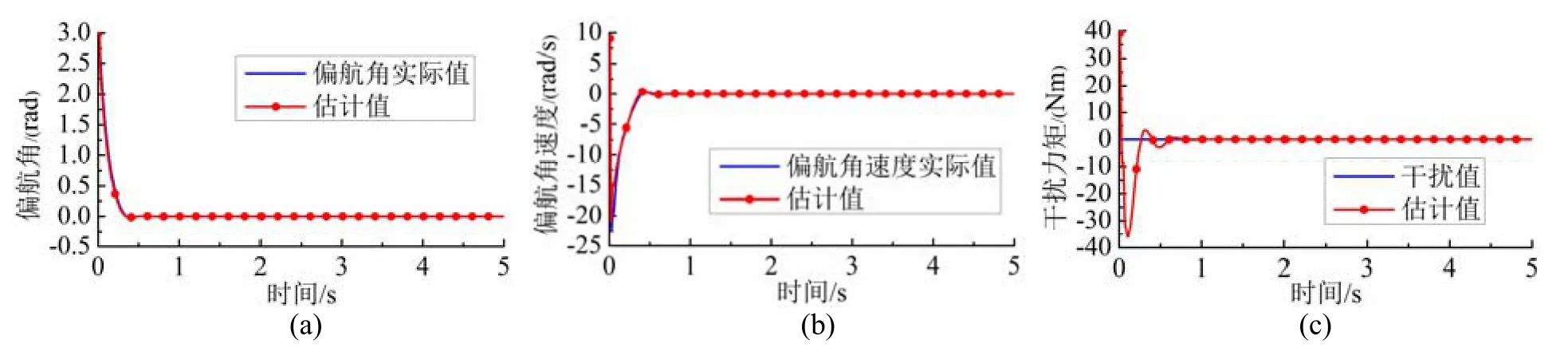
圖5 偏航角的擴張觀察器觀察結果Fig.5 Estimation of ESO of yaw subsystem

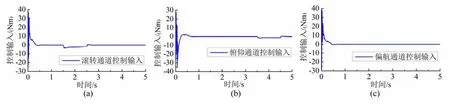
圖6 各通道的控制輸入Fig. 6 Control input of each channel

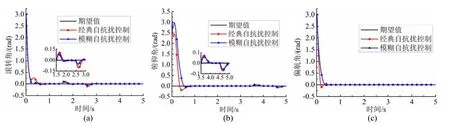
圖7 不同控制策略下各姿態角追蹤對比圖Fig. 7 Contrast of tracking attitude with different control strategies

5 結 論

本文針對四旋翼無人機的姿態系統，設計了一種模糊自抗擾控制器，給出了四旋翼無人機的模糊自抗擾姿態控制器的設計過程。通過理論分析，得出擴張狀態觀測器的估計誤差是有界；同時，根據I/O穩定性定理，給出模糊反饋誤差控制器穩定的充分條件。通過仿真分析，驗證了所設計的模糊自抗擾控制器具有較強的魯棒性、自適應性和抗干擾能力，以及能夠滿足四旋翼無人機的姿態控制要求。

（References）：

[1] Bouabdallah S, Noth A, Siegwart R. PID vs LQ control techniques applied to an indoor micro quadrotor[C]// 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems. Sendal, Japan, 2004: 2451-2456.

[2] Cavalcante Sa R, De Araujo A L C, Varela A T, et al. Construction and PID control for stability of an unmanned aerial vehicle of the type quadrotor[C]//2013 Latin American Robotics Symposium and Competition Conference. Arequipa, Peru, 2013: 95-99.

[3] Colrado J, Barrientos A, Lafaverges B, et al. Miniquadrotor attitude control based on Hybrid Backstepping and Frenet-Serret theory[C]//2010 IEEE International Conference on Robotics and Automation, Anchorage USA, 2010: 1617-1622.

[4] Zhao Bo, Xian Bin, Zhang Yao, et al. Nonlinear robust adaptive tracking control of a quadrotor UAV via immersion and invariance methodology[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 2891-2902.

[5] Islam S, Liu P X, Sanddik A EI. Nonlinear adaptive control for quadrotor flying vehicle[J]. Nonliner Dynamics, 2014, 78(1): 117-133.

[6] Boudjedir H, Bouhali O, Rizoug N. Adaptive neural networl control based on neural observer for quadrotor unmanned aerial vehicle[J]. Advanced Robotics, 2014, 28(17): 1151-1164.

[7] Efe M O. Neural network assisted computationally simple PIλDμcontrol of a quadrotor UAV[J]. IEEE Transactions on Industrial Informatics. 2011, 7(2): 354-361.

[8] 陳彥民, 何勇靈, 孔令博, 等. 四旋翼飛行器分散 PID神經元網絡控制[J]. 中國慣性技術學報, 2014, 22(2): 185-190. Chen Yan-min, He Yong-ling, Kong Ling-bo, and et al. Decentralized PID neural network control for a quadrotor helicopter[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 185-190.

[9] Liu Hao, Xi Jian-xiang, Zhong Yi-sheng. Robust motion control of quadrotor[J]. Journal of Franklin Institute Engineering and Applied Mathematics, 2014, 351(12): 5494-5510.

[10] Lee K, Back J, Choy I. Nonlinear disturbance observer based robust attitude tracking controller for quadrotor UAVs[J]. International Journal of Control Automation and Systems, 2014, 12(6): 1266-1275.

[11] Fernando T, Chandiramani J, Lee T, et al. Robust adaptive geometric tracking control on SO(3) with an application to the attitude dynamic of a quadrotor UAV[C]//2011 IEEE International Conference on Decision and Control and European Control Conference. Denver USA, 2011: 7380-7385.

[12] Khebbache H, Tadjine M. Robust fuzzy backstepping sliding mode controller for a quadrotor unmanned aerial vehicle[J]. Control Engineering and Applied Informatics, 2013, 15(2): 3-11

[13] Liu H, Bai Y Q, Lu G, et al. Robust attitude control of uncertain quadrotors[J]. IET Control Theory Appl, 2013, 7(11): 1583-1589.

[14] Islam S, Liu Xiao-ping P, EI Saddik A. Adaptive sliding mode control of unmanned four rotor flying vehicle[J]. International Journal of Robotics & Automation, 2015, 30(2): 140-148.

[15] 何勇靈, 陳彥民, 周岷峰. 四旋翼飛行器在風場擾動下的建模與控制[J]. 中國慣性技術學報, 2013, 21(5): 624-630. He Yong-ling, Chen Yan-min, Zhou Min-feng. Modeling and control of a quadrotor helicopter under impact of wind disturbance[J]. Journal of Chinese Inertial Technology, 2013, 21(5): 624-630.

[16] 韓京清. 自抗擾控制技術[M]. 北京: 國防工業出版社, 2008: 255-287. Han Jing-qing. Active disturbance rejection control technique[M]. Beijing: National Defence Industry Press, 2008: 255-287.

[17] Tang Shuai, Yang Qiu-hui, Qian Shao-ke, et al. Height and attitude active disturbance rejection controller design of a small-scale helicopter[J]. Science China-Information Sciences, 2015, 58(3): 220201-220217.

[18] Sira-Ramirez H, Linares-Flores J, Garacia-Rodriguez C, et al. On the control of the permanent magnet synchronous motor: An active disturbance rejection control approach[J]. IEEE Transactions on Control Systems Technology, 2014, 22(5): 2056-2063.

[19] Zheng Qing, Dong Li-li, Lee D H, et al. Active disturbance rejection control for MEMS gyroscopes[J]. IEEE Transactions on Control Systems Technology, 2009, 17(6): 1432-1438.

[20] Sio K C, Lee C K. Stability of fuzzy PID controllers[J]. IEEE Transactions on Systems, Man and Cybernetics (Part A: Systems and Humans), 1998, 28(4): 490-495.

Attitude fuzzy active disturbance rejection controller design of quadrotor UAV and its stability analysis

DOU Jing-xin, KONG Xiang-xi, WEN Bang-chun
(School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China.)

To solve the attitude control problems in quadrotor unmanned aerial vehicle (UAV), a quadrotor attitude controller based on fuzzy active disturbance rejection control (ADRC) is designed. At first, the dynamic model of quadrotor UAV is analyzed, and a control scheme based on fuzzy ADRC attitude control algorithm is given. The extended state observer (ESO) and the fuzzy state feedback controller using the above algorithm are designed. The stability analysis shows that the estimation error is bounded, and it also gives the sufficient condition for feedback error’s stability. Simulation results indicate that by using the fuzzy ADRC scheme, the system’s overshoot and the output’s fluctuation are reduced by 75% and 30% respectively when system subjects to disturbance. Therefore, the control system has better anti-disturbance performance and steady state performance, meeting the attitude control requirements of quadrotor UAVs.

quadrotor unmanned aerial vehicle; attitude control; extended state observer; active disturbance rejection control; fuzzy control

V279

：A

2015-07-06；

：2015-12-02

國家自然科學基金項目（51375080）；中央高校基本科研業務費專項資金（N130603003）

竇景欣（1983—），男，博士研究生，從事飛行器非線性控制方面研究。E-mail: doujingxin@163.com

聯 系 人：聞邦椿（1930—），男，教授，博士生導師。E-mail: bcwen1930@vip.sina.com

1005-6734(2015)06-0824-07

10.13695/j.cnki.12-1222/o3.2015.06.022