基于氣浮臺的交會對接模擬及姿態跟蹤控制

黃 成，陳興林，王 巖，周乃新

（哈爾濱工業大學 控制科學與工程系，哈爾濱 150001）

基于氣浮臺的交會對接模擬及姿態跟蹤控制

黃 成，陳興林，王 巖，周乃新

（哈爾濱工業大學 控制科學與工程系，哈爾濱 150001）

針對交會對接中衛星的姿態跟蹤控制問題，設計了一種魯棒有限時間控制算法。首先，設計并采用兩個六自由度氣浮臺模擬交會對接的兩顆衛星，搭建交會對接地面物理仿真系統。其次，應用姿態誤差函數，推導描述氣浮臺追蹤器相對于氣浮臺目標器姿態運動的姿態誤差動力學模型。最后，基于此模型采用反步法思想給出了該控制算法的詳細設計。李雅普諾夫理論推導和仿真結果表明，在存在邊界未知的有界外界擾動的情況下，該控制算法可以使氣浮臺追蹤器在20 s內實現對姿態隨時間改變的氣浮臺目標器的準確跟蹤，并保證系統的穩定性。

氣浮臺；姿態跟蹤；有限時間控制；魯棒性；反步法

在衛星交會對接的操作中，追蹤衛星對于目標衛星的姿態跟蹤是一個非常重要且具有挑戰性的環節，而姿態跟蹤控制策略的好壞將會直接影響跟蹤的效率和準確率，因此對衛星姿態跟蹤控制策略的研究對于交會對接等空間操作是非常必要的[1]。衛星一旦進入軌道，對其控制策略的測試和調整是極其困難和風險極大的，由氣浮臺組成的地面物理仿真系統可以基本模擬衛星在軌運動與控制的實際狀態，能夠進行高置信度的地面物理仿真[2]，因此在在軌操作之前，基于氣浮臺對衛星姿態控制策略的研究和驗證是必不可少的[3]。

過去的幾十年里，國內外許多科研機構對于衛星姿態控制已經展開了大量研究[4]。Lee[5]通過選擇一種姿態誤差函數，提出了一種姿態控制方法，該方法適用于具有大初始姿態誤差的跟蹤系統；Wong[6]基于李雅普諾夫方法設計了一種參數更新的全狀態反饋控制律，解決了編隊飛行中衛星質量不確定的問題；Raymond[7]針對6自由度衛星的編隊控制問題，基于歐拉-拉格朗日系統理論設計了兩種無源性控制器。上述文獻雖然保證了系統的穩定性和收斂性，但只是保證了系統的漸進穩定，即當時間趨于無窮時姿態誤差才會收斂到平衡點，不具有快速收斂性。然而為了實現衛星更高的可操作性，控制策略的快速收斂是必需的，所以動力學系統有限時間穩定性的思想被廣泛的應用到衛星姿態跟蹤控制上。Du[8]設計了一種連續飽和有限時間控制器解決了剛性航天器的全局有限時間姿態穩定問題；Meng[9]提出了分布式有限時間姿態遏制控制方法解決了同時控制多個剛性物體的問題。上述研究雖然應用了有限時間控制思想，但都是基于齊次方法進行的姿態校正控制。另外，外界擾動對系統穩定性的影響不容忽視，而上述文獻均不能對邊界未知的有界外部擾動進行有效抑制。

為了克服這些問題，本文設計了一種能夠在地面進行衛星動力學全物理仿真的六自由度氣浮臺，應用旋轉矩陣和姿態跟蹤誤差函數推導了氣浮臺姿態平臺的姿態誤差動力學模型，基于該模型應用反步法設計了魯棒有限時間姿態跟蹤控制器，通過進行李雅普諾夫理論分析，確保了控制系統的有限時間收斂性、穩定性和對邊界未知的有界外部擾動的魯棒性。

1 交會對接地面物理仿真系統

1.1 系統構成

交會對接地面物理仿真系統用于對衛星控制算法的分析及驗證[10]，主要包括一個表面光滑的花崗巖基礎平臺，兩個可以實現6個自由度氣浮無摩擦運動的六自由度氣浮臺，包括上位機、垂向運動伺服調節系統、速率陀螺儀（用于姿態測量）、質心調節系統、冷氣噴氣裝置、電控系統、執行機構、通信系統等。其中，以氣浮球軸承和重力平衡伺服運動機構為核心的兩個六自由度氣浮臺分別用來模擬目標衛星和追蹤衛星的動力學狀態，氣浮臺目標器與氣浮臺追蹤器配合，實現完整的交會對接動力學與控制的物理仿真實驗。整個系統運行于大型花崗巖平臺上，該平臺為交會對接及以后的編隊衛星等地面物理仿真實驗提供平臺支撐。交會對接地面物理仿真系統如圖1所示。

1.2 六自由度氣浮臺

本文根據交會對接地面物理仿真實驗的需求，設計了可以實現完整6個自由度動力學仿真的六自由度氣浮臺，其整體結構如圖2所示，該氣浮臺包括姿態平臺、水平運動平臺和重力平衡伺服運動機構；根據臺體結構，定義Z向垂直于地平面，X、Y向符合右手定則，Rx、Ry、Rz分別為以X、Y、Z向為轉動軸的轉動方向。姿態平臺由氣浮球軸承支撐，通過相應的控制可以沿Rx、Ry、Rz方向運動，即模擬目標衛星（或追蹤衛星）的姿態調整過程。在進行姿態調整之前，首先要對姿態平臺進行質心調節，即使得系統的質心與旋轉中心重合。為保證系統響應數據反饋的實時性和準確性在質心調節和姿態控制過程中采用陀螺儀作為姿態測量傳感器。水平運動平臺由平面氣浮軸承支撐，底部的3個氣浮軸承可以使整個氣浮系統沿X、Y向無摩擦地運動。

圖1 交會對接仿真系統Fig.1 The rendezvous and docking simulation system

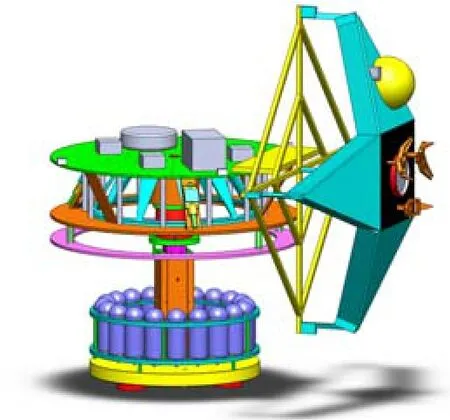
圖2 六自由度氣浮臺Fig.2 The 6-DOF simulator

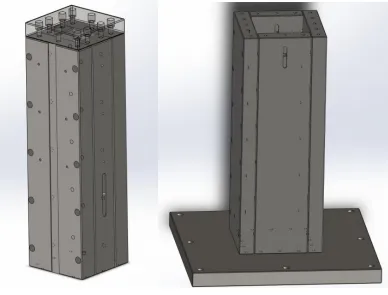
圖3 垂向氣浮軸承結構Fig.3 Structure of vertical air bearing

重力平衡伺服運動機構的垂向運動氣浮軸承由立柱型氣浮軸承外套和內套兩個重要部件組成，結構如圖3所示。根據升降距離，通過控制精密氣浮閥使姿態平臺可以沿著垂向進行無摩擦地升降運動，并定位到指定的位置；該設計使用氣浮軸承而非機械方法實現了重力平衡和垂向漂浮運動，保證了姿態平臺真正意義上的全物理仿真。

2 氣浮臺姿態誤差動力學模型

本文主要模擬衛星交會對接過程中對接停靠階段的姿態跟蹤控制問題，因此這部分只針對六自由度氣浮臺的姿態平臺建立姿態動力學模型和姿態誤差動力學模型，不考慮垂向和水平方向運動對姿態運動的耦合作用，這樣后文中提到的氣浮臺實際是指六自由度氣浮臺的姿態平臺。

2.1 姿態動力學模型

為了更好地研究氣浮臺運動規律，定義慣性坐標系和與氣浮臺固連的本體坐標系原點都固定在氣浮臺旋轉中心，氣浮臺姿態由本體坐標系相對于慣性坐標系的方向表示。特殊正交群(special orthogonal group，SO(3))是由行列式為1的3行3列正交矩陣組成的集合，R表示旋轉矩陣，是由歐拉角 [φθ ψ]T描述的，R ∈SO(3)，即 SO(3)={ R ∈ R3×3|RTR= I , detR =1}。為便于模型推導，本文應用旋轉矩陣R描述氣浮臺姿態[11]。R表示將氣浮臺追蹤器本體坐標系旋轉到慣性坐標系的追蹤器旋轉矩陣。在對氣浮臺進行姿態控制之前，已經完成對氣浮臺的質心調節，因此不用考慮質心與旋轉中心不重合而引起的重力擾動力矩，因此氣浮臺追蹤器姿態運動學與動力學方程如式(1)(2)所示：

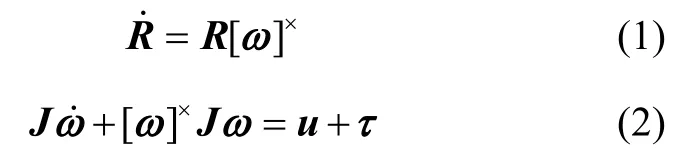
式中： ω∈ R3×1是氣浮臺追蹤器本體坐標系相對于慣性坐標系的角速度在追蹤器本體坐標系中的投影；u ∈R3×1和τ ∈ R3×1分別表示作用于氣浮臺追蹤器的控制力矩和擾動力矩； J ∈R3×3表示追蹤器本體坐標系下的慣性矩陣；[ω]×是對應于角速度的叉乘矩陣，表現形式如式(3)所示：

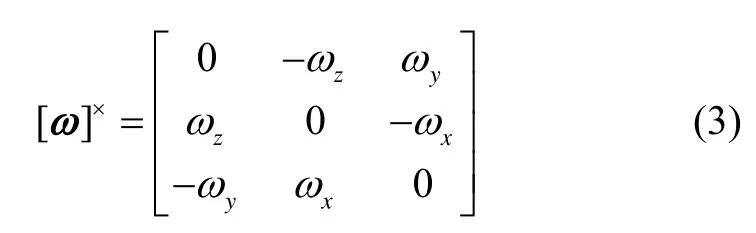
ωe表示角速度誤差，在追蹤器本體坐標系中定義如式(4)所示：

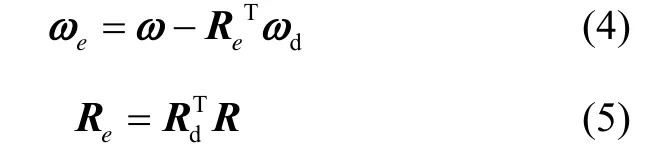
式中：Re∈SO(3)為氣浮臺追蹤器相對于氣浮臺目標器的姿態誤差，定義如式(5)所示，其中 Rd∈SO(3)和ωd∈R3×1分別表示目標器姿態旋轉矩陣和目標器本體坐標系中目標器角速度。

2.2 姿態誤差動力學模型

基于旋轉矩陣設計姿態控制系統的一個關鍵步驟是選取合適的誤差，然而2.1節中定義的姿態誤差和角速度誤差是不能夠直接應用到控制器設計中的。文獻[12]構造了一種姿態誤差函數和姿態誤差向量，其定義如等式(6)和(7)所示：

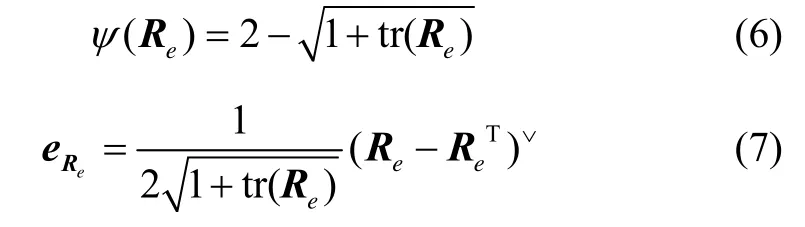
式中：tr(Re)表示姿態誤差矩陣的跡， -1≤ tr(Re)≤3，∨表示叉乘的逆運算。

根據姿態誤差和姿態誤差函數的定義可知，對于確定的Rd，姿態誤差函數可以看成是只關于R的函數；根據等式(7)可知，在集合L={R ∈SO(3)|ψ(Re)＜2}中，姿態誤差向量不會出現奇異點，可以被完整定義。另外根據文獻[12]，姿態誤差函數和姿態誤差向量具有如下性質：

① 在集合L中，姿態誤差函數具有局部二次性，并且滿足

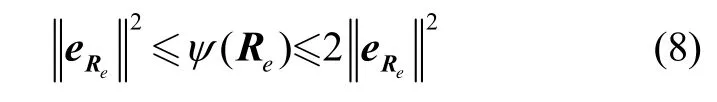
因此本文應用姿態誤差函數，姿態誤差向量和角速度誤差來表述氣浮臺追蹤器相對于目標器的姿態誤差動力學模型。根據運動學方程(1)可得進一步導出姿態誤差Re對于時間的導數為

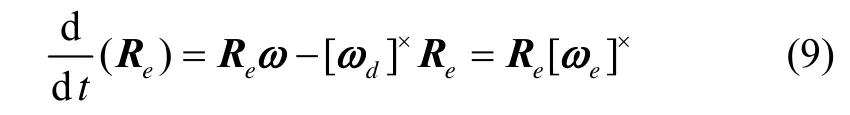
根據叉乘運算的特性 R[ x]×RT=[R x]×和等式(5)，推導出姿態誤差向量 eRe對于時間的導數，即氣浮臺姿態誤差運動學模型：

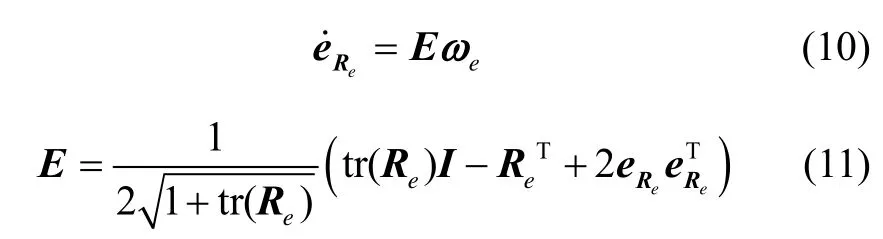
結合等式(9)和等式(5)，對等式(2)進行變換，然后代入 ω= ωe+ReTωd，可得氣浮臺追蹤器相對于目標器的姿態誤差動力學模型如(12)(13)所示。

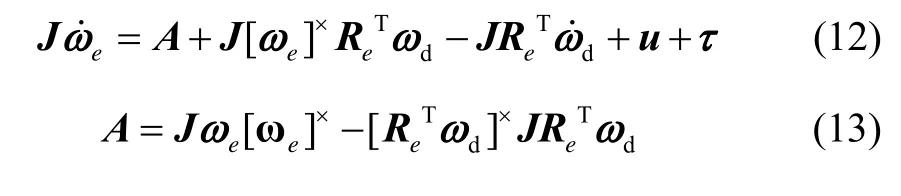
3 控制器的設計

控制器的設計是在保證起始姿態誤差在集合L內的前提下進行的。根據式(10)和式(12)組成的氣浮臺追蹤器相對于目標器的姿態誤差運動學和動力學方程可知，此時該系統是一個標準的級聯系統[13-14]，因此本節應用自適應魯棒控制和有限時間控制的思想，采用反步法設計一種氣浮臺追蹤器姿態跟蹤控制器，為此引入如下變量[15-17]：

根據文獻[18]給出如下兩個引理，并應用到控制器的設計中。

引理1 假設 α1, α2,… ,αn都是正數，0＜ρ＜2，則有下面不等式成立：

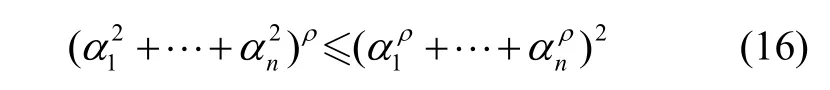
引理2 給定有限時間穩定的擴展李雅普諾夫函數描述：v˙( x)+ αv( x )+ βv(x )γ≤0 (α＞0, β＞0,0＜γ＜1)，設初始狀態 x (0)=x0，則系統在有限時間T內將會收斂到平衡點。

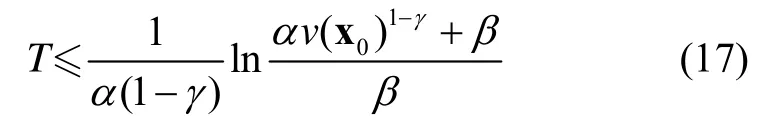
第一步：選取李雅譜諾夫函數：

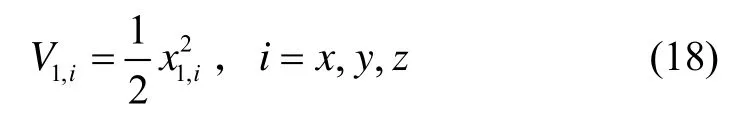
式中： x1=[x1,x,x1,y,x1,z]T，函數兩邊對時間求導得：

根據引理1，結合等式(20)可得：

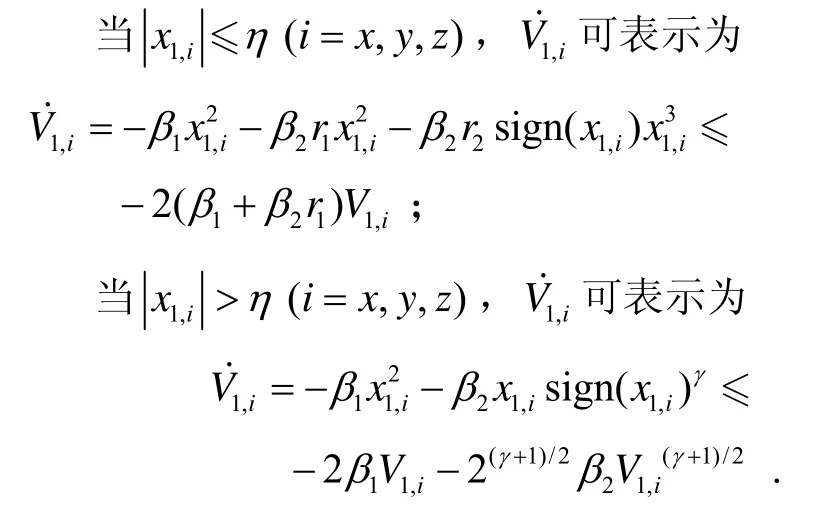
根據引理2可知，x1將在有限時間得收斂到η。第二步：設計自適應有限時間控制律。定義是 τ的邊界估計值，是τ的估計誤差值，Q是正定對角矩陣，選取李雅普諾夫函數因此，當 ωd和有界，采用(25)所示控制律，x1、x2和τ～是有界收斂的。

第三步：證明：存在有界擾動力矩時，控制律u可以保證x1、x2和 ωe在有限時間內收斂到0點。選取李雅普諾夫函數V3。當時，因為η可以為任意小的正常數，x1、x2和 ωe可以在有限時間內收斂到0點附近，因此下面證明只考慮的情況。

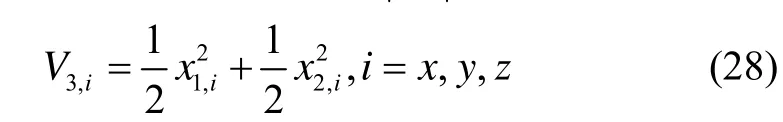
對其求導：

下面將上一步中b1分別與前四項組合。當與第一項組合時，不等式表示為

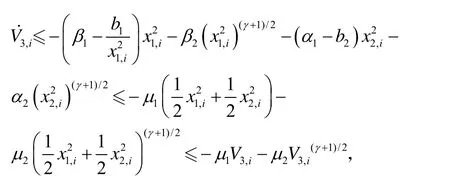
式中：μ1= min(β1- (b1/ x12,i), α1- b2), μ2= min(β2, α2)，認為 μ1＞ 0, μ2＞ 0，根據引理2可知，在有限時間T內x將會收斂到區域1,i將收斂到0點， β越大x越趨11,i近于0點。

同理：b1與第二項組合時，在有限時間T內，x1,i將收斂到區域，x2,i將收斂到0點。β2越大，x1,i就越趨近于0點。

b1與第三項組合時，在有限時間T內，x1,i將收斂到0點，x2,i將收斂到區域。α 越1大x2,i越趨近于0點。

b1與第四項組合時，在有限時間T內，x1,i將收斂到0點，x2,i將收斂到區域。α2越大，x2,i就越趨近于0點。

根據式(15)和(19)，角速度誤差可以表示為

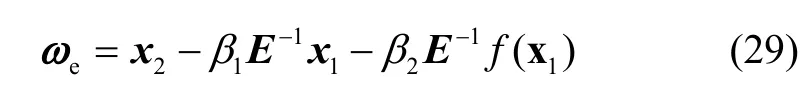
之前已證明x1和x2在有限時間T內可以收斂到0點，根據式(29)的形式可知 ωe在有限時間內也可以收斂到0點。

4 仿真校驗

為了驗證文中基于反步法所設計的魯棒有限時間姿態跟蹤控制器(25)的有效性，在MATLAB/Simulink環境下對氣浮臺姿態跟蹤控制系統進行了仿真研究。仿真中應用的氣浮臺相關數據來源于實驗室已經開發完成的一個五自由度氣浮臺，具有一定的真實可靠性。

氣浮臺慣性矩陣和初始角速度為

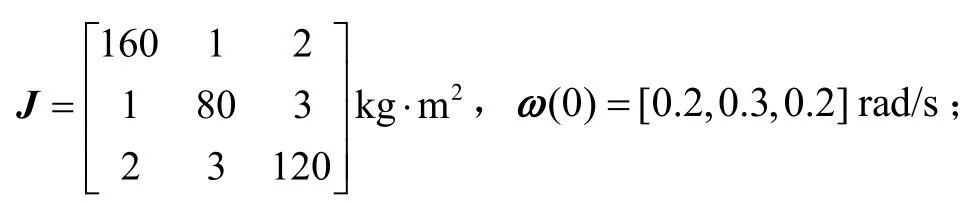
目標角速度為

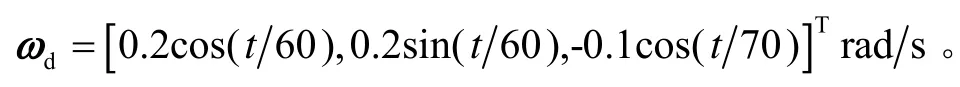
姿態R和目標姿態Rd的初始值結合角速度和目標角速度初始值根據等式(1)給定。

為了實現氣浮臺追蹤器對目標器的姿態跟蹤，控制器(25)的參數選擇如下：γ = 0.5， Q=I， β1=0.02，β2= 0.02， α1=2， α2=4。在控制器(25)作用下，氣浮臺的時間響應曲線如圖4～圖8所示。由圖4～圖6所示的 eRe、x2和 ωe響應曲線可以看出，eRe、x2和 ωe在25 s后趨向于零，因此本文所設計的控制器保證了氣浮臺在有限時間內完成對目標姿態的跟蹤。

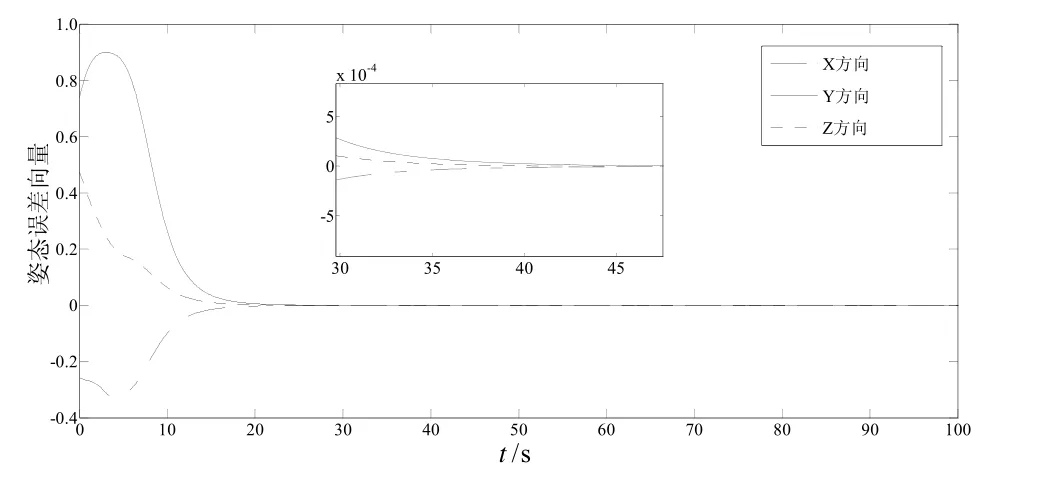
圖4 姿態誤差向量 eRe曲線Fig.4 Curves of attitude error vector

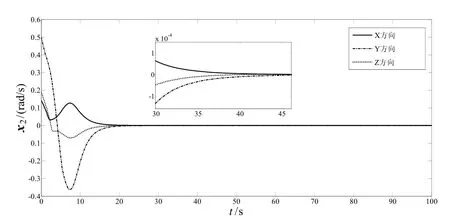
圖5 虛擬輸入誤差x2曲線Fig.5 Curves of virtual import error

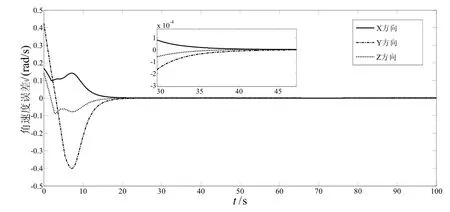
圖6 角速度誤差eω曲線Fig.6 Curves of angular velocity error

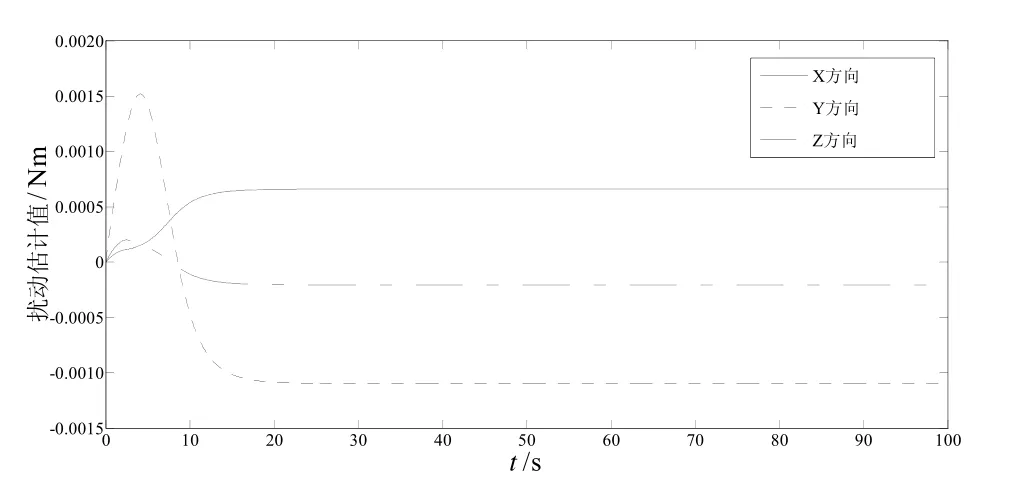
圖7 擾動邊界估計曲線Fig.7 Curves of estimated disturbance value

圖7為擾動力矩邊界值估計曲線，可以看出，控制器在15 s后完成了對邊界未知的擾動力矩邊界值的估計，并基于此進行補償。圖8為姿態誤差函數曲線，可以看出，姿態誤差函數在15 s后趨向于零，且始終屬于集合L，因此姿態誤差向量不會出現奇異點。

從仿真結果可知，采用文中設計的控制器(25)可以保證具有未知邊界擾動的氣浮臺快速地實現對有界目標姿態的跟蹤。

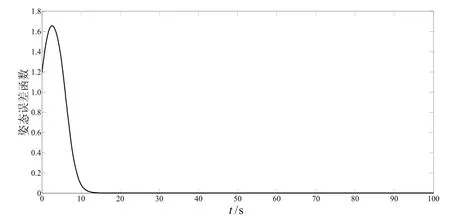
圖8 姿態誤差函數曲線Fig.8 Curve of attitude error function

5 結 論

本文研究了用氣浮臺模擬交會對接過程對接停靠階段的衛星姿態跟蹤控制問題。為了搭建交會對接地面物理仿真實驗系統，設計了能夠實現6個自由度全物理仿真的六自由度氣浮臺。利用姿態誤差函數，推導出氣浮臺追蹤器相對于目標器的姿態誤差動力學模型，并基于反步法，設計了一種魯棒有限時間控制器；采用李雅普諾夫函數證明了該系統的有限時間穩定性和收斂性。仿真結果表明該控制策略保證氣浮臺追蹤器能夠在有限時間內準確地完成對氣浮臺目標器的姿態跟蹤任務，并能夠準確快速地估計出邊界未知的外界擾動的邊界值，具有很好魯棒性，應用前景廣闊。

本文下一步的工作：① 考慮軌道運動和姿態運動的綜合運動，即垂向運動和水平方向運動與姿態運動的耦合運動，模擬衛星交會對接的最終逼近階段運動；② 由于項目進度所限，本文對控制策略的驗證也只是基于氣浮臺數學模型進行了數字仿真研究，因此當實驗條件成熟后，要應用地面物理仿真系統，進行交會對接過程的物理仿真實驗，對提出的控制方法進行進一步的驗證。

（References）：

[1] 林來興. 空間交會對接技術[M]. 北京: 國防工業出版社, 1995.

[2] Schwartz J L, Peck M A, Hall C D. Historical review of air bearing spacecraft simulators[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(4): 513-522.

[3] Agrawal B, Rasmussen R. Air-bearing based satellite attitude dynamics simulator for control software research and development[C]//SPIE Conference on Technologies for Synthetic Environments, 2004: 204-214.

[4] 靳永強, 劉向東, 王偉, 等. 基于模態觀測器的撓性航天器姿態控制[J]. 宇航學報, 2008, 29(3): 844-847. Jin Yong-qiang, Liu Xiang-dong, Wang Wei, et al. Sliding mode attitude control for flexible spacecraft based on modal observer[J]. Journal of Astronautics, 2008, 29(3): 844-847.

[5] Lee T Y. Exponential stability of an attitude tracking control system on SO(3) for large-angle rotational maneuvers[J]. Systems and Control Letters, 2012, 61(1): 231-237.

[6] Wong H. Formation design and nonlinear control of spacecraft formation flying[D]. Polytechnic University, 2006.

[7] Kristiansen R, Nicklasson P J, Gravdahl J T. Spacecraft coordination control in 6DOF: integrator backstepping vs passivity based control[J]. Automatica, 2008, 44: 2896-2901.

[8] Du H B, Li S H. Finite-time attitude stabilization for a spacecraft using homogeneous method[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(3): 740-748.

[9] Meng Z Y, Ren W, You Z. Distributed finite-time attitude containment control for multiple rigid bodies[J]. Automatica, 2010; 46(12): 2092-2099.

[10] Viswanathan S P, Sanyal A, Lee H. Dynamics and control of a six degrees of freedom ground simulator for autonomous rendezvous and proximity operation of spacecraft[C]//AIAA Guidance, Navigation, and Control Conference. 2012: 1-19.

[11] Shuster M D. Survey of attitude representations[J]. Journal of the Astronautical Sciences, 1993, 41(4): 439-517.

[12] Guo Yong, Song Shen-min. Adaptive finite-time backstepping control for attitude tracking of spacecraft based on rotation matrix[J]. Chinese Journal of Aeronautics, 2014, 27(2): 375-382.

[13] 馬廣富, 張海博, 胡慶雷. 基于反步法的主從航天器相對姿態控制[J]. 控制理論與應用, 2012, 29(6): 797-802. Ma Guang-fu, Zhang Hai-bo, Hu Qing-lei. Backsteppingbased relative-attitude control for the leader-follower spacecrafts[J]. Control Theory and Applications, 2012, 29(6): 797-802.

[14] 周麗, 姜長生, 都延麗. 一種基于反步法的魯棒自適應終端滑膜控制[J]. 控制理論與應用, 2009,26: 678-682. Zhou Li, Jiang Chang-sheng, Du Yan-li. A robust and adaptive terminal sliding mode control based on backstepping[J]. Control Theory and Applications, 2009, 26: 678-682.

[15] Bhat S P, Berstein D S. Finite-time stability of continuous autonomous systems[J]. SIAM Journal on Control and Optimization, 2000, 38(3): 751-766.

[16] Reichhartinger M, Horn M. Finite-time stabilization by robust backstepping for a class of mechanical systems [C]//Part of 2011 IEEE Multi-Conference on Systems and Control. Denver, USA, 2011: 1403-1409.

[17] Ding S, Li S. Stabilization of the attitude of a rigid spacecraft with external disturbances using finite-time control techniques[J]. Aerospace Science and Technology, 2009(13): 256-265.

[18] Yu S H, Yu X H, Shirinzadeh B, et al. Continuous finite-time control for robotic manipulators with terminal sliding mode[J]. Automatica, 2005, 41(11): 1957-1964.

[19] Zhang F, Duan G R. Robust integrated translation and rotation finite-time maneuver of a rigid spacecraft based on dual quaternion[C]//AIAA Guidance, Navigation, and Control Conference, 2011: 1-17.

Rendezvous and docking simulation and attitude tracking control based on air-bearing table

HUANG Cheng, CHEN Xing-lin, WANG Yan, ZHOU Nai-xin
(Department of Control Science And Engineering, Harbin Institute of Technology, Harbin 150001, China)

To solve the problem of satellite attitude tracking control in rendezvous and docking, a robust finite-time control scheme is proposed. At first, two six-degree-of-freedom air-bearing tables are designed to simulate the two satellites for rendezvous and docking, and a physical ground simulation system for rendezvous and docking is developed. Then, by using an attitude error function, a dynamics model of the attitude error is established to describe the attitude motion of the air-bearing table tracer relative to the air-bearing table target. Finally, based on the model, the detailed design of the control algorithm is given by using the idea of backstepping method. Lyapunov theory and simulation results show that the air-bearing table tracker can realize in 20s accurate tracking the attitude-variant air-bearing table target for bounded external disturbances with unknown bounds to guarantee the system’s stability.

air-bearing table; attitude tracking; finite-time control; robustness; backstepping method

U666.1

：A

2015-08-03；

：2015-11-13

國家自然科學基金（61174037）；國家自然科學基金創新群體項目（61021002）

黃成（1986—），男，博士研究生，研究方向為高精度運動控制、飛行器控制、智能控制及過程控制。E-mail: huangchengkobe@163.com

聯 系 人：王巖（1972—），男，教授，博士生導師。E-mail: yanw@hit.edu.cn

1005-6734(2015)06-0831-06

10.13695/j.cnki.12-1222/o3.2015.06.023