“雞兔同籠”的解法

楊洋

“雞兔同籠”是我國古代著名的趣題之一。解決“雞兔同籠”問題，通常采用列表法和假設法。采用假設法，可以假設都是雞，那么兔的只數=（腳的總數-雞兔總數€酌恐患Φ慕攀﹢鰨恐煌玫慕攀恐患Φ慕攀Φ鬧皇？雞兔總數-兔的只數；也可以假設都是兔，則雞的只數=（雞兔總數€酌恐煌玫慕攀諾淖蓯﹢鰨恐煌玫慕攀恐患Φ慕攀？

【題目】雞兔共有40只，雞和兔的腳共有112只。雞和兔各有多少只？

【分析與解】這是一道基本的“雞兔同籠”問題，有多種解法。

解法一 假設法。假設都是雞，那么一共有腳40€？=80（只），比實際少112-80=32（只）。用一只兔去換一只雞，可以增加（4-2）只腳；要增加32只腳，需要用32€鰨？-2）=16（只）兔去換雞。所以，兔有16只，雞有40-16=24（只）。

假設都是兔，那么一共有腳40€？=160（只），比實際多160-112=48（只）。用一只雞去換一只兔，可以減少（4-2）只腳，所以雞有48€鰨？-2）=24（只），兔有40-24=16（只）。

小提醒：假設都是雞，先算出的是兔；假設都是兔，則先算出的是雞。

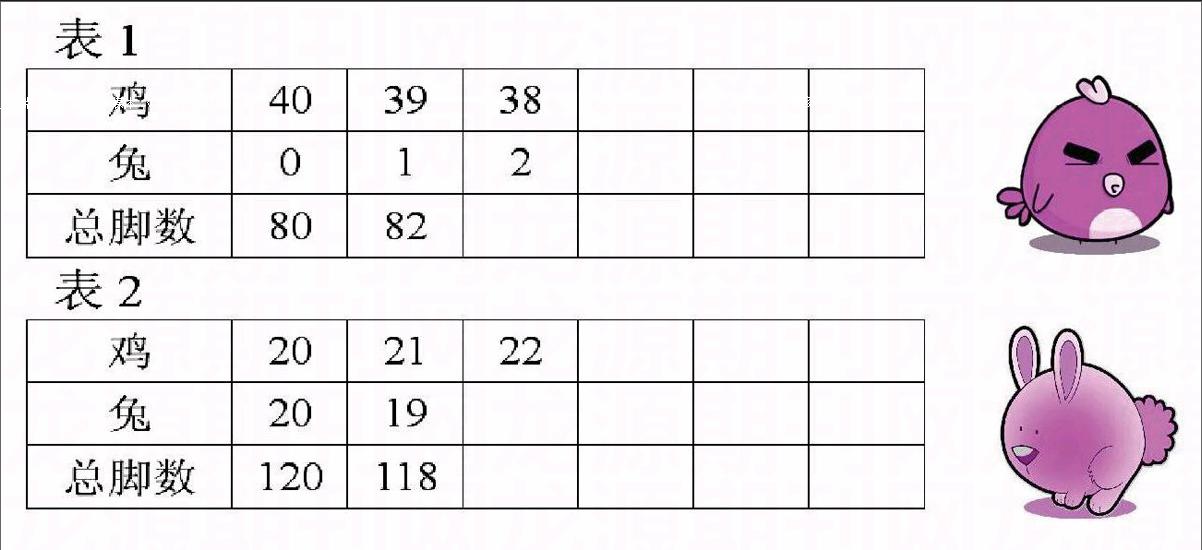
解法二 列表法。如果雞兔總數較少，可以列如下表1找答案；像本題雞兔總數較多，可以從雞兔各占一半算起。如下表2，雞、兔各有20只，共有腳120只，比實際112只略多，所以應增加雞減少兔。你能接著填表找出答案嗎？

解法三 “除減”法。如果每只雞都是“金雞獨立”，一只腳站著；每只兔像人一樣用兩只腳站著，那么落地的腳數還有112€？=56（只）。這時每只雞一只腳，每只兔兩只腳。只要兔多一只，腳的總數就比頭的總數多1，所以兔有56-40=16（只），雞有40-16=24（只）。這種算法，只做一次除法和一次減法就能算出兔子的只數了，很簡單。但如果“腳數”不是4和2（如：三輪摩托車和四輪小汽車的“腳數”分別是3和4），就不能用這種算法了。

聰明的小讀者，“雞兔同籠”問題的解法你學會了嗎？下面請你來露一手吧！

1.養殖場里養了豬和鵝共27只，一共有86條腿。養殖場養了（ ）頭豬，（ ）只鵝。

2.一次數學競endprint