多塔斜拉橋在主震-余震序列波下地震位移研究
王征南 楊浩林 龐于濤 袁萬城
(同濟大學土木工程防災國家重點實驗室,上海200092)
1 引言
現今工程抗震學認為,地震對結構的破壞主要是由結構側向需求引起的結果,因而總是基于結構在主震中的非線性峰值位移來進行評估。然而,橋梁等結構在遭受地震時,總是會歷經前震、主震與余震等一系列地震波動。
余震具有以下幾個特點[1]。首先,地震具有叢集的特征。主震發生之后通常伴隨著余震,主震震級越高,余震對結構的破壞越大。其次,余震強度的大小與主震發生后的時間并沒有關聯。在主震后的很長一段時間里,大震級的余震都有可能發生。再者,余震的數量比較大。如中國汶川大地震,里氏8.0級主震后至今共發生了超過5.0級的余震31次。2010年2月27日在智利中南部地區發生的里氏8.8級地震,發生超過5.0級的余震306次,其中超過6.0級的余震21次。此外,小震級的余震也可能產生大峰值加速度的地震波。如1983年加到福利亞Coalinga地震的余震產生了0.43 g的峰值加速度,超過主震0.31 g的峰值加速度。2004年日本Niigata地震的余震產生了0.15 g的峰值加速度,超過主震的0.1 g的峰值加速度。
主震之后至余震發生之前,橋梁結構由主震所造成的殘余位移無法及時復原,大數量的余震將直接作用在已經具有初始位移的結構上,即使余震震級通常比主震低,也很可能會進一步增加結構的殘余位移,甚至導致落梁的發生。另一方面,在主震之后至余震發生前,結構受到主震的損傷同樣無法及時修復,余震直接作用在已受到破壞的結構上,可能會使構件中產生塑性鉸,造成結構的損傷積累[2],從而對結構造成進一步的破壞。因而余震的存在可能會使結構的地震需求超過主震時期,結構在地震中發生的震害很可能來源于余震的影響。可以說,余震對于結構安全有著不可忽略的影響。
學界已對主震-余震序列影響下結構的響應進行了研究[3-6],先驅學者 Mahin[3]將 1972 年Managu地震后實測的主震-余震波序列作為輸入,研究了單自由度體系的響應在余震下的變化,發現結構的延性位移需求在余震后發生了明顯的增加。Amadio等[4]采用將相同地震動連續數次輸入非線性單自由度體系,研究多次重復中等強度地震對結構的影響程度,研究結果表明,連續遭遇數次地震動的結構反應明顯大于只經歷一次地震動的反應。Lee與 Li等[5]對主震-余震序列下多自由度體系的非線性響應進行了研究,發現將主震波放大或縮小作為余震波會高估結構峰值位移。Hatzigeorgiou等[6]對4個規則與4個不規則框架在5條實測序列波與40條人工序列波下的響應進行了分析,發現在實測序列波下結構的位移延性需求明顯增加。然而多數研究并未涉及橋梁結構領域。由主震引發的具有殘余位移的橋梁,特別是對于在本文中用于工程實例的多塔斜拉橋,由于初始條件的改變,位移需求也會不同,因而在進行橋梁抗震時有必要考慮余震的影響。
本文以一工程實例多塔斜拉橋為背景,建立有限元分析模型,選擇了6條實測的主震及余震波[7],合成主震-余震序列波,來研究強余震對于結構的殘余位移以及位移峰值的影響。
2 地震波
在實際地震中,通常較大的地震都會引發多次余震,即結構實際上所承受的并不是單一地震,而是一個地震序列波。然而根據目前的抗震規范,大部分結構的設計只采用單個地震波進行建模和分析;目前的多塔斜拉橋抗震性能研究也只使用單一的人工地震波檢驗,并沒有考慮到多重地震對結構抗震的影響。但是使用這種設計方法,可能會發生結構可以通過人工波的檢驗卻無法通過主震-余震序列波的檢驗的情況。因此,本文采用主震-余震序列波來對結構進行抗震性能研究。
2.1 選波原則
通常將一次地震的前震和余震作為一次地震能量釋放的起點和終點。為了研究強余震對結構造成的破壞,本文中主震-余震序列波的選取主要基于以下三個原則[8]:
(1)主震震級大于或等于5.5,余震震級大于或等于 4.0。
(2)加速度時程均來自于處在自由場的測站或者場地內具有較小的建筑。
(3)最強余震與主震的加速度峰值之間比例大于或等于0.7。
基于上述幾條原則,本文選擇并形成6條主震-余震序列波,這些波均來自于PEER強震數據庫。
2.2 主震與余震地震波的整合
為了便于研究,本文將相同地震的主震波和余震波整合成為一條地震序列波,相鄰地震動之間間隔100 s,地震序列波在100 s的間隔中加速度為0,目的是使結構由主震所引起的震動在余震發生之前停止。合成后的主震-余震序列波加速度時程曲線見圖1。在分析中只考慮地震縱向輸入。
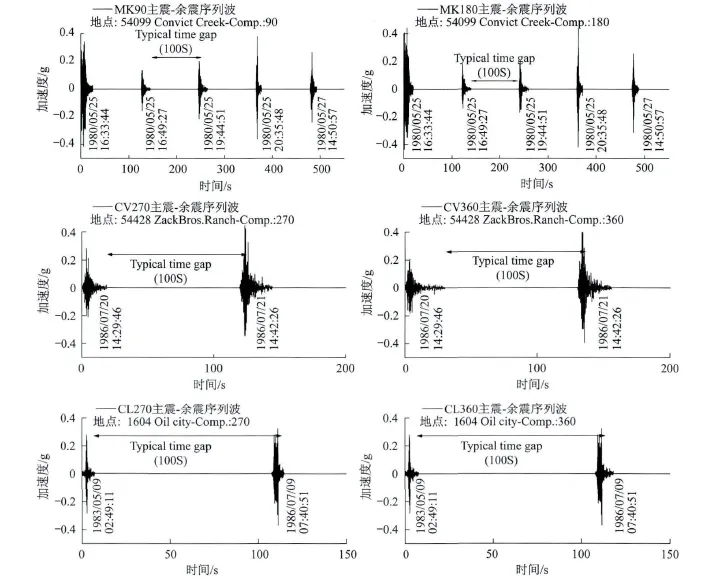
圖1 主震-余震序列波Fig.1 Mainshock-aftershock sequences
3 有限元模型
本文以某一采用塔梁固結體系的多塔斜拉橋為工程背景,該橋主橋跨徑布置為79 m+5×150 m+79 m。主橋為六塔斜拉橋,橋寬為37 m,兩側引橋均為連續梁橋,跨徑布置為50 m跨徑連續梁橋。主梁采用鋼-混凝土組合梁結構,其中鋼材采用Q345-D。斜拉索材料采用 φ15.24 mm鋼絞線,波形鋼腹板PC箱梁橋中的混凝土部分采用C50混凝土,塔身采用C60混凝土,墩身采用C50混凝土,承臺采用C40,鉆孔樁采用C35水下混凝土,承臺封底采用C20混凝土。主橋采用了波形鋼腹板形式,目的在于合理減輕自重、提高預應力鋼束的應力效率。結構采用減隔震體系,結構初始支座布置見圖2,支座采用球型鋼支座,支座剛度為550 000kN/m,屈服力為1 100 kN,支座力-位移關系曲線見圖3。主塔關鍵截面及其下部結構示意圖見圖4和圖5,主塔兩側共18對索,中間段梁上基本索距為7m,塔上索距在1.5~2 m。
計算采用SAP2000有限元程序[9]建立全橋空間有限元模型,建立全橋動力計算模型時,考慮相鄰橋梁的耦聯振動影響,南、北側引橋為連續梁橋模型。在有限元分析模型中,主梁、主塔以及橋墩均采用梁單元模擬;斜拉索采用空間桁架單元,并運用Ernst公式考慮索因自重導致的垂度效應所造成的彈性模量的折減;球型鋼支座采用plastic-Wen非線性連接單元模擬;主橋群樁基礎對應的邊界條件取最低沖刷高程,在承臺底部采用六彈簧(6×6剛度矩陣)模擬樁基和樁土共同作用。考慮主塔和斜拉索的P-Δ效應[10],采用恒載軸力進行了剛度修正。斜拉橋全橋空間有限元模型見圖6。
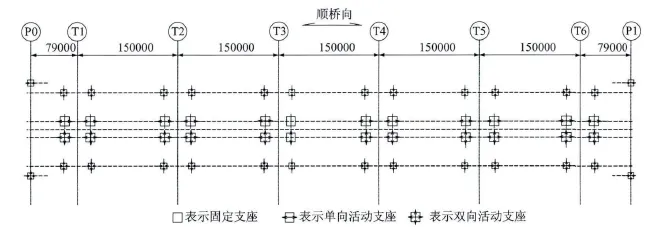
圖2 初始支座布置(單位:mm)Fig.2 The initial bearing arrangement(Unit:mm)
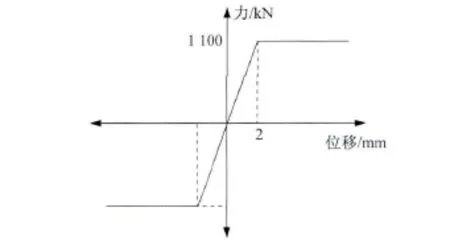
圖3 球型鋼支座力-位移關系曲線Fig.3 The initial bearing arrangement
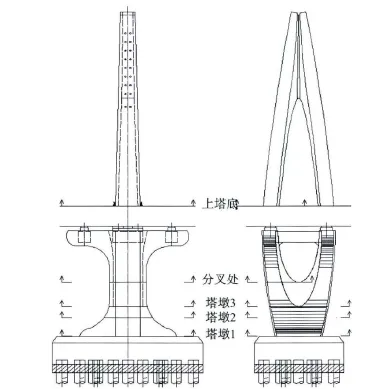
圖4 橋塔關鍵截面Fig.4 The key section of bridge tower

圖5 主塔下部結構立體圖Fig.5 Stereo diagram of tower substructure
圖6 全橋動力模型Fig.6 The dynamic calculation model of the bridge
4 計算結果及分析
從抗震角度來講,塔梁固結體系的多塔斜拉橋可以看成是上部為塔梁固結整體、下部為橋墩、中間用支座連接的連續梁橋。目前,在地震工程基于概率的PEER第二代性能分析框架的發展中,逐漸開始將結構在地震作用下的支座位移作為衡量結構抗震性能的重要性能指標。因而,本文將殘余位移及位移峰值作為抗震性能指標,通過對結構輸入主震-余震序列波來研究余震對于結構抗震性能的影響。考慮到結構采用減震體系,經驗算后得出在上述地震下橋墩與樁基礎均未達到屈服,構件并未發生損傷,變形仍在彈性范圍內,因此本文在研究余震對結構抗震性能的影響時,不需要將墩與樁基礎的地震響應作為衡量余震對結構抗震性能影響的指標,而只需考慮支座位移。地震波輸入方向為縱向輸入,地震主震-余震序列波中主震峰值加速度統一調整為0.5 g。
4.1 支座累積殘余位移
為了分析余震對支座位移的影響,本文選取Mammoth Lakes地震、Chalfant Valley地震以及Coalinga地震等場地共6條實測主震-余震序列波,并對結構進行地震分析。得到結構在考慮上述主震-余震序列波時主梁的支座位移時程曲線(圖7),并列出結構在MK90地震、CV270地震以及CL270地震的三條主震-余震序列波下支座殘余位移的累積情況(表1)。
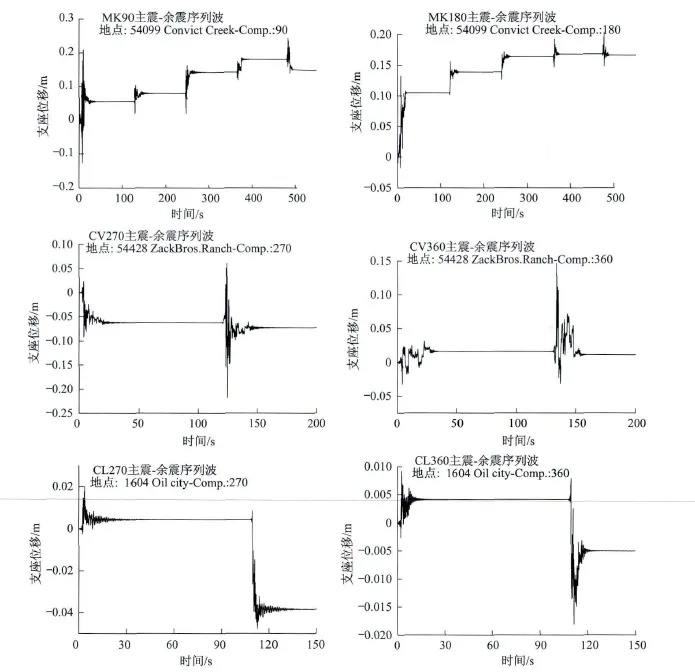
圖7 地震位移響應時程Fig.7 Seismic displacement time history curves
從圖7中各圖中的位移時程曲線及表1中的支座累積殘余位移給出的結果可以看出,與結構只經歷主震相比,考慮余震后結構殘余位移又發生了很大改變。例如,表1中MK90在主震之后殘余位移為0.055 m,經歷前三次余震后殘余位移增大至0.181 m,第四次余震后殘余位移又減小至0.148 m,此時的殘余位移是主震后殘余位移的2.69倍。可見強余震在很大程度影響了結構震后的殘余位移,如果在橋梁結構設計時,不考慮殘余位移的累積,支座的位移能力需求可能會出現不足的情況,結構可能會偏不安全。因此余震對于結構殘余位移的累積是不可忽視的問題,考慮到余震對支座殘余位移的積累影響,有必要在抗震設計中輸入地震波時考慮主震-余震序列波。
另外,由圖7可以看出余震可能會增大殘余位移也可能減小殘余位移,由此可見余震對于結構的抗震性能的影響具有不確定性。因此在橋梁結構抗震設計時,有必要輸入主震-余震序列波,以確定結構在考慮余震時的位移需求。
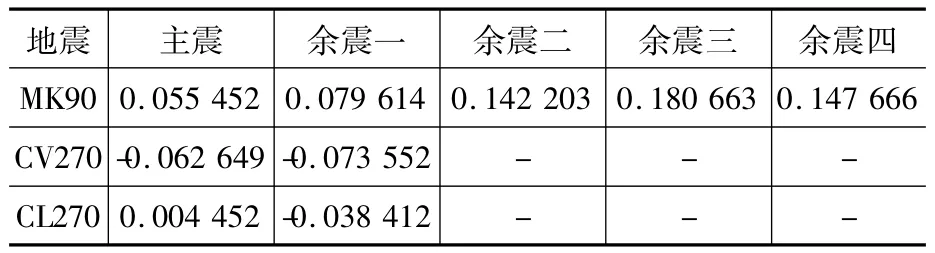
表1 支座累積殘余位移Table 1 The cumulative seismic residual deformation m
4.2 支座位移響應峰值
為了考察殘余位移對支座位移峰值的影響,圖8給出了結構在主震-余震序列波下的主震及各余震的結構位移峰值,即考慮殘余位移累積下的位移峰值。由于結構變形仍在彈性范圍內,結構在以上地震中并未發生損傷,因此可以通過結構在主震-余震序列波下的位移時程(圖7),得到結構不考慮殘余位移時的位移時程。具體方法為將結構在主震-余震序列波中某條余震波下的位移時程減去當次余震發生前的結構殘余位移。表2給出了結構在上述主震-余震序列波中各主震及余震不考慮殘余位移時的位移峰值,并在最后一列附上結構在主震-余震序列波下的位移峰值,用以比較殘余位移的影響。
結合表2與圖8可以看出,結構在主震-余震序列波作用下的位移峰值往往會大于任何單次的主震或余震作用下的位移峰值。如MK90地震中,不考慮殘余位移累積時主震的位移峰值為0.209 m,各余震單獨作用下位移峰值也均不超過0.1 m,但是在主震-余震序列波下,由于殘余位移的累積影響,結構在余震四時的位移峰值達到該地震序列波的最大值0.243 m。可見即使余震震級可能小于主震,余震對結構的位移響應可能比主震小,但在考慮殘余位移累積后,結構在余震下的位移峰值有可能同主震的位移峰值十分接近,甚至大于主震的位移峰值。此外圖9給出了結構在CV270、CV360、CL270以及CL360等地震的主震與主震-余震序列波下的位移峰值比,得出序列波峰值與主震峰值比值在 1.962 08和4.482 07之間。經線性擬合后得到序列波峰值與主震峰值比均值在2.83左右。由此可以看出在某些情況下,在考慮殘余位移的累積后,強余震對結構的位移峰值將有著顯著的影響。綜合表2、圖8、圖9可以看出,主震及余震所產生的殘余位移及其累積效應對于結構的位移峰值有著很大程度的影響。
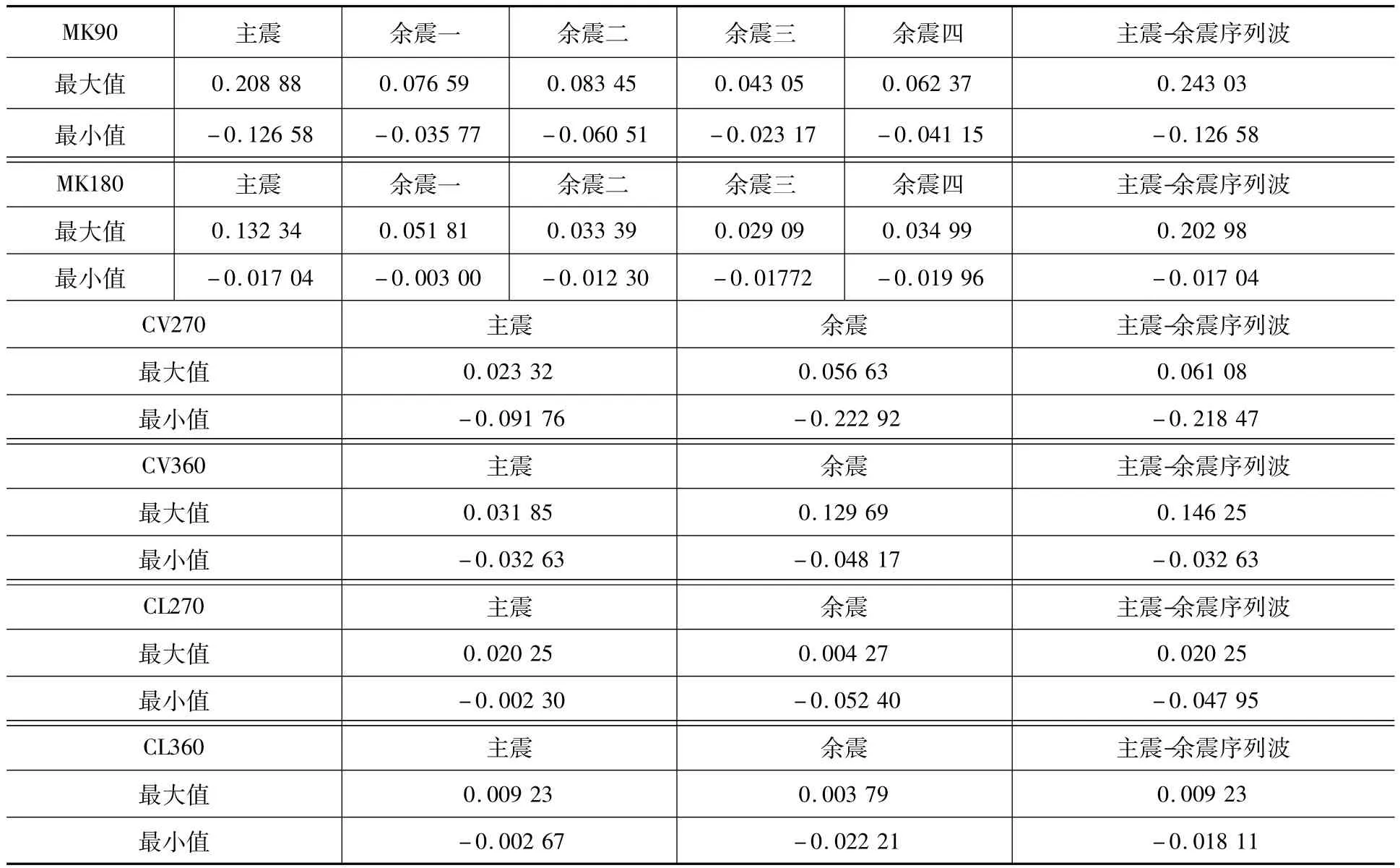
表2 不考慮殘余位移累積時支座位移峰值Table 2 Peak displacement of bearing irrespective of cumulative seismic residual deformation m
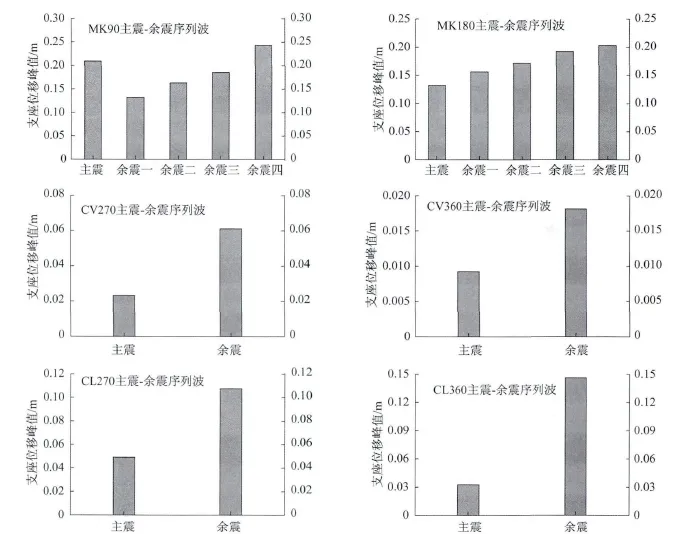
圖8 支座位移峰值柱狀圖Fig.8 The histogram of peak displacement of bearing
因此在設計支座允許位移時,余震及殘余位移累積對于結構支座位移峰值的影響不可忽略,即使支座設計可以滿足主震的位移需求,結構也并非一定是安全的,在考慮余震作用下結構仍然具有落梁的風險,因此在輸入地震波時需要考慮主震-余震序列波。
5 結論
強余震一般作用在經歷主震后仍未修復的結構上,考慮殘余位移累積后,余震在很大程度上會影響結構的位移峰值。在強余震作用下,橋梁抗震設計中支座最大位移即使達到主震的要求,也依然具有落梁的風險,結構在地震中發生的震害很可能來源于余震的影響。因此在橋梁結構抗震設計中將位移作為衡量結構性能的指標時,為了使所確定的結構位移需求更加接近于實際,在地震波輸入時不應僅僅考慮主震,而是應當考慮主震-余震序列波。
主震之后至余震發生前,橋梁結構由主震所產生的殘余位移無法及時復原,考慮殘余位移累積的影響,即使余震震級通常比主震低,余震的存在仍然可能會使結構的地震位移需求超過主震時期。因此,有必要考慮采取措施來限制強余震及殘余位移積累對位移的影響。

圖9 主震與主-余震序列波殘余位移峰值比Fig.9 The ratio between the seismic residual deformation under only the mainshock and under mainshockaftershock sequences
余震對結構殘余位移的影響具有不確定性,它既有可能增大殘余位移,也可能減小殘余位移。因此為了得到結構在考慮余震時的位移需求,建議采用概率方法,對結構輸入大量的主震-余震序列波,并對支座位移進行概率需求分析,以得到最經濟的設計方案。
[1] Ruiz-García J,Negrete-Manriquez J C.Evaluation of drift demands in existing steel frames under as-recorded far-field and near-fault mainshock-aftershock seismic sequences[J].Engineering Structures,2011,33(2):621-634.
[2] 周知,錢江,黃維,等.復雜結構在重復地震序列作用下的損傷性能研究[J].結構工程師,2013,29(4):76-81.Zhou Zhi,Qian Jiang,Huang Wei,et al.Damage of complex structures under repeated sequences of seismic loads[J].Structural Engineers,2013,29(4):76-81.(in Chinese)
[3] Mahin S A.Effects of duration and aftershocks on inelastic design earthquakes[C].Proceedings of the 7th World Conference on Earthquake Engineering,1980,5:677-680.
[4] Amadio C,Fragiacomo M,Rajgelj S.The effects of repeated earthquake ground motions on the non-linear response of SDOF systems[J].Earthquake Engineering and Structural Dynamics,2003,32(2):291-308.
[5] Li Q,Ellingwood B R.Performance evaluation and damage assessment of steel frame buildings under main shock-aftershock earthquake sequences[J].Earthquake Engineering Structural Dynamics,2007,36(3):405-427.
[6] Hatzigeorgiou G D,Beskos D E.Inelastic displacement ratios for SDOF structures subjected to repeated earthquakes[J].Engineering Structures,2009,31(11):2744-2755.
[7] Alliard P M.Mainshocks and aftershocks sequences database[J].2006.
[8] Zhang S,Wang G,Sa W.Damage evaluation of concrete gravity dams under mainshock-aftershock seismic sequences[J].Soil Dynamics and Earthquake Engineering,2013,50:16-27.
[9] 北京金土木軟件技術有限公司,中國建筑標準色合計研究院.SAP2000中文版使用指南[M].北京:人民交通出版社,2008.Beijing Civil King Software Technology Co.,Ltd,China building standard design institute.Chinese user guide for SAP2000[M].Beijing:China Communications Press,2008.(in Chinese)
[10] 李亮,李國強,陳軍武.某鋼結構氣象塔在時程風荷載作用下考慮P-Δ效應的動力時程分析[J].結構工程師,2009,25(4):91-95.Li Liang,Li Guoqiang,Chen Junwu.Dynamic time history analysis of a steel meteorological tower under time history wind load[J].Structural Engineers,2009,25(4):91-95.(in Chinese)

