量子光學中的蒙特卡洛方法研究
王碩


摘要:研究量子光學現象,通常歸結為研究光場與原子的相互作用問題。在本文中,我們利用蒙特卡洛方法模擬了單原子系統的演化過程。我們將單原子系統的演化分為非厄米哈密頓量作用下的演化和隨機性的量子躍遷,并在這兩個過程進行的每一個時間步長后對波函數進行歸一化。根據產生隨機數的“指示”,得到了原子系統單次和系綜平均后所經歷的演化過程。
關鍵字:量子光學,蒙特卡洛方法
中圖分類號:O242 文獻標識碼:A文章編號:1672-3791(2015)05(c)0000-00
1引言
量子光學是以輻射的量子理論研究光的產生、傳輸、檢測及光與物質相互作用的學科,它最初是從量子電動力學理論中發展、演變而來的。它既是量子電動力學理論的一個重要分支,又是激光全量子理論深入發展的結果。同時,量子光學還構成一門新興的應用基礎性學科—光子學的理論基礎。
20世紀60年代激光的問世大大地推動了量子光學的發展,在激光理論中建立了半經典理論和全量子理論。半經典理論把物質看成是遵守量子力學規律的粒子集合體,而激光光場則遵守經典的麥克斯韋電磁方程組。在全量子理論中,把激光場看成是量子化了的光子群,這種理論體系能對輻射場的量子漲落現象以及涉及激光與物質相互作用的各種現象給予嚴格而全面的描述。對激光的產生機理,包括對自發輻射和受激輻射更詳細的研究,以及對激光的傳輸、檢測和統計性等的研究是目前量子光學的主要研究課題[1]。
研究量子光學現象,一般總是歸結為研究光場與原子相互作用問題。在很多場合下,可以看做是二能級原子與光場的相互作用。當光場或原子或光場與原子組成的系統有能量損失的時候,通常采用熱庫理論,即將該系統能量的損失認為是與外界作用的結果,這作用外界比較大,但對其狀態一般不加細致研究,只認為其自由度遠比系統多,因此稱為熱庫。處理熱庫與系統的相互作用常有兩種方法,一是在相互作用繪景或薛定諤繪景中,將整個系統的密度算符方程對熱庫變數求跡,給出系統約化密度算符滿足的主方程,將熱庫變數消去,然后利用密度算符的準幾率表示,將主方程轉化為C數的福克—普朗克方程,最后求解;二是在海森堡繪景(算符變化,態矢不變)中通過噪聲算符將熱庫作用轉變為隨機力,引入量子的朗之萬方程,然后再求解[2]。
近年來,蒙特卡洛(Monte Carlo)方法,或稱計算機隨機模擬方法,被引入量子光學中來研究小系統與熱庫耦合的模擬演化。蒙特卡洛方法是一種基于“隨機數”的計算方法。為了得到具有一定精確度的近似解,所需試驗的次數是很多的,通過人工方法作大量的試驗相當困難,甚至是不可能的。因此,蒙特卡洛方法的基本思想雖然早已被人們提出,卻很少被使用。直至電子計算機的出現,使得人們可以通過電子計算機來模擬隨機試驗過程,把巨大數目的隨機試驗交由計算機完成,并首先在核武器的試驗與研制中得到了應用。蒙特卡洛方法是以概率統計理論為基礎的一種方法,由于它能夠比較逼真地描述事物的特點及物理實驗過程,解決一些數值方法難以解決的問題,因而該方法的應用領域日趨廣泛。
在本文中,我們將主要討論在量子光學中,如何利用蒙特卡洛波函數方法來模擬單個原子系統的演化過程,并給出了二能級原子在蒙特卡洛波函數方法模擬過程中的單次演化以及其系綜平均后的演化過程。
2理論推導
用蒙特卡洛方法模擬波函數的演化,可以把系統的演化分解為幾種可能的波函數,在 時間內,原子有可能發生躍遷,假設發生躍遷的概率為 ,躍遷到各個可能態的概率分別為 ,那么波函數在這段時間內究竟選擇何種波函數,我們就可以用蒙特卡洛波函數方法來模擬。
首先,在[0,1]區間內產生隨機數ε,如果ε> ,說明波函數沒有發生躍遷;如果ε< ,說明發生了量子躍遷,進一步的,通過判斷ε落入哪一個概率區間,可以判斷發生了何種躍遷。這就是用蒙特卡洛方法模擬隨機數演化的基本思想。
一個小系統的蒙特卡洛波函數演化包括兩個過程:非厄米哈密頓量作用下的緩慢演化和隨機性的量子躍遷,并在這兩個過程進行的每一個時間步長后對波函數進行歸一化[3-5]。
假設在t時刻二能級原子的狀態可以用如下波函數表示:
(1)
我們容易得到,在 時間內,發生躍遷的幾率為 (其中, 是單位時間的躍遷幾率)由于 非常小,故在觀察的時間內,躍遷的幾率還是非常小的。為了確定波函數的演化方向,我們在[0,1]內取均勻分布的隨機數ε,一般情況下 ,對應的是沒有躍遷的情況,這時只有波函數的演化,哈密頓量為
(2)
是激光的頻率和原子躍遷頻率的差; 是拉比頻率,表征著偶極子 的原子和光場的耦合。在哈密頓量的作用下,波函數演化
如果 ,對應發射一個光子的情況。這時候,原子產生自發輻射,躍遷到基態
重復以上過程,我們就可以來模擬波函數隨時間的演化過程[4]。
3結果分析與討論
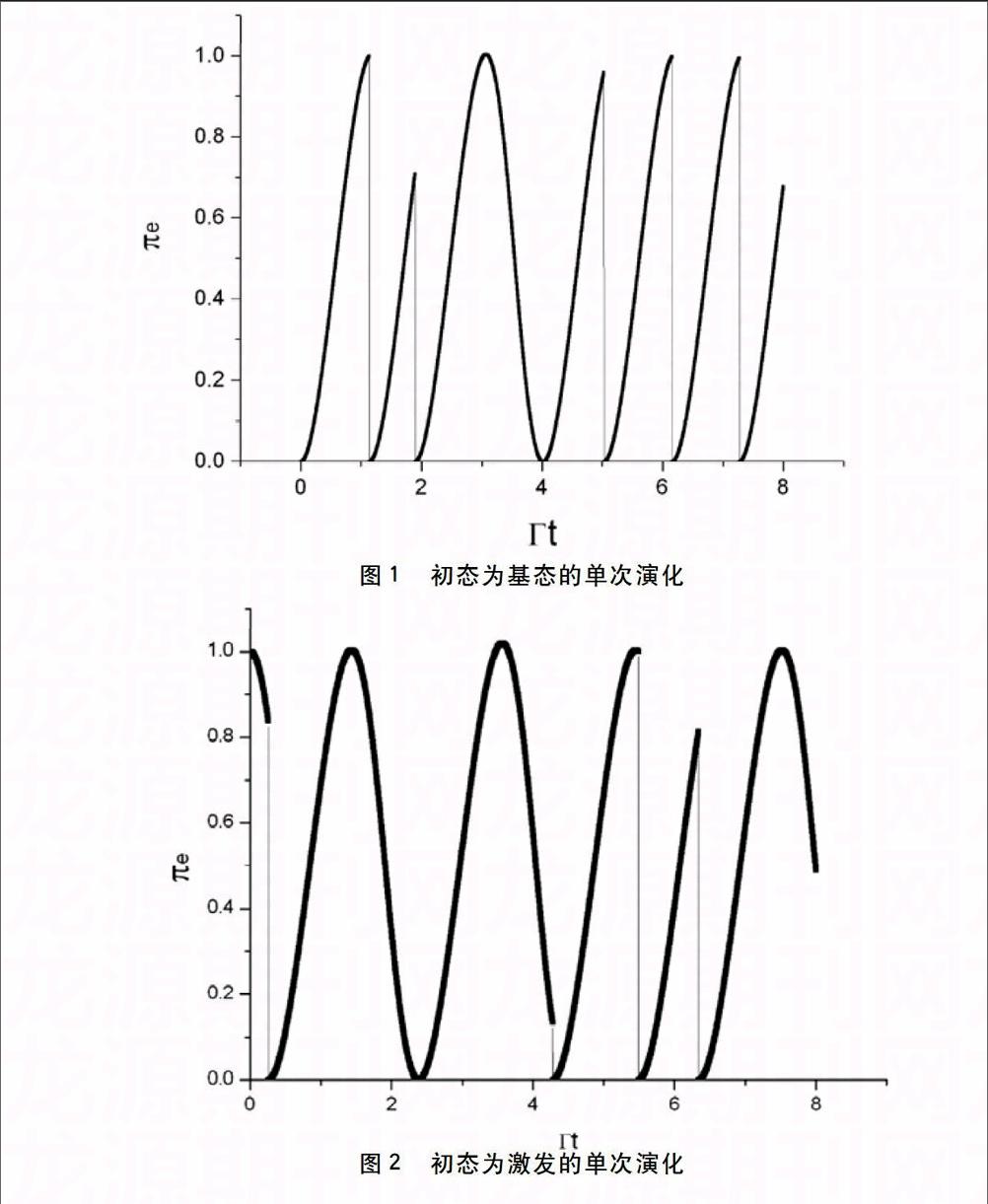
本節中,我們利用蒙特卡羅波函數方法來模擬原子初始分別處于基態 (圖1)、激發態 (圖2)以及疊加態(圖3)時,原子處于激發態的布局數隨時間的演化過程。在以下各圖中,我們令 來表示原子處于激發態的布局數。為了計算方便我們取相應的參數 。
圖1:單次模擬過程,原子處于激發態的布局數隨時間的演化,原子初始處于基態 ,相應參數為
圖2:單次模擬過程,原子處于激發態的布局數隨時間的演化,原子初始處于激發態 ,相應參數為
圖3:單次模擬過程,原子處于激發態的布局數隨時間的演化,原子初始處于疊加態,相應參數為
在圖1、圖2和圖3中,大致描繪了系統處于激發態的幾率隨時間的演化過程。由于原子的躍遷是一個隨機過程,某一時刻是否擁有較大幾率不能保證在此時刻發生躍遷,這可以從圖中直接的顯現出來。斷點處代表原子在此刻發生了躍遷,波函數迅速回到基態。容易理解,初態的改變并不影響演化的大致行為。
上面討論的是一個二能級原子系統在單次隨機過程中的波函數演化,重復以上操作N次然后求系綜平均,就可以得到一個二能級原子系統的演化過程。在圖4和圖5中,我們給出了原子處于基態(圖4)和激發態(圖5)時激發態的布局數隨時間的演化過程。
由圖4和圖5可以看出,隨著演化過程的進行,系統處于激發態的幾率首先呈現一定的振蕩趨勢,最后逐漸趨于0.5。躍遷幾率也趨于穩定。
圖4:系綜平均之后,原子處于激發態的布局數隨時間的演化,原子初始處于基態 , 運行次數 ,相應的參數分別為
圖5:系綜平均之后,原子處于激發態的布局數隨時間的演化,原子初始處于激發態 ,運行次數 ,相應的參數分別為
4總結
近年來,量子光學領域已取得了一系列重大進展和輝煌成就,量子光學的研究對象之一就是小系統與耗散場的相互作用。在本篇論文中,我們運用蒙特卡洛模擬方法分析了單原子系統在耗散場中的演化情況。此演化過程包括兩個部分:非厄米哈密頓量的演化和隨機性的量子躍遷,并在每個時間步長后對波函數進行歸一化。這樣,我們得到了任意時刻系統的波函數。從得到的圖中可以直觀的看出系統躍遷發生的時間點以及躍遷幾率的變化趨勢。最后,我們還給出了系綜平均后原子系統的演化過程。
參考文獻:
[1] M.Orszag. Quantum Optics Including Noise Reduction, Trapped Ions, Quantum Trajectories, and Decoherence [M]北京:科學出版社,2007.5-7.
[2] 楊伯君.《量子光學基礎》[M]北京:北京郵電大學出版社,1996.22-26.116.
[3] K.Mǒlmer, Y.Castin, J.Dalibard. Monte Carlo wave-function method in quantum optics[J]J.Opt.Soc.Am.A 10,524(1993).
[4] J.Dalibard, Y.Castin, K.Mǒlmer. Wave-Function Approach to Dissipative Processes in Quantum Optics[J]Phys.Rev.Lett.68,580(1992).
[5] H.J. Carmichael, An Open System Approach to Quantum Optics, Lecture Notes in Physics(Springer,Berlin,Heidelberg,1993); also: L.Tian, H.J. Carmichael, Phys.Rev.A 46,6801(1992).

