立體幾何中判斷線、面位置關(guān)系的三大利器

福建省南平市光澤縣光澤一中 芮科明

立體幾何中線、面的位置關(guān)系包括線與線、線與面、面與面之間的平行或垂直關(guān)系，這里面的關(guān)系錯綜復(fù)雜，而高考選擇、填空題常常會在這里面做文章，令很多考生頗感頭疼。掌握好下面三大利器，可以讓同學(xué)們贏得信心，真正做到考場上得心應(yīng)手、十拿九穩(wěn)，這三大利器就是：牢記定義、定理；重視幾個常用的結(jié)論；合理使用舉反例法。下面分三點來逐一加以說明。

一、牢記定義、定理

為了使思路更加清晰，可以借助下面的網(wǎng)絡(luò)圖。

對于線、面的平行關(guān)系，有下面的網(wǎng)絡(luò)圖，如圖1。

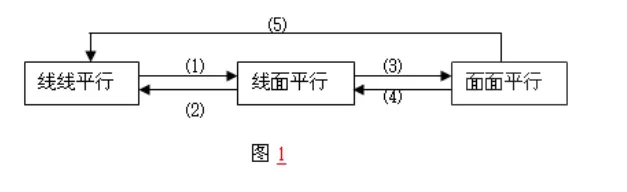
序號（1）～（5）分別代表以下判斷定理或性質(zhì)定理.

第一，線面平行的判定定理：如果平面外的一條直線和平面內(nèi)的一條直線平行，那么這條直線和這個平面平行。

第二，線面平行的性質(zhì)定理：如果一條直線和一個平面平行，經(jīng)過這條直線的平面和這個平面相交，那么這條直線和交線平行。

第三，面面平行的判定定理：一個平面內(nèi)的兩條相交直線分別平行于另一個平面，這兩個平面平行。

第四，兩個平面平行，其中一個平面內(nèi)的直線必平行于另一個平面。

第五，如果兩個平行平面同時和第三個平面相交，那么它們的交線平行。

第四和第五，均可視為面面平行的性質(zhì)定理。

對于線、面的垂直關(guān)系，有下面的網(wǎng)絡(luò)圖，如圖2。

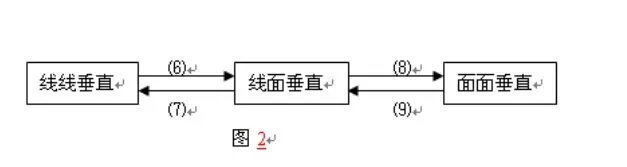
序號（6）～（9）分別代表以下判斷定理或性質(zhì)定理：

第六，線面垂直的判定定理：如果一直線和平面內(nèi)的兩相交直線垂直，這條直線就垂直于這個平面。

第七，線面垂直的性質(zhì)定理：若一直線垂直于一平面，這條直線垂直于平面內(nèi)所有直線。這條性質(zhì)實際上是由線面垂直的定義得到的。

第八，面面垂直的判定定理：一個平面經(jīng)過另一個平面的垂線，這兩個平面互相垂直。

第九，面面垂直的性質(zhì)定理：如果兩個平面垂直，那么在—個平面內(nèi)垂直于交線的直線必垂直于另—個平面。

通過以上兩個網(wǎng)絡(luò)圖，如果再進一步針對每個定理逐一畫出圖形、寫成符號語言，那么有關(guān)定理可以說基本上完成了識記這關(guān)鍵的一步。

二、重視幾個常用結(jié)論

光憑判定定理和性質(zhì)定理顯然還不足以對一些命題進行快速的判斷，我們還需掌握一些定理以外的常用結(jié)論。同樣我們可以利用下面的網(wǎng)絡(luò)圖3來幫助記憶：

序號（10）～（13）分別代表以下有用的結(jié)論：

第十，如果兩條平行線中的一條垂直于一個平面，那么另一條也垂直于這個平面。

第十一，垂直于同一個平面的兩條直線平行。

第十二，垂直于同一條直線的兩個平面平行。

第十三，一直線垂直于兩個平行平面中的一個平面，它也垂直于另一個平面。

把上述定理、常用結(jié)論（1）～（13）全部匯總到一起，就可以得到下面的網(wǎng)絡(luò)圖。

在此基礎(chǔ)上，再記住三個個關(guān)于平行的傳遞性結(jié)論。

第十四，和第三條直線都平行的兩條直線平行。

第十五，和第三個平面都平行的兩個平面平行。

第十七，平行于同一個平面的兩條直線未必平行，平行于同一條直線的兩個平面也未必平行。

三、合理使用舉反例法

對于一個假命題，往往利用舉反例的方法來判斷，會很湊效。由于舉反例法僅適用于對假命題的判斷，故要“合理使用”。

例：（2013廣東（理））設(shè)m,n是兩條不同的直線,α,β是兩個不同的平面,

下列命題中正確的是（ ）

A.若α⊥β,m?α,n?β，則m⊥n

B.若α//β,m?α,n?β，則m/ /n

C.若m⊥n,m?α,n?β,則α⊥β

D.若m⊥α,m/ /n,n/ /β, 則α⊥β

分析：用排除法，由畫圖可知選項A中m和n也可能平行，排除A，選項B中m和n也可能異面，排除B，對于選項C，宜采用舉反例法，如圖5

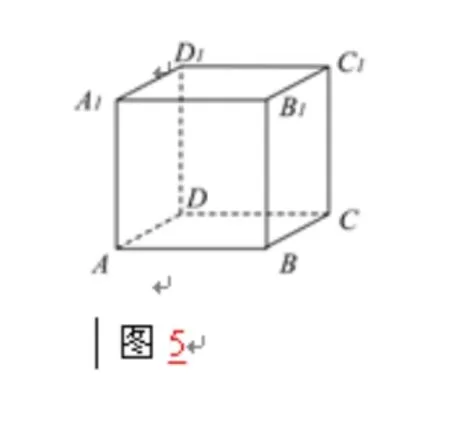
在正方體ABCD—A1B1C1D1中，A1D1?平面A1B1C1D1，BC?平面ABCD，A1D1⊥BC 但是平面A1B1C1D1與平面ABCD是平行關(guān)系，而不是垂直關(guān)系。