平拋運動與斜面結合問題的討論

寧夏銀川市第一中學 劉 丁

一、重視斜面自身的已知條件，如斜面傾角

例1：如圖所示，一個物體以v0的速度水平拋出，飛行一段時間后垂直地撞在傾角為θ的斜面上。已知重力加速度為g，不計空氣阻力。求：物體飛行的時間。

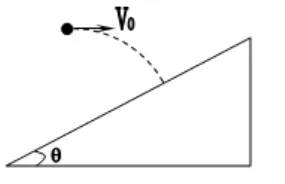
解：當小球垂直地撞在斜面上時，速度矢量圖如下圖所示

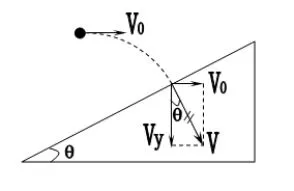
由幾何關系知：

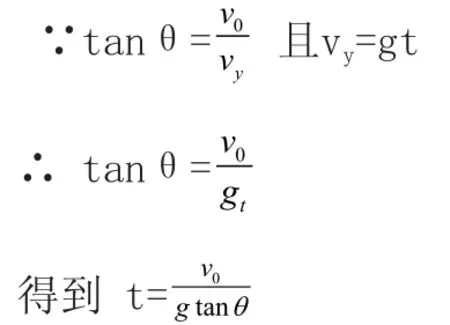
分析：此題在不知道物體做平拋運動時下落高度和水平射程的情況下求解飛行時間，只能根據“物體垂直撞在斜面上”這一條件，利用斜面傾角和速度矢量圖進行求解。由此可見，斜面傾角是一個非常關鍵的條件，所以應該提醒學生遇到此類問題要特別重視斜面的傾角。

二、在重視斜面自身已知條件的前提下，熟練應用平拋運動的規律

例2：如圖所示，一個小球以速度v1從斜面頂端水平拋出，假設斜面足夠長，當小球撞在斜面上時，其速度方向與斜面的夾角為α1。若小球以速度v2從斜面頂端水平拋出，當小球撞在斜面上時，其速度方向與斜面的夾角為α2。則α1＿α2(填“大于”“等于”或“小于”，不計空氣阻力)

解：假設斜面傾角為θ，不論小球以多大的速度從斜面頂端水平

拋出，最終撞在斜面上的速度矢量圖如下圖所示

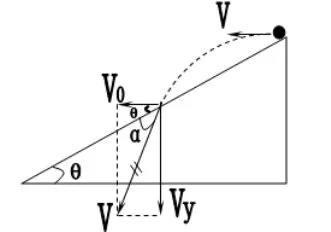
由圖可知，小球撞到斜面瞬間的速度方向與水平方向

的夾角為(α+θ)，此過程中小球的位移與水平方向的夾角為θ，

由平拋運動的規律可知

tan(a+θ) = 2tanθ

∵斜面傾角θ是一個定值，∴(α+θ)就是一個定值，則α為一個定值。因此，無論小球以多大的速度從斜面頂端水平拋出，只要又落在斜面上(斜面足夠長)，其速度方向與斜面的夾角相等，即α1=α2。

分析：這個問題又一次地告訴我們，當小球從斜面拋出，并且又落回到斜面上，則斜面的傾角是一個不容忽視的重要條件，應該想辦法利用它幫助我們解決問題。同時，熟練應用平拋運動的規律也是不可或缺的解題手段。

三、以斜面為參考系可以簡化對物體運動的分析，做到熟能生巧

例3：如圖所示，一個小球以速度v0從傾角為θ的斜面頂端水平拋出，假設斜面足夠長，已知重力加速度為g，不計空氣阻力。問：①經過多長時間小球離斜面最遠？②離斜面最遠時小球的速度是多少？方向如何？③此時距斜面的距離是多少？

解：將小球的水平初速度v0分解到垂直于斜面

和平行于斜面兩個方向上；再將重力加速度

分解到垂直于斜面和平行于斜面

兩個方向上；如下圖所示。

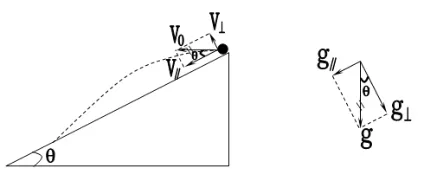
由幾何關系可得，

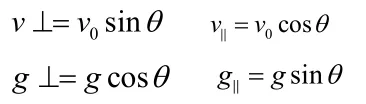
① 小球在垂直于斜面方向上先做正方向(垂直斜面向上)初速度為v0sinθ、加速度為gc osθ的勻減速直線運動，到達最高點(離斜面最遠處)后，再做反方向（垂直斜面向下）的初速度為零的勻加速度直線運動。所以，從拋出到小球離斜面最遠所需的時間為：

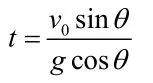
② 小球在平行于斜面方向上做初速度為v0cosθ、加速度為gs inθ的勻加速直線運動，經過t時間平行于斜面的速度為

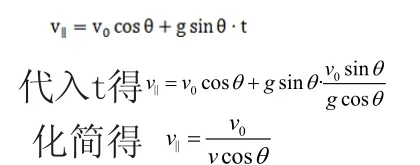
由于此時小球在垂直斜面方向上的速度為零，所以此時的合速度就等于v∥,方向沿斜面向下。

③ 當小球垂直于斜面的速度為零時，它距斜面的距離最遠，此時距離為：

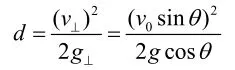
分析：從這個問題我們要獲得的方法是：一是對平拋運動進行分解時，不要以為只能分解到水平方向和豎直方向上，我們可以根據需求將它分解到任意兩個相互垂直的方向上。二是對曲線運動的研究一定要牢記合運動與分運動的等時性、獨立性等特點，根據問題將曲線運動轉化為某個方向的直線運動進行求解。

綜上所述，平拋運動與斜面結合的問題是有規律可循的，只要熟練掌握平拋運動的特點及規律、重視斜面自身的已知條件，靈活運用運動的合成與分解，就一定能找到解決問題的突破口。