在反函數法求函數值域時應注意的一個問題

文/夏金亮

在反函數法求函數值域時應注意的一個問題

文/夏金亮

對于函數值域問題的討論是初等數學中最基本也是最重要的問題。其重要之處在于這類問題研究的是函數基本概念，它與各類重要函數、反函數、函數的單調性、不等式、最值和導數等內容有著密切的聯系。對認知函數以及后面的相關內容的學習有著非凡的意義，所以求函數的值域也成為各類考試的熱門知識點。本文將對求函數值域時使用反函數法應注意的問題作出討論。

反函數法;函數;值域

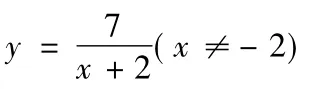
這個結果雖然正確，但是其簡答的方法卻又邏輯上的錯誤。

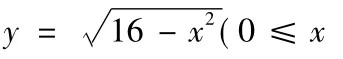
那么對于例1使用上述方法解答的結果為什么會正確呢?在什么情況下使反函數表達式有意義的一切x值的集合恰好是原函數的值域?對于這個問題，編者認為下面的定理對其作出了完整的解釋:

設函數y=f(x)的定義域A是使表達式y=f(x)有意義的一切x的值的集合，其反函數的表達式為y=g(x)，如果使表達式y= g(x)有意義的一切x值的集合為B0值域為A0，且存在g:B0→A0是一一映射，那么B0就是原函數y=f(x)的值域B。

證明:對于任意的b∈B，有a∈A，使得f(a)=b

∵f有逆映射g，故有g(b)=a，∴b∈B0，即有B?B0。

現任取b0∈B0，則存在a0使得g(b0)=a0，由于g:B0→A0是一一映射，其逆映射確定的函數應為y=f(x)，(x∈A0)，故有f(a0)=b0，其中a0∈A0，由于A是使表達式y=f(x)有意義的一切x的值的集合，∴A0?A，∴a0∈A，于是由f(a0)=b0知b0∈B

∴B?B0

綜上所述知B=B0，證畢。現在我們回頭看看前面所提到的例1，例2兩個小題:

因此對于利用反函數求函數值域這一方法必須在學生對于函數一一對應關系以及逆映射等概念有充分理解掌握的前提下進行講解，并對于那些類型函數值域求值不適合使用此反函數求值法給出例題解說。另外求原函數的反函數時，同學們往往容易出現偏差，而影響求原函數的值域，這也是要十分注意的一個問題。

由上述例題可見，在使用求反函數的定義域來求原函數的值域時，對于原函數的定義域的多樣性我們必須要有清晰的認知和理解，而準確無誤的求出原函數的反函數是使用反函數法求原函數值域的關鍵問題。

(作者單位:凱里學院)